Слайд 2
1. 曲安京.《周髀算经》新议- 陕西人民出版社, 2002. 182 c.
2. Алимов И.А., Кравцова М.Е. История

Китайской
классической литературы с древности и до ХIII в. Поэзия.
Проза. Часть первая.
«Петербургское востоковедение».СПб, 2017. 704 с.
3. http://www.wikiwand.com/en/
Ten_Computational_Canons (28.09.2017)
4. http://www.wikipedia.org
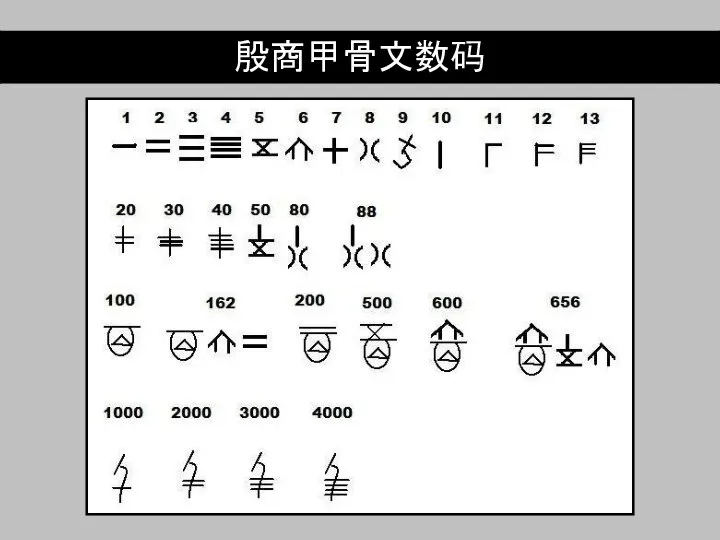
Слайд 3Цзягувэнь 甲骨文
Архаическая династия Шан-Инь «殷商»
(商朝 殷代 XVI – XI вв. до

н. э.
1600 до н. э. — 1027 до н. э.).
Население государства ~200 000 чел.
Гадальная кость цзягу 甲骨 вэнь 文 письмена
В конце XIX века кости шанской эпохи использовались в традиционной китайской медицине как снадобье от малярии и ножевых ранений.
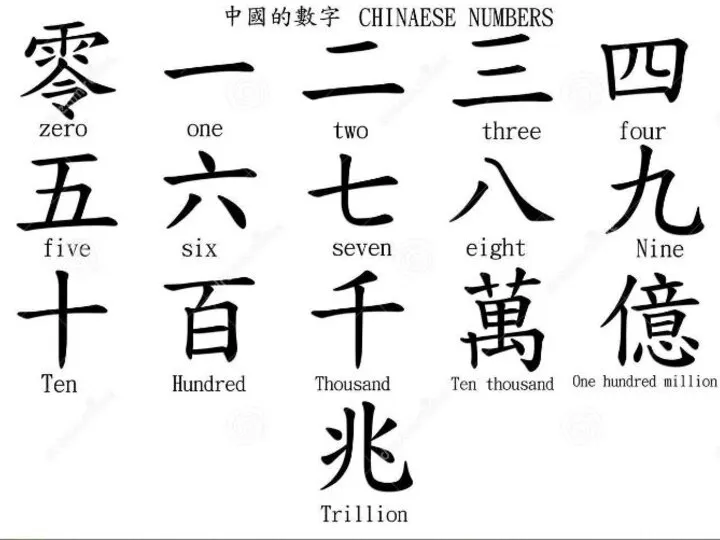
Слайд 9«Куриальное начертание»
Ноль – 零
一 - 壹 – yī
二 - 貳

– èr
三 - 參 – sān
四 - 肆 – sì
五 - 伍 – wǔ
六 - 陸 – liù
七 - 柒 – qī
八 - 捌 – bā
九 - 玖 – jiǔ
十 - 拾 – shí
万 - 萬 – wàn
大寫 dàxiě
Слайд 10«Куриальное начертание»
The parenthesized entries are the complex and formal forms,

which are used mainly
in notarized, official documents, and when writing checks.
An exception is zero; the complex form is much more widely
used than a casual circle.
The complex forms are known in English as banker's anti-fraud numerals,
in Chinese as 大寫 dàxiě (which is the same term for "capital letter").
They are necessary because, since normal
Chinese characters are so simple,
a forger could easily change 三十 to 五千 with just three strokes.
See Standard numbers for more information.
Слайд 11Чжан Хэн 張衡 (公元78年-139年)
Великий учёный и изобретатель
Рассчитал
π (юань чжоу люй

圓周率):
1. 92/29 ≈ 3,1724
2. Корень из 10 ≈ 3,1622
Слайд 12Лю Хуэй 劉徽 (公元225年-295年)
Жил в эпоху Троецарствия
(Саньго三國 220-280)
Цао Вэй 曹魏
劉徽

Лю Хуэй редактор-комментатор издания:
Цзючжан суаньшу 九章算術 (公元 263 年)
«Математика в девяти книгах»
246 задач
Напр.
Лю Хуэй 刘徽 Цзючжан суаньшу 九章算术
Ишу Чжунго ван 艺术中国网, 1985.198 с.
Слайд 13Цзючжан суаньшу 九章算術
Цзючжан суаньшу 九章算術
«Математика в девяти книгах»
246 задач
Напр.
粟米 Су ми «Соотношение злаков» —

Правила обмена и торговли
衰分 Шуай фэнь, «Деление по ступеням» —
Пропорциональное распределение товара.
廣 Шао гуан — Теория делимости.
Извлечение квадратных и кубических корней.
Измерение круга, сферы и шара.
商功 Шан гун, «Оценка работ» — Объёмы различных
тел: параллелепипед, призма, пирамида, цилиндр, конус.
Расчёт трудозатрат при строительстве.
勾股 Гоу гу — Теорема Пифагора
И др.
Слайд 14Лю Хуэй 劉徽 (公元225年-295年)
Расчёт числа π методом вписанных правильных многоугольников.
Решение систем линейных уравнений методом, названным впоследствии именем

Гаусса.
Расчёт объёма призмы, пирамиды, тетраэдра, цилиндра, конуса и усечённого конуса; метод неделимых.
Слайд 15Цзу Чунчжи 祖沖之 (公元429年-500年)
Китайский математик
и астроном.
Начальник уезда

Слайд 16Цзу Чунчжи 祖沖之 (公元429年-500年)
Расчитал продолжительность года в
365.24281481 дней
(сейчас подсчитана 365.24219878 дней)

Слайд 17Цзу Чунчжи 祖沖之 (公元429年-500年)
Ми люй 密率«Приближённое значение»
π (юань чжоу люй 圓周率)
355/113

Слайд 18Цзу Чунчжи 祖沖之 (公元429年-500年)
Юэ люй 約率 «Примерное значение»
π (юань чжоу люй

圓周率)
22/7
Слайд 19Ли Чуньфэн 李淳风 (公元602年- 670年)
Редактор-компилятор
«Десяти математических канонов»
Входивших в библиографический

список для подготовки к государственному экзамену (кэцзюй 科舉)
В эпоху Тан
Слайд 20Ли Чуньфэн (李淳风 602 - 670)
«Десять
математических
канонов»

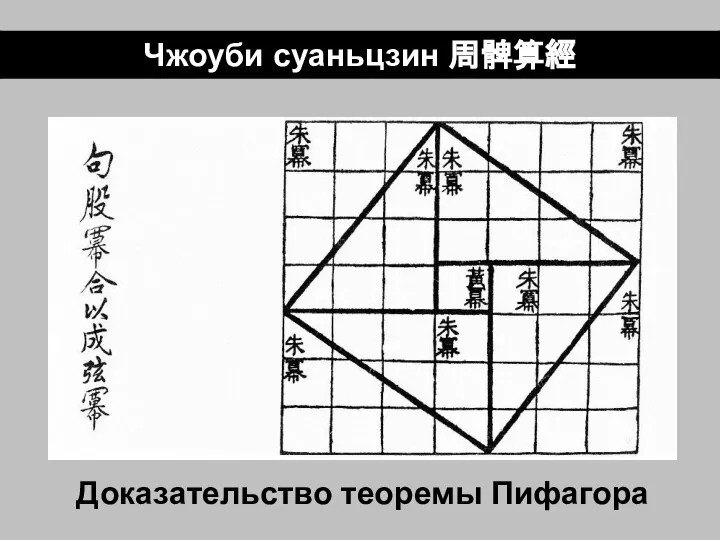
Слайд 21Чжоуби суаньцзин 周髀算經
Труд создан в эпоху Чжоу ((周) 1046-771 д.н.э.)

246 вопросов, обсуждавшихся Чжоу Гуном 周公
и его придворным астрономом
Включает в себя одно из первых доказательств
теоремы Пифагора
Описание астрономических наблюдений
Слайд 22Доказательство теоремы Пифагора
«Десять
математических
канонов»
Слайд 23
Доказательство теоремы Пифагора
Издание 1603 г. «10 математических канонов»
(копия Чжоуби суаньцзин 100

г. д.н.э.)
Слайд 24Цзючжан суаньшу 九章算术
«Девять глав математического искусства»
Компиляция трудов X-II в. д.н.э.
Постановка

вопроса
Формулировка ответа,
обьяснение процедуры поиска ответа на
[математический] вопрос
Слайд 25Чжоуби суаньцзин 周髀算經
Прочие трактаты из
«Десяти математических канонов»:
Хайдао суаньцзин 海岛算经
Суньцзы суаньцзин 孙子算经
Цзигу

суаньцзин Суньцзы суаньццзин 孙子算经
И т.п.
Слайд 26ЭКЗАМЕН Кэцзюй 科舉 (эпоха Тан)
На изучение каждого из 10 трактатов
Полагалось

по одному году, иногда по два года и более,
Затем изучивший каждый трактат пробовал сдать экзамен
Несдавшие экзамен оказывались на улице,
и без денег могли стать лишь
даосскими-монахами отшельниками либо «разнорабочими»
Либо искали покровительства (и возможно любви и денег)
у знатных чиновников























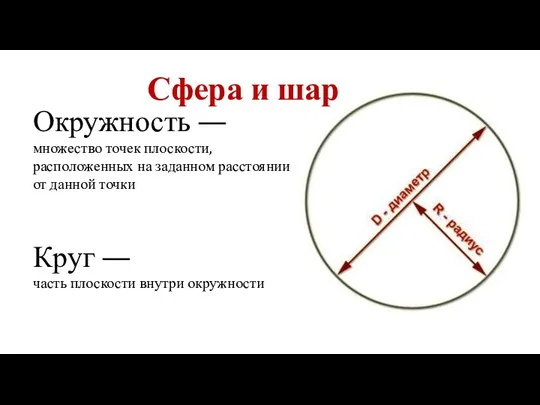 Сфера и шар
Сфера и шар Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ  Деление. Неправильные дроби
Деление. Неправильные дроби Геометрия в живописи
Геометрия в живописи Угол между прямой и плоскостью
Угол между прямой и плоскостью Задачи на прогрессию
Задачи на прогрессию Поверхностные интегралы первого рода
Поверхностные интегралы первого рода Степенная функция
Степенная функция Уравнение Бернулли
Уравнение Бернулли Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Площадь поверхности цилиндра
Площадь поверхности цилиндра Параллельные прямые
Параллельные прямые Ромб. Решение 6 задачи
Ромб. Решение 6 задачи Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики B7
B7 Презентация на тему Принцип Дирихле
Презентация на тему Принцип Дирихле  Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2)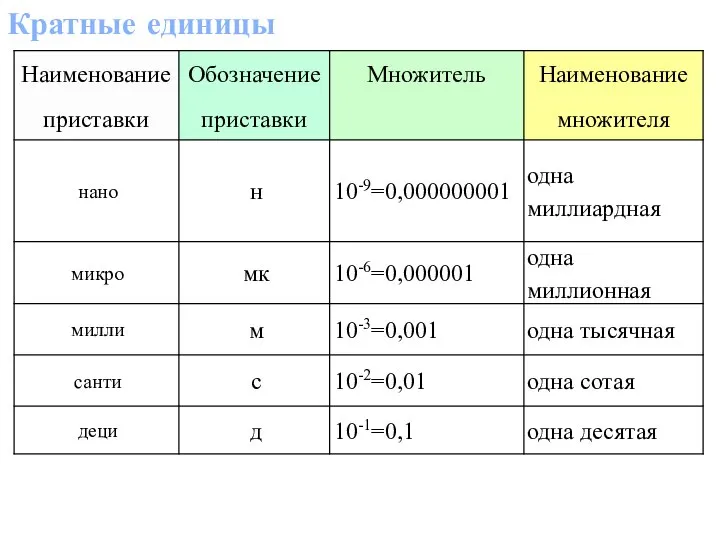 Кратные единицы
Кратные единицы Алгебра. Задачник, часть 2
Алгебра. Задачник, часть 2 Треугольники, задача
Треугольники, задача Прямоугольник
Прямоугольник Устный счёт. Для 5 коррекционного класса VIII вида
Устный счёт. Для 5 коррекционного класса VIII вида Олимпиадная математика. Доказательство от противного
Олимпиадная математика. Доказательство от противного Естественно балансирующееся общество
Естественно балансирующееся общество ریاضی جزوه کامل
ریاضی جزوه کامل Таблица Шульте
Таблица Шульте Понятие производной
Понятие производной Почти все об углах
Почти все об углах