Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью

Виды рядов динамики и задачи, решаемые с их помощью.
Базисные и цепные показатели динамики.
Средние уровни и показатели динамики.
Выявление основной тенденции развития социально-экономических явлений.
Вопросы лекции

Виды рядов динамики и задачи, решаемые с их помощью.

Определение ряда динамики
Ряд динамики – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени

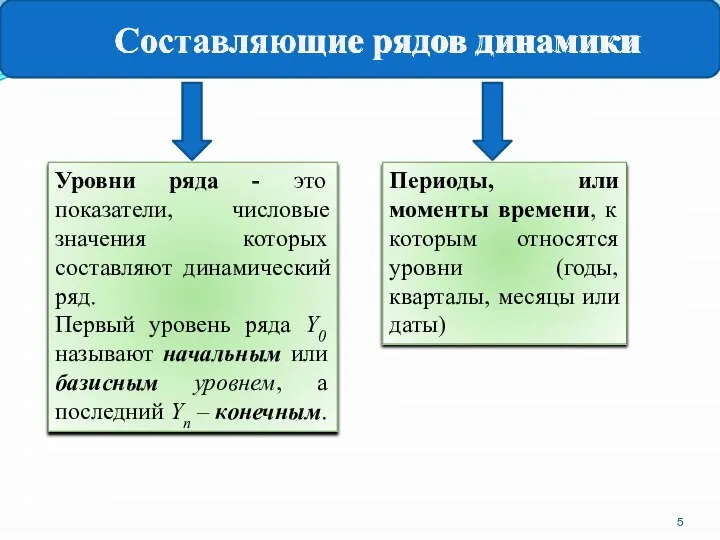
Составляющие рядов динамики
Уровни ряда - это показатели, числовые значения которых составляют динамический ряд.
Первый уровень ряда Y0 называют начальным или базисным уровнем, а последний Yn – конечным.
Периоды, или моменты времени, к которым относятся уровни (годы, кварталы, месяцы или даты)

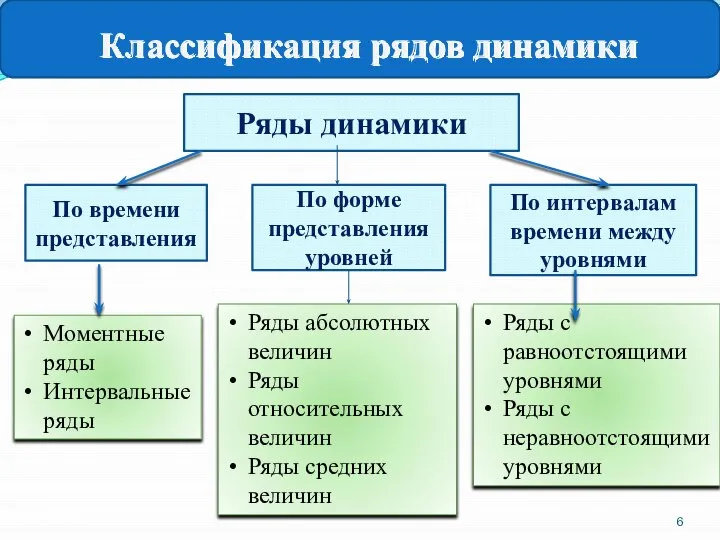
ВЫДЫ СРЕДНИХ ПОКАЗАТЕЛЕЙ
Ряды динамики
По времени представления
По интервалам времени между уровнями
Моментные ряды
Интервальные ряды
Ряды с равноотстоящими уровнями
Ряды с неравноотстоящими уровнями
Классификация рядов динамики
По форме представления уровней
Ряды абсолютных величин
Ряды относительных величин
Ряды средних величин

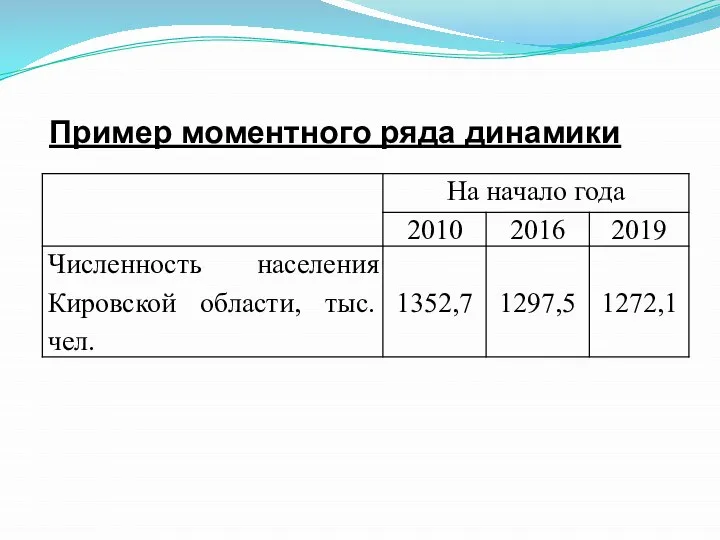
Моментным называется ряд динамики уровни которого характеризуют состояние каких-либо явлений на определенный момент времени, (на начало года, конец года, квартала, месяца.)

Пример моментного ряда динамики

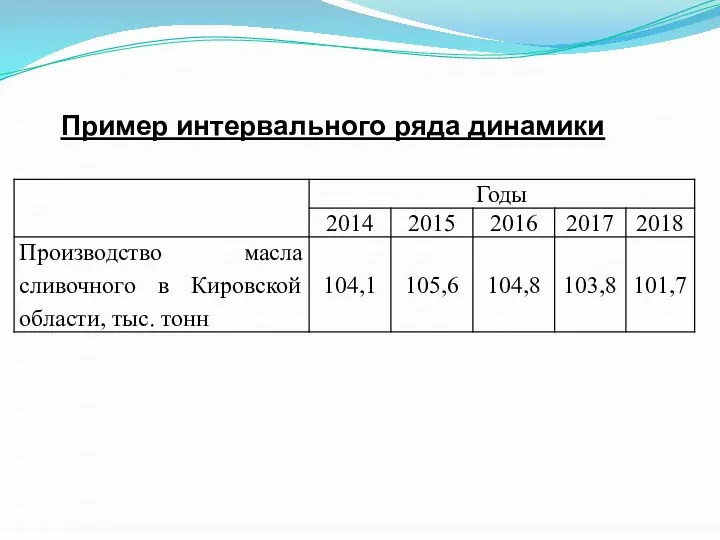
Интервальным рядом динамики называется такой ряд, уровни которого характеризуют размеры явлений за определенный промежуток времени. Они отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.

Пример интервального ряда динамики

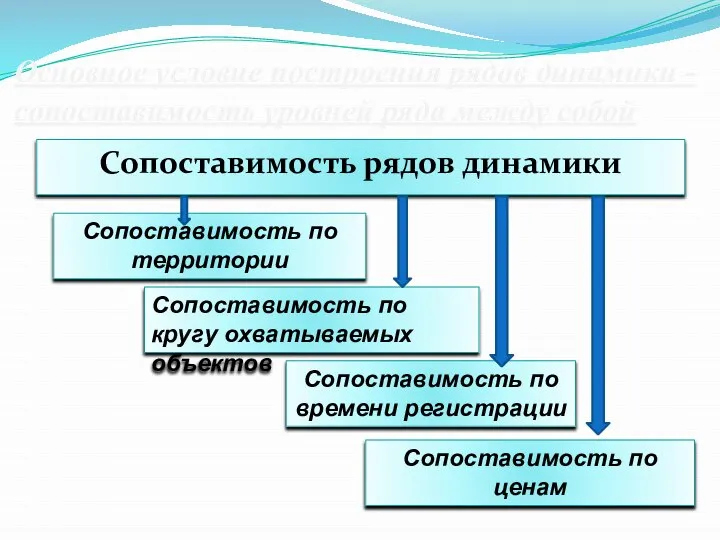
Основное условие построения рядов динамики - сопоставимость уровней ряда между собой
Сопоставимость рядов динамики
Сопоставимость по кругу охватываемых объектов
Сопоставимость по времени регистрации
Сопоставимость по ценам
Сопоставимость по территории

Статистическое изучение динамики социально-экономических явлений позволяет решать следующие основные задачи:
1)измерить скорость изменения уровней за определенный промежуток времени;
2)выявить и численно характеризовать основные тенденции развития изучаемых явлений во времени;
3)выявить факторы, обуславливающие такие изменения;
4)определить прогнозы развития явления в будущем.

2.Базисные и цепные показатели динамика.

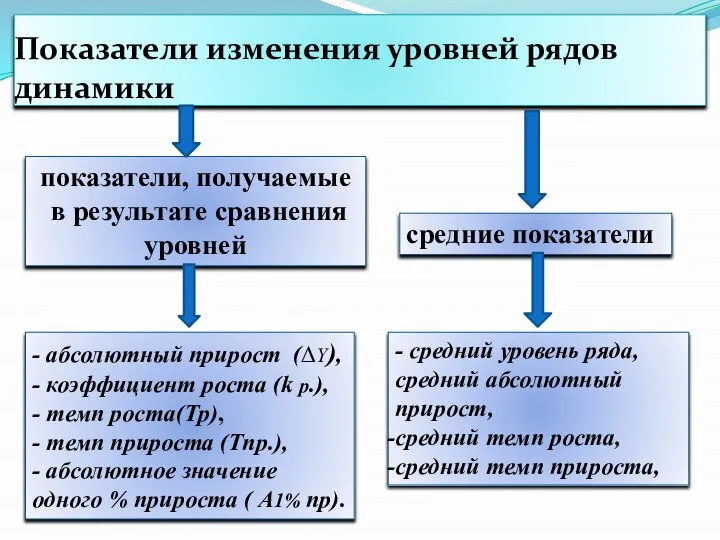
Показатели изменения уровней рядов динамики
показатели, получаемые
в результате сравнения уровней
средние показатели
- абсолютный прирост (∆Y),
- коэффициент роста (k р.),
- темп роста(Tр),
- темп прироста (Тпр.),
- абсолютное значение одного % прироста ( A1% пр).
- средний уровень ряда,
средний абсолютный прирост,
средний темп роста,
средний темп прироста,

Для характеристики изменения уровней ряда динамики во времени определяют систему базисных и цепных показателей.
Базисные показатели определяют при сравнении каждого последующего уровня ряда с принятым за базу (обычно начальным) уровнем. При расчете цепных показателей каждый последующий уровень сравнивают с предыдущим.

1.Абсолютный прирост (сокращение)(∆Y) – это разность между двумя сравниваемыми уровнями. Он показывает, на сколько сравниваемый уровень больше (меньше) по сравнению с предыдущим, или базисным.

Где: Yi - уровень сравниваемого периода;
Yi-1 - уровень предшествующего периода.
Абсолютный прирост (цепной)
∆Y ц = Yi - Yi-1
Абсолютный прирост
(базисный)
∆Y б = Yi - Y0
Y0 - уровень базисного периода

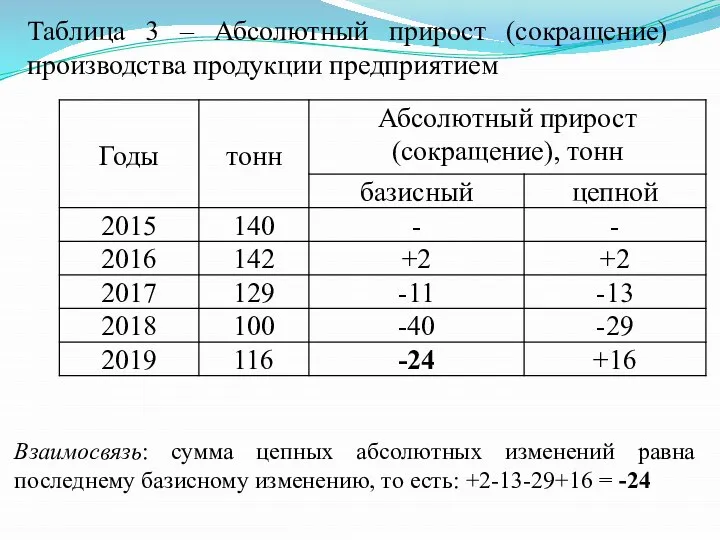
Взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть: +2-13-29+16 = -24
Таблица 3 – Абсолютный прирост (сокращение) производства продукции предприятием

2.Темп и коэффициент роста (снижения)
Коэффициент роста представляет собой кратное отношение сравниваемого уровня к предыдущему или базисному.

Темп роста (снижения)– это отношение сравниваемого уровня к предыдущему, или базисному, выраженное в %. Его можно также определить путем умножения коэффициента роста на 100%.

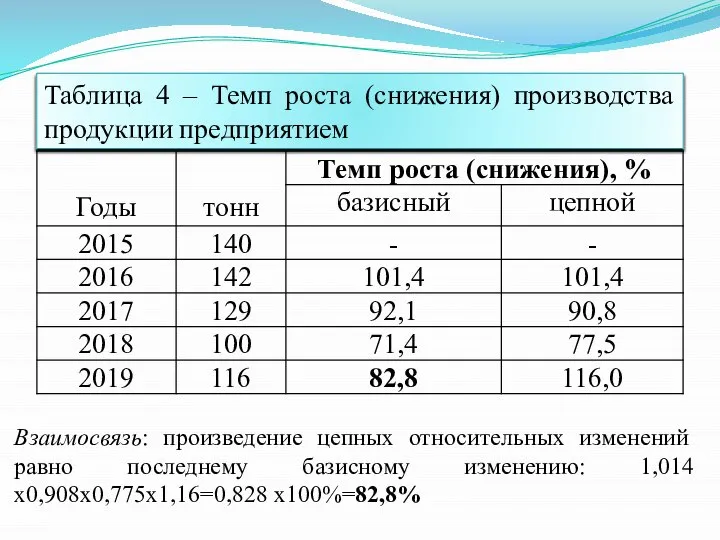
Взаимосвязь: произведение цепных относительных изменений равно последнему базисному изменению: 1,014х0,908х0,775х1,16=0,828 х100%=82,8%
Таблица 4 – Темп роста (снижения) производства продукции предприятием

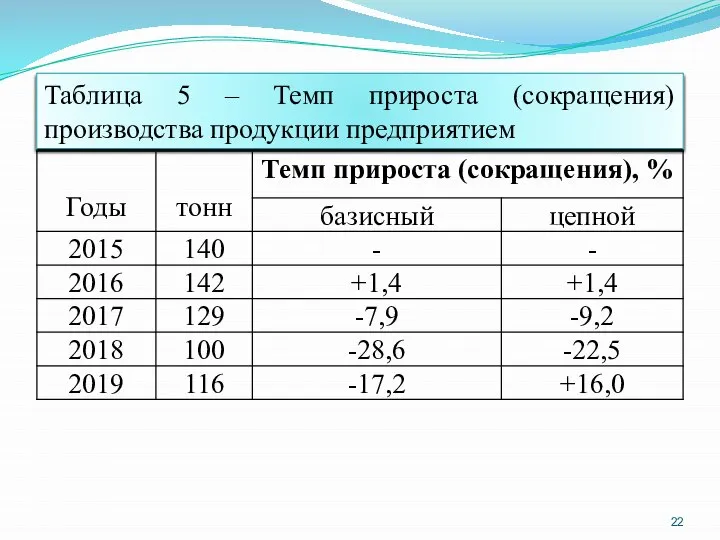
3. Темп прироста (сокращения) показывает, на сколько % сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к уровню предыдущему или базисному.
Этот показатель можно также определить путем вычитания 100% из темпа роста:
Тприр.=Тр.-100%

22
Таблица 5 – Темп прироста (сокращения) производства продукции предприятием

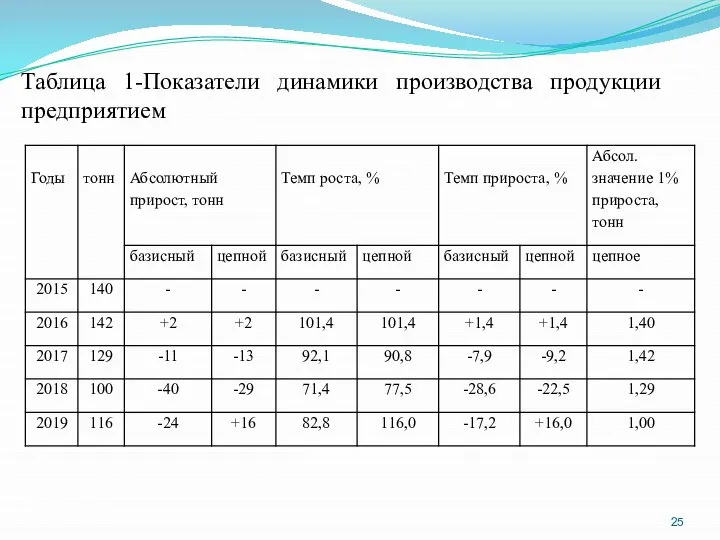
4. Абсолютное значение одного процента прироста
(∆1%) представляет собой и отношение абсолютного прироста к соответствующему темпу роста.
Данный показатель рассчитывают по формуле

Таблица 1-Показатели динамики производства продукции предприятием

3.Средние уровни и показатели динамики.

Средний уровень интервального ряда динамики с равными интервалами определяется по формуле средней арифметической простой:
п- число уровней ряда.

Средний уровень моментного ряда динамики определяется по формуле средней хронологической:
.

Средний абсолютный прирост определяется по формуле:
Среднегодовой абсолютный прирост составит:
(по данным таблиц 3 – 5)

Средний темп роста определяется:
.
Или, используется формула средней геометрической:
Где Т1, Т2,… Тт –цепные темпы роста; m - число темпов.

Среднегодовой темп роста будет равен
(по данным таблиц 3 – 5):
.
Среднегодовой темп прироста:

4.Выявление основной тенденции развития социально-экономических явлений.

Для выявления основной тенденции, т.е. закономерности изменения уровней динамического ряда, используются различные способы выравнивания, или сглаживания уровней.
Сущность различных приемов выравнивания сводится к замене фактических уровней временного ряда расчетными, в меньшей степени подверженными случайным колебаниям.

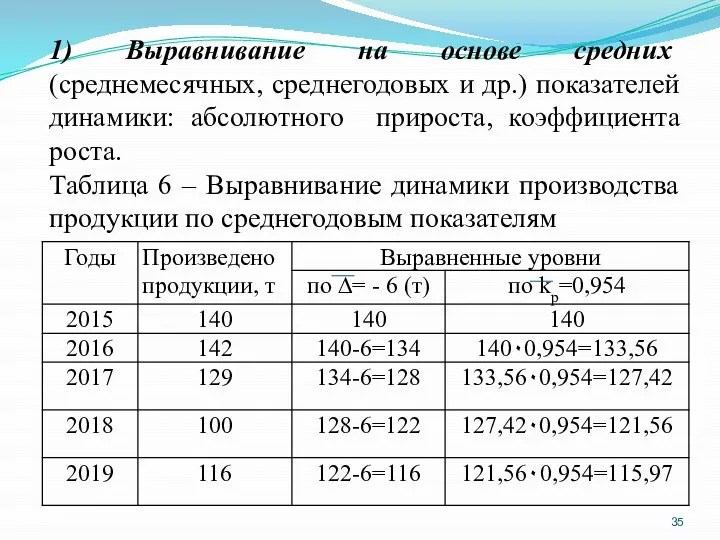
1) Выравнивание на основе средних (среднемесячных, среднегодовых и др.) показателей динамики: абсолютного прироста, коэффициента роста.
Таблица 6 – Выравнивание динамики производства продукции по среднегодовым показателям

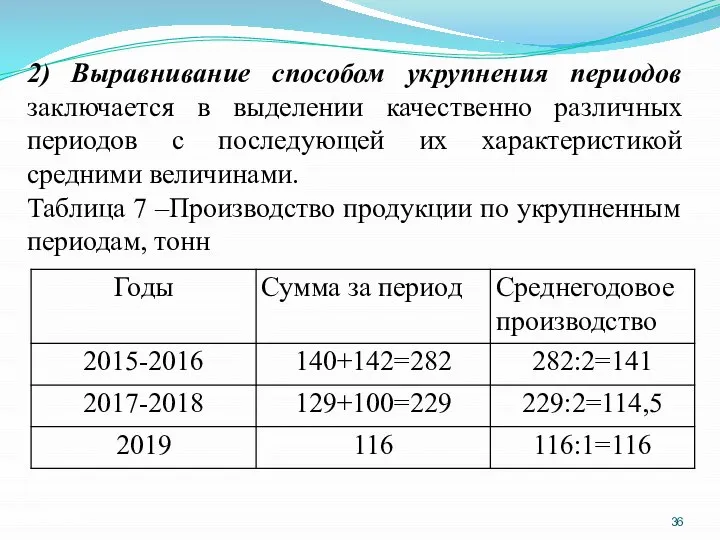
2) Выравнивание способом укрупнения периодов заключается в выделении качественно различных периодов с последующей их характеристикой средними величинами.
Таблица 7 –Производство продукции по укрупненным периодам, тонн

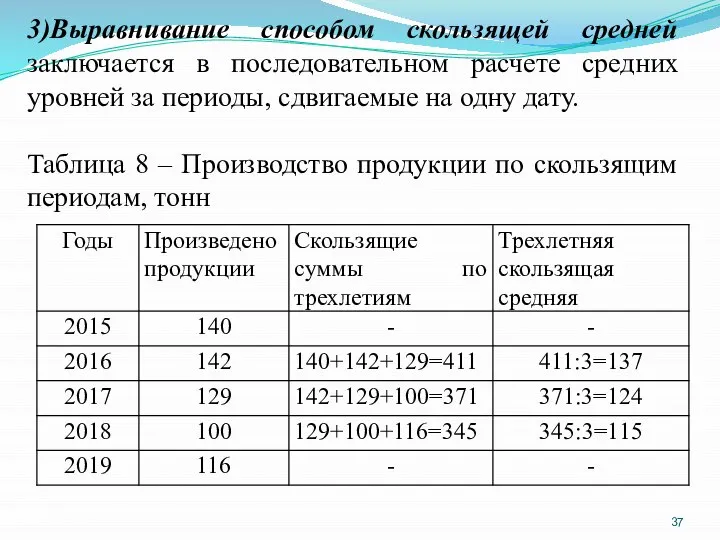
3)Выравнивание способом скользящей средней заключается в последовательном расчете средних уровней за периоды, сдвигаемые на одну дату.
Таблица 8 – Производство продукции по скользящим периодам, тонн

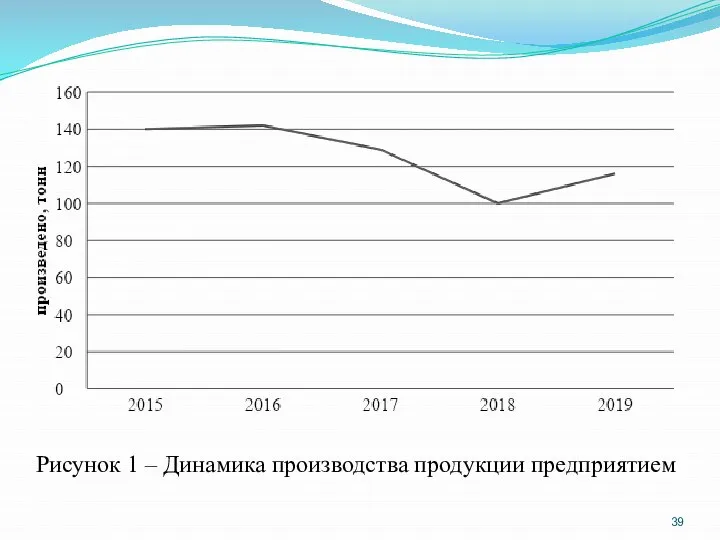
Рисунок 1 – Динамика производства продукции предприятием

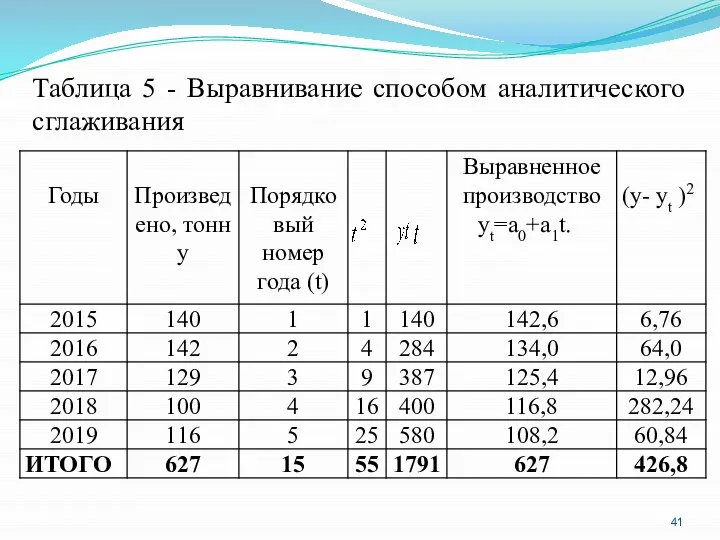
Таблица 5 - Выравнивание способом аналитического сглаживания

Для оценки степени приближения выравненных уровней к исходным определяют величину остаточного среднего квадратического отклонения.
Следовательно, выравненные уровни отклоняются от исходных в среднем на 9,2 тонны, что составляет 7,3% относительно среднего уровня ряда, равного 125,4 тонны (627:5=125,4).

Анализ сезонных колебаний.
Сезонные колебания – это регулярно повторяющиеся подъемы и снижения уровней ряда динамики на протяжении ряда лет.
Сезонность имеет место в различных отраслях экономики: в торговле, сельском хозяйстве, строительстве, транспорте и других.
Сезонность в изменении явлений можно наглядно представить на графике, построив сезонную волну.

Количественная оценка сезонности может быть дана при помощи индекса сезонности. Он равен отношению среднего уровня для каждого месяца, или квартала по данным за последние 2-3 года к общему среднемесячному, или среднеквартальному уровню

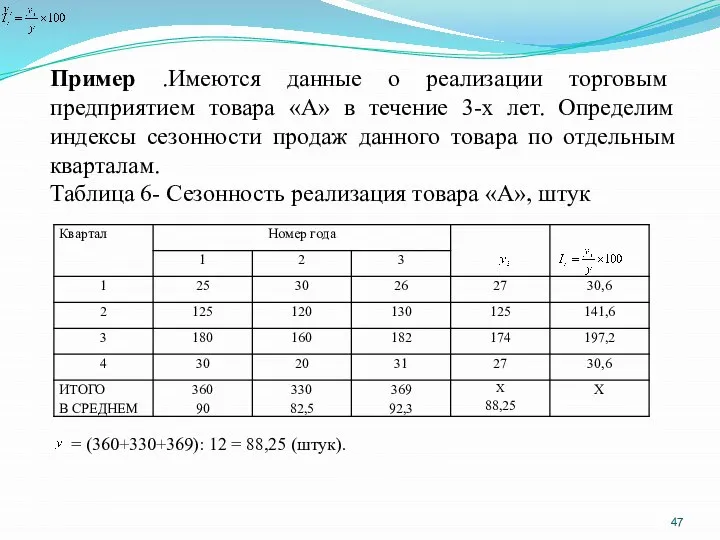
Пример .Имеются данные о реализации торговым предприятием товара «А» в течение 3-х лет. Определим индексы сезонности продаж данного товара по отдельным кварталам.
Таблица 6- Сезонность реализация товара «А», штук
= (360+330+369): 12 = 88,25 (штук).