Содержание
- 2. Содержание Что такое матрица? Карл Фридих Гаусс Метод Гаусса Габриэль Крамер Метод Крамера Вывод Использованные источники
- 3. Матрица Определение Прямоугольная таблица из m, n чисел, содержащая m – строк и n – столбцов,
- 4. Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген) Биография Дед Гаусса
- 5. Метод Гаусса Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения
- 6. Типы уравнений Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не
- 7. Элементарные преобразования К элементарным преобразованиям системы отнесем следующее: перемена местами двух любых уравнений; умножение обеих частей
- 8. Общий случай Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в
- 9. 2-ой шаг метода Гаусса На втором шаге исключим неизвестное х2 из третьего уравнения системы (3). Пусть
- 10. В результате преобразований система приняла вид: Система вида (5) называется треугольной. Процесс приведения системы (1) к
- 11. Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b ≠ 0,
- 12. Рассмотрим на примере Покажем последовательность решения системы из трех уравнений методом Гаусса Поделим первое уравнение на
- 13. Метод Крамера Метод Крамера—способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём
- 14. Габриэль Крамер (31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция) Биография Крамер родился в семье
- 15. Рассмотрим систему линейных уравнений с квадратной матрицей A , т.е. такую, у которой число уравнений совпадает
- 16. Имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: a11
- 17. В этом случае решение можно вычислить по формуле Крамера
- 18. Для получения значения xk в числитель ставится определитель, получающийся из det(A) заменой его k-го столбца на
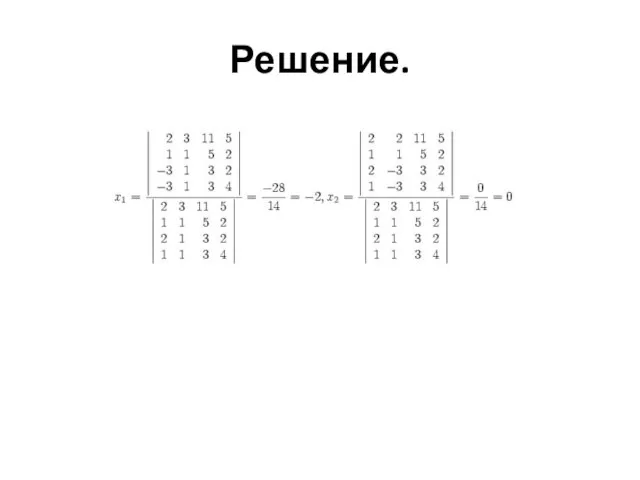
- 19. Решение.
- 20. Найдите оставшиеся компоненты решения. Формулы Крамера не представляют практического значения в случае систем с числовыми коэффициентами:
- 21. Найдите оставшиеся компоненты решения. Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса
- 22. Решение. В этом примере определитель матрицы системы равен . По теореме Крамера система совместна при .
- 23. Ответ. Приведенный пример поясняет также каким образом система линейных уравнений, непрерывно зависящая от параметра, становится несовместной:
- 24. Вывод Рассмотренный в данной презентации Метод Крамера позволяет решать линейные системы, но удобнее решать системы линейных
- 26. Скачать презентацию






















 Теория игр
Теория игр Диагонали квадрата
Диагонали квадрата Переменные величины и их свойства
Переменные величины и их свойства Решение задач
Решение задач Сечения многогранников
Сечения многогранников Презентация на тему Основные тригонометрические формулы
Презентация на тему Основные тригонометрические формулы  Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии Элементы линейной алгебры. Матрицы. Определители
Элементы линейной алгебры. Матрицы. Определители Презентация на тему Раскрытие скобок (5 класс)
Презентация на тему Раскрытие скобок (5 класс)  Решение иррациональных уравнений
Решение иррациональных уравнений Теория вероятностей. Вычисление вероятности выигрыша
Теория вероятностей. Вычисление вероятности выигрыша Канонические поверхности 2-го порядка
Канонические поверхности 2-го порядка Математическое моделирование и оптимальное управление каталитическими процессами в условиях неопределенности
Математическое моделирование и оптимальное управление каталитическими процессами в условиях неопределенности Лекция+1+-+Предел+числовой+последовательности
Лекция+1+-+Предел+числовой+последовательности Проекция вершин, ребер и граней
Проекция вершин, ребер и граней Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Скалярное прозведение векторов
Скалярное прозведение векторов Алгебраические и геометрические модели
Алгебраические и геометрические модели Нормальные формы булевых функций
Нормальные формы булевых функций Презентация на тему Свойства и график функции синус
Презентация на тему Свойства и график функции синус  Обыкновенные дроби
Обыкновенные дроби Линейные неравенства с параметром
Линейные неравенства с параметром Многогранники. Решение задач
Многогранники. Решение задач Презентация по математике "Дроби на Руси" -
Презентация по математике "Дроби на Руси" -  Производная вокруг нас
Производная вокруг нас Основатели теории вероятности и её значение на практике
Основатели теории вероятности и её значение на практике Треугольники. Часть 1
Треугольники. Часть 1