Содержание
- 2. Задание: Выполнить действия
- 3. Решение:
- 4. В теорию: Определение ТОЖДЕСТВОМ НАЗЫВАЕТСЯ РАВЕНСТВО, ВЕРНОЕ ПРИ ЛЮБЫХ ДОПУСТИМЫХ ЗНАЧЕНИЯХ ПЕРЕМЕННЫХ. 31.01.2022г.
- 5. ПРИМЕРЫ ТОЖДЕСТВ: a+b=b+a a+(b+c)=(a+b)+c ab=ba a(bc)=(ab)c a(b+c)=ab+ac a+0=a a∙0=0 a∙1=a a∙(-1)=-a
- 6. Запомним:
- 7. В теорию: Способы доказательства тождеств: Преобразование левой части тождества так, чтобы получилась её правая часть (если
- 8. Решение. Преобразуем левую часть равенства: а(в - х) + х(а + в) = = ав –
- 9. В теорию (способы доказательства тождеств): 2. Преобразование правой части тождества так, чтобы получилась её левая часть
- 10. В теорию (способы доказательства тождеств): 3. Преобразование обеих частей тождества…(должны получится одинаковые выражения) Докажите тождество: Упростим
- 11. В теорию (способы доказательства тождеств): 4. Найти разность между правой и левой частями выражения. (если эта
- 13. Скачать презентацию
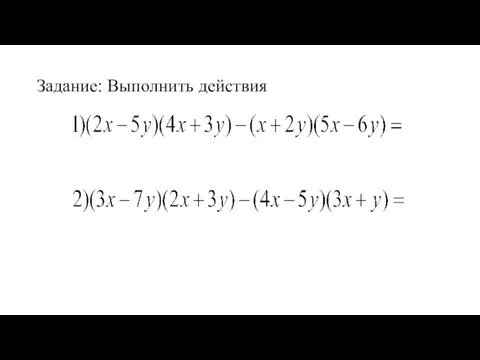









 Знакомство с подсчётом вероятности
Знакомство с подсчётом вероятности Тест. Равенство треугольников
Тест. Равенство треугольников Логарифм числа
Логарифм числа Презентация по математике "Сложение и вычитание в пределах 1000" -
Презентация по математике "Сложение и вычитание в пределах 1000" -  Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ  Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Сложение с числом 10
Сложение с числом 10 Линейная корреляция
Линейная корреляция Проецирование – это процесс получения
Проецирование – это процесс получения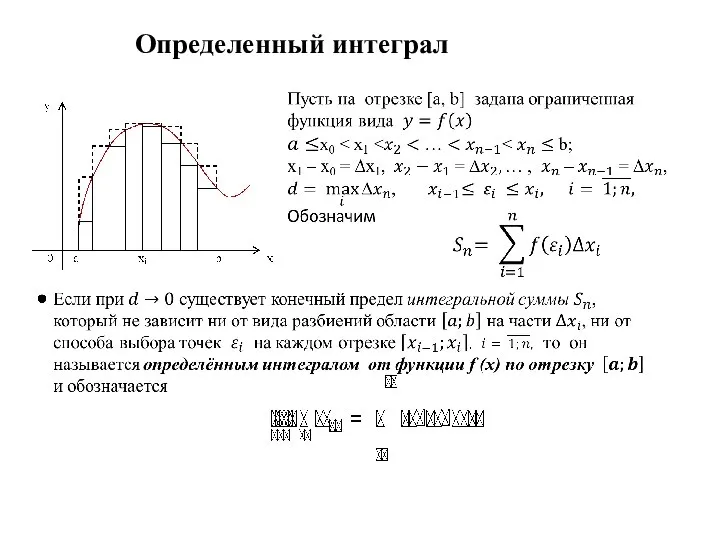 Определённый интеграл
Определённый интеграл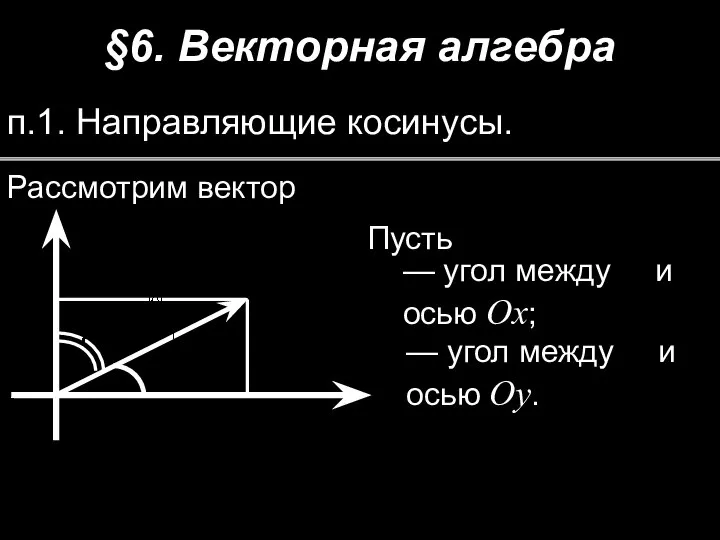 2.3. Векторная алгебра
2.3. Векторная алгебра Признаки параллельности прямых
Признаки параллельности прямых Решение задач. Урок математики
Решение задач. Урок математики Сложение вида + 1, вычитание вида -1
Сложение вида + 1, вычитание вида -1 Подготовка к ЕГЭ
Подготовка к ЕГЭ Цифры - прописи. Анимированный плакат
Цифры - прописи. Анимированный плакат Лекция 5. Трехмерные преобразования
Лекция 5. Трехмерные преобразования Кратные чисел. 5 класс
Кратные чисел. 5 класс 2020.09.03 Десятичная система записи натуральных чисел
2020.09.03 Десятичная система записи натуральных чисел Pervoobraznaya
Pervoobraznaya Итоговой тест по геометрии. 9 класс
Итоговой тест по геометрии. 9 класс Приведение уравнений фигур к каноническому виду при помощи квадратичных форм
Приведение уравнений фигур к каноническому виду при помощи квадратичных форм Решение треугольников
Решение треугольников Треугольник. Виды треугольников
Треугольник. Виды треугольников Моделирование вероятности столкновения судов
Моделирование вероятности столкновения судов Сплайн интерполяция. Отчёт по домашней работе №3
Сплайн интерполяция. Отчёт по домашней работе №3 Иррациональные числа
Иррациональные числа Тест 3 по математике
Тест 3 по математике