Содержание
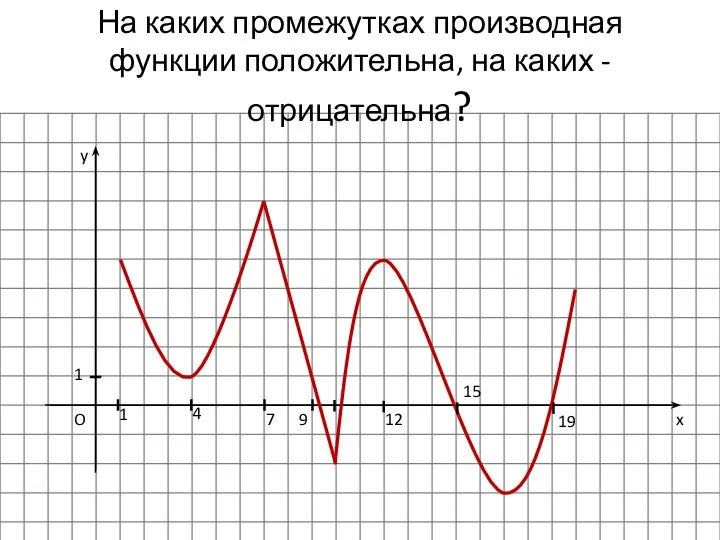
- 2. x y O 1 1 4 7 9 12 15 19 На каких промежутках производная функции
- 3. Что можно сказать об угловом коэффициенте касательной к графику функции, если известно, что функция: а) возрастает;
- 4. Найти промежутки возрастания и убывания функции
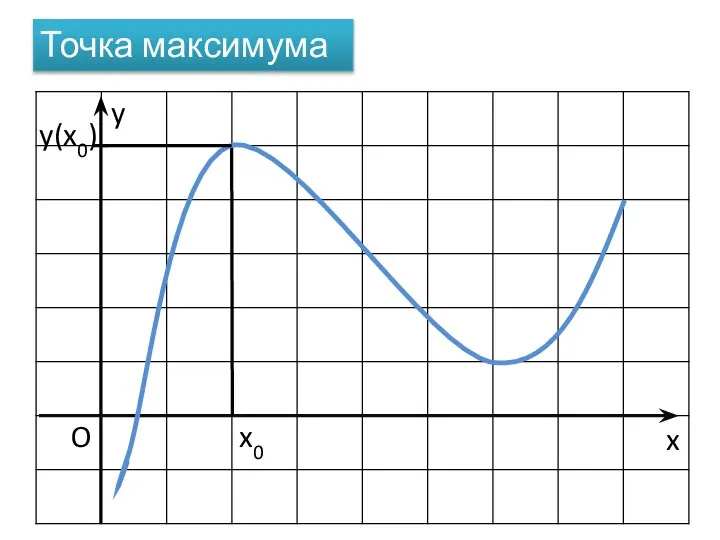
- 5. x O x0 Точка максимума y(x0) y
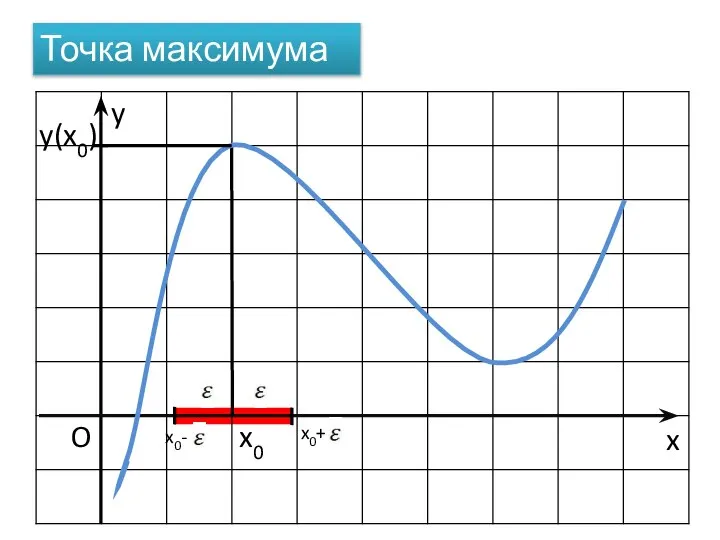
- 6. x O x0 Точка максимума x0+ x0- y y(x0)
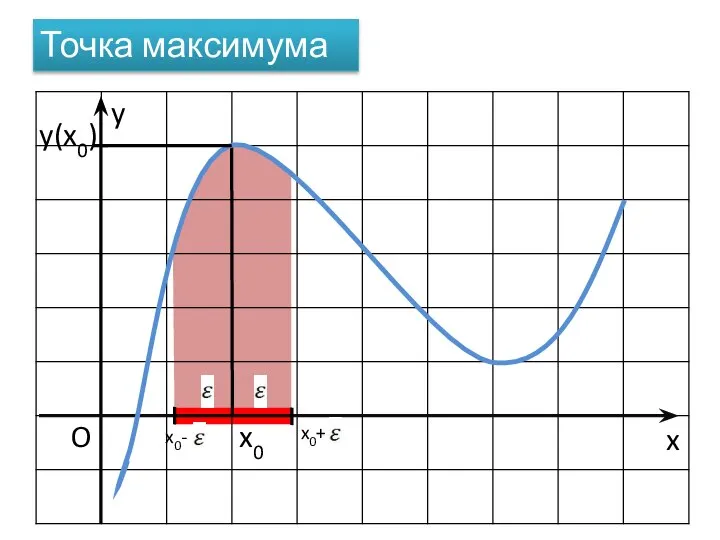
- 7. x O x0 Точка максимума x0+ x0- y y(x0)
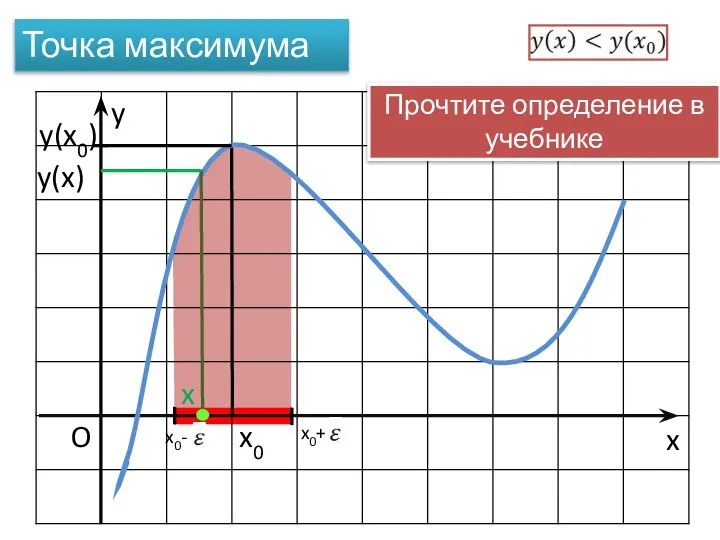
- 8. x y O x0 Точка максимума x0+ x0- x y(x0) y(x) Прочтите определение в учебнике
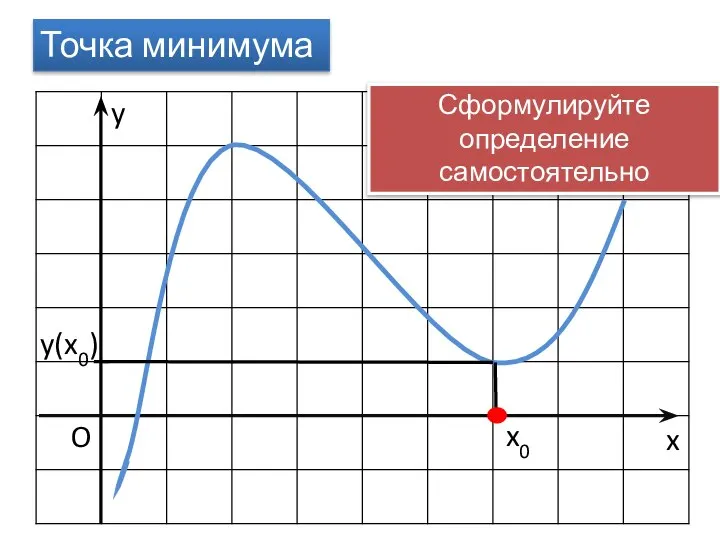
- 9. x O x0 Точка минимума y(x0) y Сформулируйте определение самостоятельно
- 10. Точки максимума и минимума называются точками экстремума функции
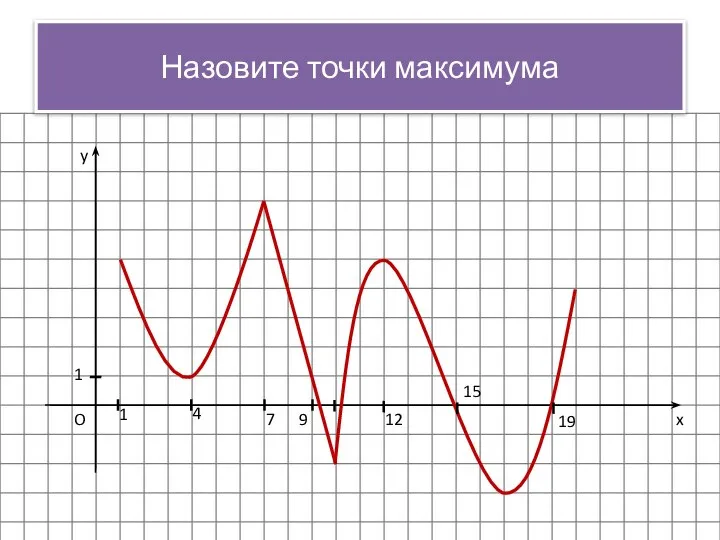
- 11. x y O 1 1 4 7 9 12 15 19 Назовите точки максимума
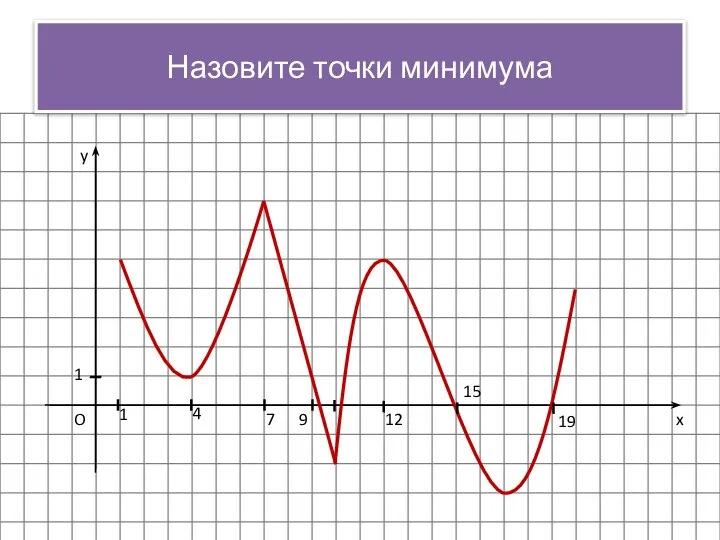
- 12. x y O 1 1 4 7 9 12 15 19 Назовите точки минимума
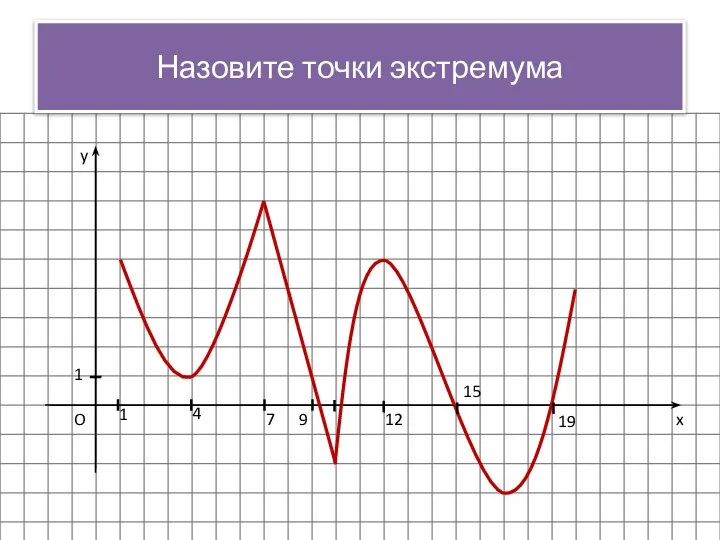
- 13. x y O 1 1 4 7 9 12 15 19 Назовите точки экстремума
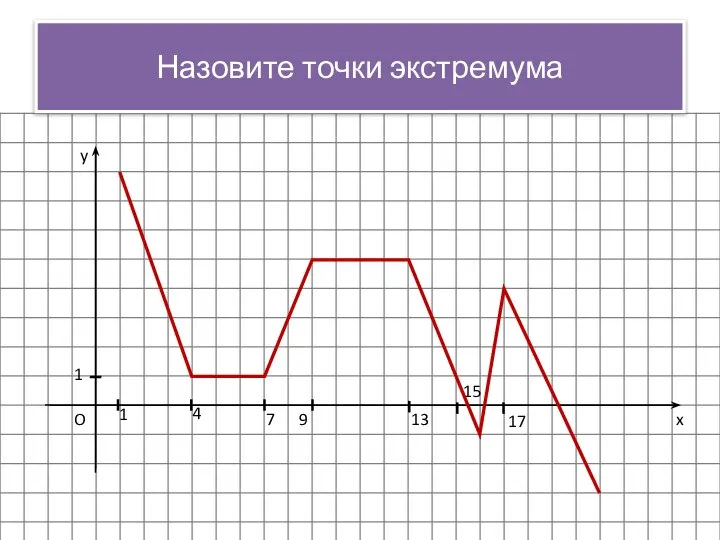
- 14. x y O 1 1 4 7 9 13 15 17 Назовите точки экстремума
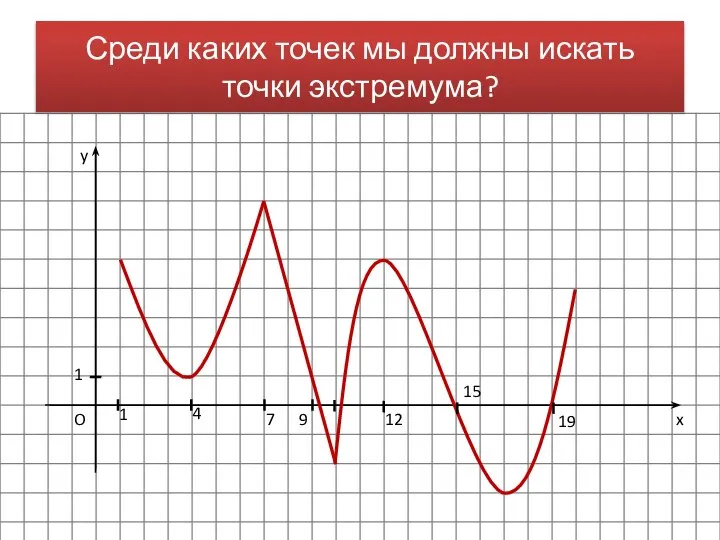
- 15. x y O 1 1 4 7 9 12 15 19 Среди каких точек мы должны
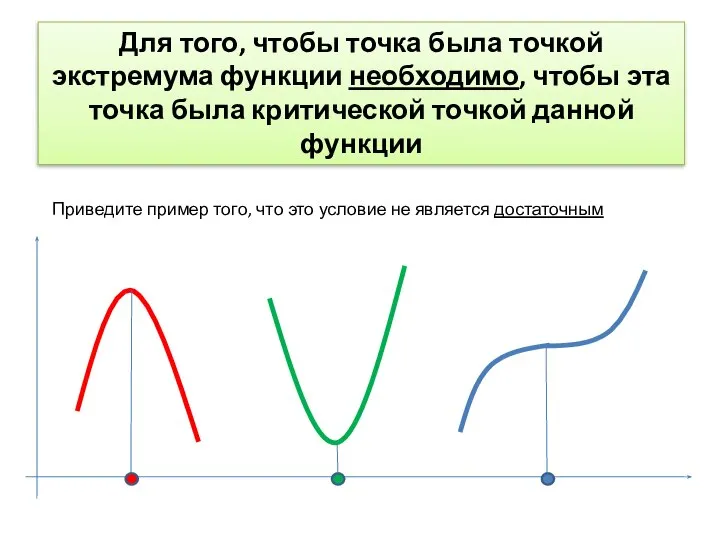
- 16. Для того, чтобы точка была точкой экстремума функции необходимо, чтобы эта точка была критической точкой данной
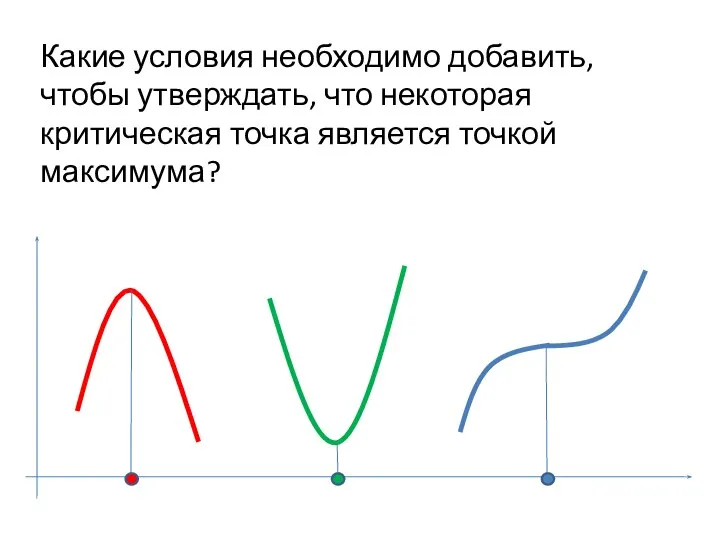
- 17. Какие условия необходимо добавить, чтобы утверждать, что некоторая критическая точка является точкой максимума?
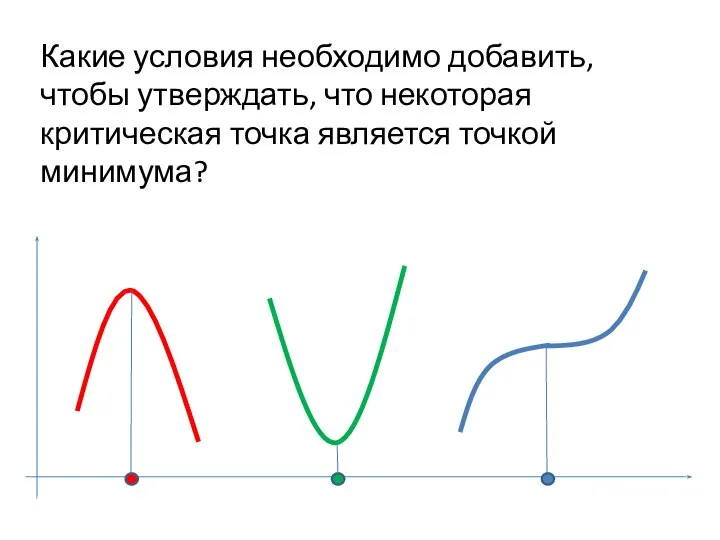
- 18. Какие условия необходимо добавить, чтобы утверждать, что некоторая критическая точка является точкой минимума?
- 20. Скачать презентацию



 Решение задач всех типов на обыкновенные дроби
Решение задач всех типов на обыкновенные дроби Введение в математический анализ
Введение в математический анализ Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  Восход и заход солнца с точки зрения графика тригонометрических функций
Восход и заход солнца с точки зрения графика тригонометрических функций Десятичные дроби. Уравнения
Десятичные дроби. Уравнения Таблица сложения
Таблица сложения Точечное оценивание параметров распределений случайных величин
Точечное оценивание параметров распределений случайных величин Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна
Преподаватель математики и информатики ГБОУ СПО РО «Константиновский педагогический колледж» Алексей Юлия Вадимовна Повторение вычисления двухзначных чисел столбиком с переходом через десяток
Повторение вычисления двухзначных чисел столбиком с переходом через десяток Теорема об интегрировании рядов Фурье
Теорема об интегрировании рядов Фурье Презентация. Ромб. Квадрат
Презентация. Ромб. Квадрат Презентация на тему Декартовы координаты (8 класс)
Презентация на тему Декартовы координаты (8 класс)  Построить линейный угол двугранного угла
Построить линейный угол двугранного угла Золотое сечение
Золотое сечение Генеалогическое древо семьи Бернулли
Генеалогическое древо семьи Бернулли Математикадан 5 класста үткәрелгән Тигезләмә темасын йомгаклау дәресе планы
Математикадан 5 класста үткәрелгән Тигезләмә темасын йомгаклау дәресе планы Сложение и вычитание чисел
Сложение и вычитание чисел Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Метод интервалов. 8 класс
Метод интервалов. 8 класс Случайные величины
Случайные величины Среднее арифметическое. Задания
Среднее арифметическое. Задания Тела вращения. Открытый урок
Тела вращения. Открытый урок Диагонали треугольника равны
Диагонали треугольника равны Презентация на тему Правила вычисления производных
Презентация на тему Правила вычисления производных  Углы. Прямой и развернутый углы
Углы. Прямой и развернутый углы Распознавание и называние геометрических фигур
Распознавание и называние геометрических фигур Функция, ее график и свойства
Функция, ее график и свойства Линейная презентация
Линейная презентация