- Главная
- Математика
- Неравенства. Логарифмические неравенства

Содержание
- 2. Логарифмические неравенства
- 3. 0 4 + + - а Ответ: х∈ (0;1)U(81;+∞) a
- 4. ОДЗ: Показательные неравенства ≤ 1
- 5. 3 9 + + - - -9 Ответ: U (1;∞) а +
- 6. Как решать финансовые задачи ИЛИ «Финансовая математика» Виды задач Банки, вклады, кредиты Оптимальный выбор
- 7. 9/9∙S∙k - x1 = 8/9∙S 8/9∙S∙k - x2 = 7/9∙S 7/9∙S∙k - x3 = 6/9∙S 6/9∙S∙k
- 8. 9/9∙S∙k - x1 = 8/9∙S 8/9∙S∙k - x2 = 7/9∙S 7/9∙S∙k - x3 = 6/9∙S 6/9∙S∙k
- 9. 5∙S∙k - Z = 4∙S 5S∙1,03 - Z = 4∙S 5∙450000∙1,03 - Z = 4∙450000 2250000∙1,03
- 10. 2. а) √10y (кг алюминия) б) √10∙(20-y) (кг никеля) В двух областях есть по 20 рабочих,
- 11. 2. а) √10y (кг алюминия) б) √10∙(20-y) (кг никеля) В двух областях есть по 20 рабочих,
- 12. В двух областях есть по 20 рабочих, каждый из которых готов трудиться по 10 часов в
- 13. 2. а) √10y (кг алюминия) б) √10∙(20-y) (кг никеля) 1. а) x (кг алюминия) б) 20-x
- 15. Скачать презентацию
Слайд 30
4
+
+
-
а
Ответ: х∈ (0;1)U(81;+∞)
a
0
4
+
+
-
а
Ответ: х∈ (0;1)U(81;+∞)
a
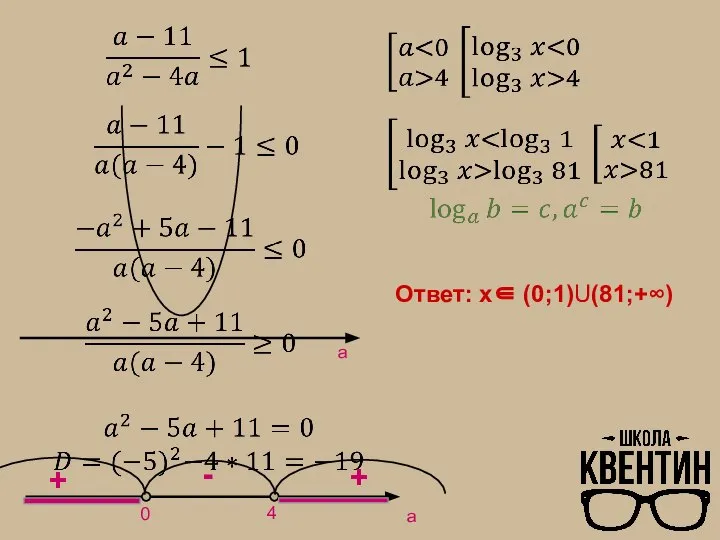
Слайд 4ОДЗ:
Показательные неравенства
≤ 1
ОДЗ:
Показательные неравенства
≤ 1

Слайд 53
9
+
+
-
-
-9
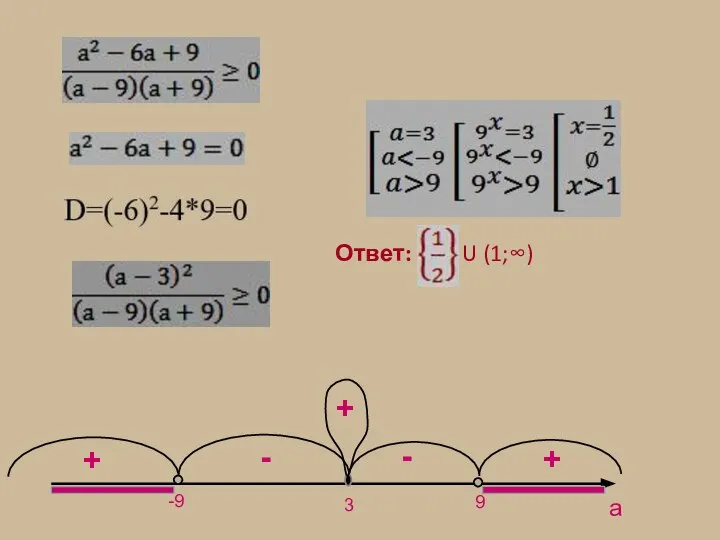
Ответ:
U (1;∞)
а
+
3
9
+
+
-
-
-9
Ответ:
U (1;∞)
а
+
Слайд 6Как решать финансовые задачи
ИЛИ «Финансовая математика»
Виды задач
Банки, вклады, кредиты
Оптимальный выбор
Как решать финансовые задачи
ИЛИ «Финансовая математика»
Виды задач
Банки, вклады, кредиты
Оптимальный выбор

Слайд 79/9∙S∙k - x1 = 8/9∙S
8/9∙S∙k - x2 = 7/9∙S
7/9∙S∙k - x3 =
9/9∙S∙k - x1 = 8/9∙S
8/9∙S∙k - x2 = 7/9∙S
7/9∙S∙k - x3 =

6/9∙S∙k - x4 = 5/9∙S
5/9∙S∙k - 57500 = 4/9∙S
4/9∙S∙k - x6 = 3/9∙S
3/9∙S∙k - x7 = 2/9∙S
2/9∙S∙k - x8 = 1/9∙S
1/9∙S∙k - x9 = 0
S – сумма кредита = ?
r (проценты %) = 3%
k (повышающий коэффициент) = 1,03
(k =1+r/100)
n = 9 месяцев
xn – выплаты
x5 = 57500
x1+ x2+…+ x8+ x9 = (сумма всех выплат) = ?
d (разность прогрессии) = 1/9
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Слайд 89/9∙S∙k - x1 = 8/9∙S
8/9∙S∙k - x2 = 7/9∙S
7/9∙S∙k - x3 =
9/9∙S∙k - x1 = 8/9∙S
8/9∙S∙k - x2 = 7/9∙S
7/9∙S∙k - x3 =

6/9∙S∙k - x4 = 5/9∙S
5/9∙S∙k - 57500 = 4/9∙S
4/9∙S∙k - x6 = 3/9∙S
3/9∙S∙k - x7 = 2/9∙S
2/9∙S∙k - x8 = 1/9∙S
1/9∙S∙k - x9 = 0
5/9S∙1,03 - 57500 = 4/9∙S | ∙9
5S∙1,03 - 517500 = 4∙S
5,15∙S - 4∙S = 517500
1,15∙S = 517500
S = 450000
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
S – сумма кредита
xn – выплаты
k = 1,03
x5 = 57500
Слайд 95∙S∙k - Z = 4∙S
5S∙1,03 - Z = 4∙S
5∙450000∙1,03 - Z =
5∙S∙k - Z = 4∙S
5S∙1,03 - Z = 4∙S
5∙450000∙1,03 - Z =

2250000∙1,03 - Z = 1800000
Z = 2317500 - 1800000
Z = 517000
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
9/9∙S∙k - x1 = 8/9∙S
8/9∙S∙k - x2 = 7/9∙S
7/9∙S∙k - x3 = 6/9∙S
6/9∙S∙k - x4 = 5/9∙S
5/9∙S∙k - x5 = 4/9∙S
4/9∙S∙k - x6 = 3/9∙S
3/9∙S∙k - x7 = 2/9∙S
2/9∙S∙k - x8 = 1/9∙S
1/9∙S∙k - x9 = 0
S = 450000
k = 1,03
x1+ x2+…+ x8+ x9 = Z (сумма выплат)
9/9 + 8/9 + 7/9 +…+ 2/9 + 1/9 = 45/9 = 5
8/9 + 7/9 +…+ 2/9 + 1/9 = 36/9 = 4
Слайд 102. а) √10y (кг алюминия)
б) √10∙(20-y) (кг никеля)
В двух областях есть
2. а) √10y (кг алюминия)
б) √10∙(20-y) (кг никеля)
В двух областях есть

Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 3 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
1. а) x (кг алюминия)
б) 20-x (кг никеля)
y2 → y
y → √y
x(рабочих) ∙ 10ч ∙ 0,1кг/ч = x
Слайд 112. а) √10y (кг алюминия)
б) √10∙(20-y) (кг никеля)
В двух областях есть
2. а) √10y (кг алюминия)
б) √10∙(20-y) (кг никеля)
В двух областях есть

Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 3 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
1. а) x (кг алюминия)
б) 20-x (кг никеля)
Слайд 12В двух областях есть по 20 рабочих, каждый из которых готов трудиться
В двух областях есть по 20 рабочих, каждый из которых готов трудиться

Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 3 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
2. а) √10y (кг алюминия)
б) √10∙(20-y) (кг никеля)
1. а) x (кг алюминия)
б) 20-x (кг никеля)
Слайд 132. а) √10y (кг алюминия)
б) √10∙(20-y) (кг никеля)
1. а) x (кг
2. а) √10y (кг алюминия)
б) √10∙(20-y) (кг никеля)
1. а) x (кг

б) 20-x (кг никеля)
f(y) = 20 + √10y + √10∙(20-y)
+
Найдём точку максимума функции
f '(y) = 0
y = 10

 Решение уравнений
Решение уравнений Решение задач Параллельные прямые
Решение задач Параллельные прямые Виды углов. Равные углы. Измерение углов. Задачи
Виды углов. Равные углы. Измерение углов. Задачи Координатная плоскость
Координатная плоскость Реши задачу
Реши задачу Графическое и табличное представление информации
Графическое и табличное представление информации Виды графов. Тема 4.2
Виды графов. Тема 4.2 Радиус и диаметр окружности
Радиус и диаметр окружности 1ce713f2e27cb837f4d7376560237c07
1ce713f2e27cb837f4d7376560237c07 Математический кроссворд
Математический кроссворд Арифметические действия с десятичными дробями. Математический тренажёр
Арифметические действия с десятичными дробями. Математический тренажёр Поразрядная конъюнкция. Способы решения задания ЕГЭ №15 (№18)
Поразрядная конъюнкция. Способы решения задания ЕГЭ №15 (№18) Определение и знаки тригонометрических функций
Определение и знаки тригонометрических функций Умножение и деление. Урок-путешествие
Умножение и деление. Урок-путешествие Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление Устный счет на уроках математики
Устный счет на уроках математики Длина окружности
Длина окружности Деление с остатком. Теоретическая часть
Деление с остатком. Теоретическая часть Векторы. Линейные операции над векторами. Разложение вектора по базису
Векторы. Линейные операции над векторами. Разложение вектора по базису Устный счет
Устный счет Решение квадратных уравнений с параметрами. Метод плавающей параболы
Решение квадратных уравнений с параметрами. Метод плавающей параболы Представление о ломаной линии и многоугольнике
Представление о ломаной линии и многоугольнике Умножение вектора на число
Умножение вектора на число Задачи на сравнение
Задачи на сравнение Glava_5_-_Proektirovanie_vyborki_Gubko_A_M
Glava_5_-_Proektirovanie_vyborki_Gubko_A_M Теория вероятностей. Равновероятные возможности
Теория вероятностей. Равновероятные возможности Конус - тело вращения
Конус - тело вращения Управление мыслительной деятельностью при решении математических заданий
Управление мыслительной деятельностью при решении математических заданий