Содержание
- 2. Лекция № 3 Множественная регрессия и корреляция
- 3. Уравнение множественной регрессии Основная цель множественной регрессии– построить модель с большим числом факторов, определив при этом
- 4. Отбор факторов при построении уравнения множественной регрессии Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
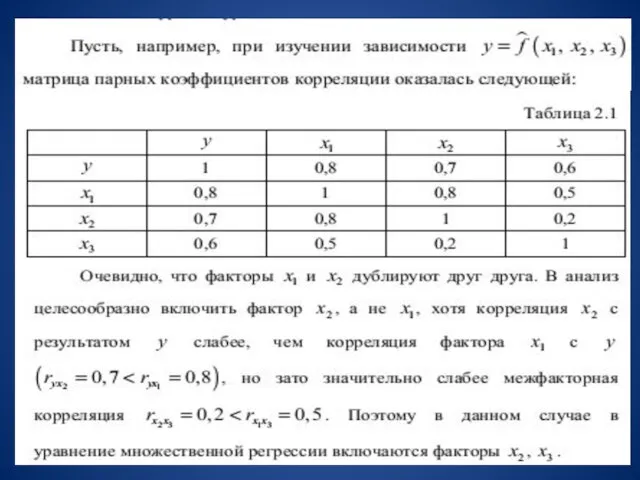
- 6. Отбор факторов обычно осуществляется в две стадии: подбираются факторы исходя из сущности проблемы; на основе матрицы
- 8. Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий: Затрудняется интерпретация параметров множественной регрессии как
- 10. Существует ряд подходов преодоления сильной межфакторной корреляции: самый простой путь устранения мультиколлинеарности состоит в исключении из
- 11. Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии: Метод исключения– отсев факторов из полного
- 12. Метод наименьших квадратов(МНК). Свойства оценок на основе МНК
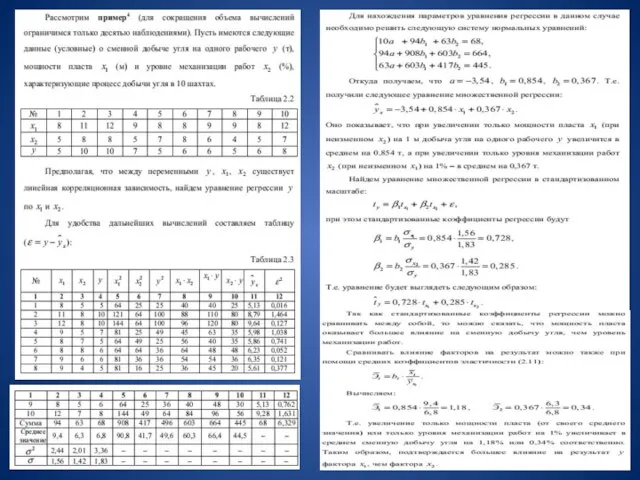
- 16. Проверка существенности факторов и показатели качества регрессии Практическая значимость уравнения множественной регрессии оценивается с помощью показателя
- 17. Сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того
- 23. Скачать презентацию


















 Нулевой угловой коэффицент
Нулевой угловой коэффицент В стране математики
В стране математики Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Площади. Формула Пика
Площади. Формула Пика Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Первые уроки в 5 кассе
Первые уроки в 5 кассе Решение задач с помощью рациональных уравнений. 8 класс
Решение задач с помощью рациональных уравнений. 8 класс Таблица сложения
Таблица сложения Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Элементы теории вероятности
Элементы теории вероятности График функции. Урок применения знаний и умений. Класс: 8
График функции. Урок применения знаний и умений. Класс: 8 Иррациональные уравнения
Иррациональные уравнения Смежные углы
Смежные углы Определение арифметического корня п-ой степени
Определение арифметического корня п-ой степени Основные понятия комбинаторики
Основные понятия комбинаторики Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс) 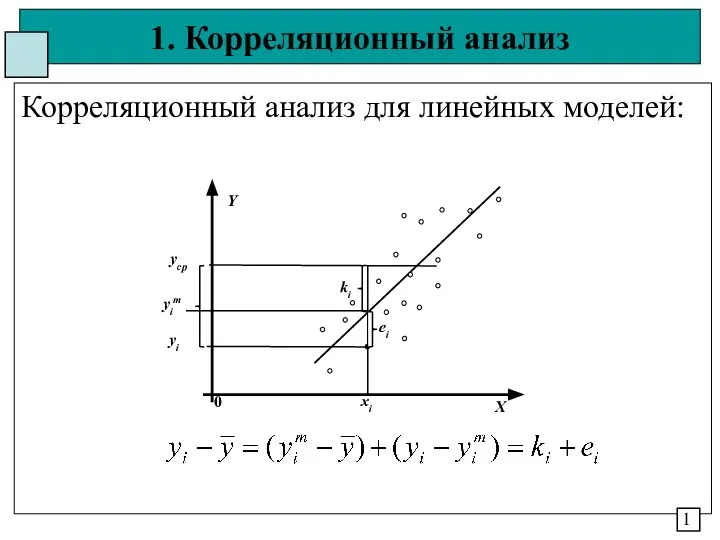 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Решение тригонометрических уравнений
Решение тригонометрических уравнений Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Спиннеры и метематика
Спиннеры и метематика krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Обратные матрицы
Обратные матрицы Сравнение моделей
Сравнение моделей Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Презентация на тему Многоугольники (1 класс)
Презентация на тему Многоугольники (1 класс)  Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве