Площадь криволинейной трапеции и интеграл

Площадь криволинейной трапеции и интеграл.
у
х

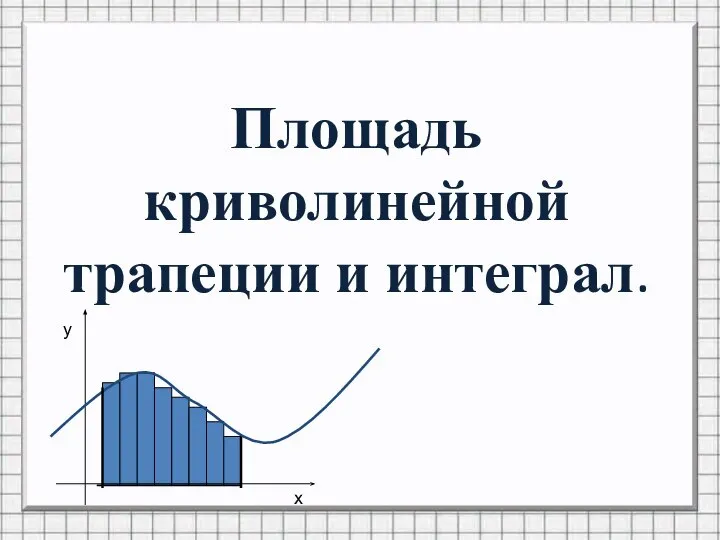
Криволинейная трапеция
Отрезок [a;b] называют основанием
этой криволинейной трапеции
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].

Криволинейная трапеция
0
2
0
0
0
1
-1
-1
2
-1
-2
У=х²+2х
У=0,5х+1

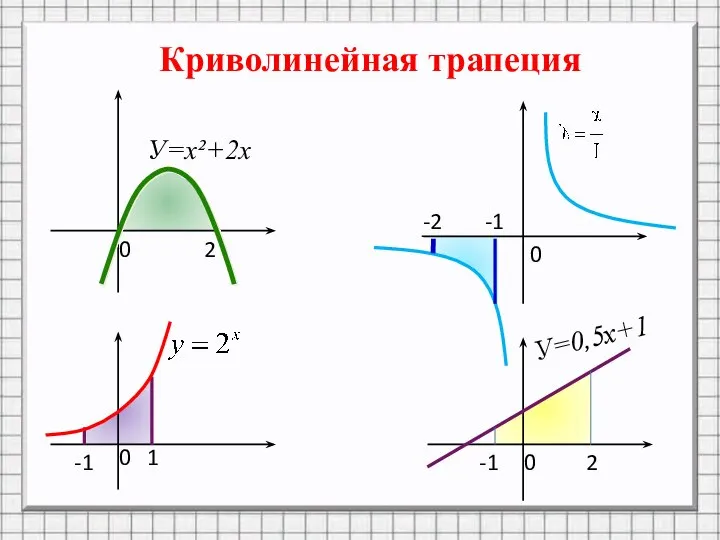
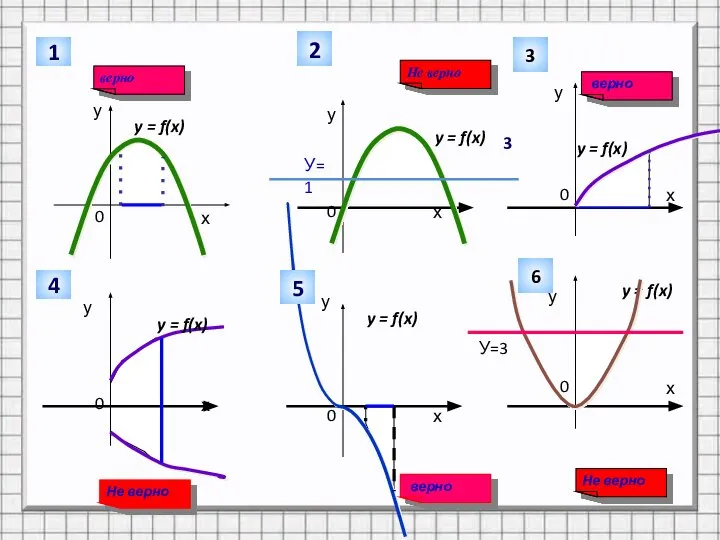
Какие из заштрихованных на рисунке (слайд 5) фигур являются криволинейными трапециями, а какие нет?
Заполнить таблицу

у
1
Не верно
у
у
у
у
у
У=1
2
верно
3
3
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
У=3
4
5
6
Не верно
Не верно
верно
верно

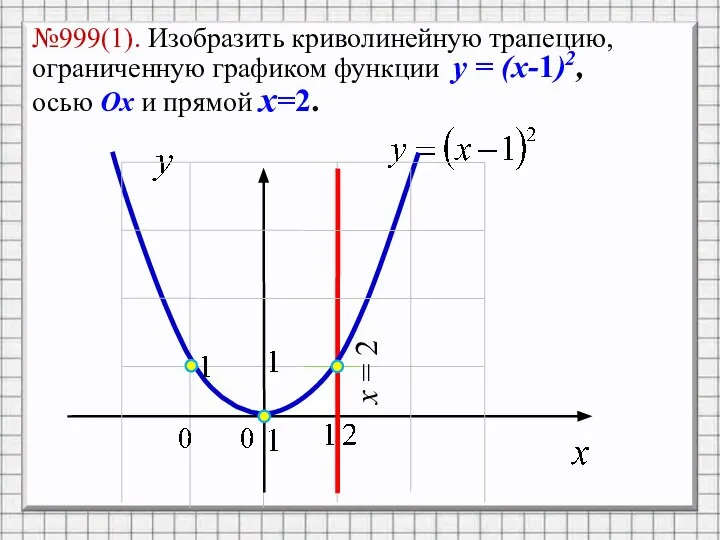
№999(1). Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x=2.
x = 2

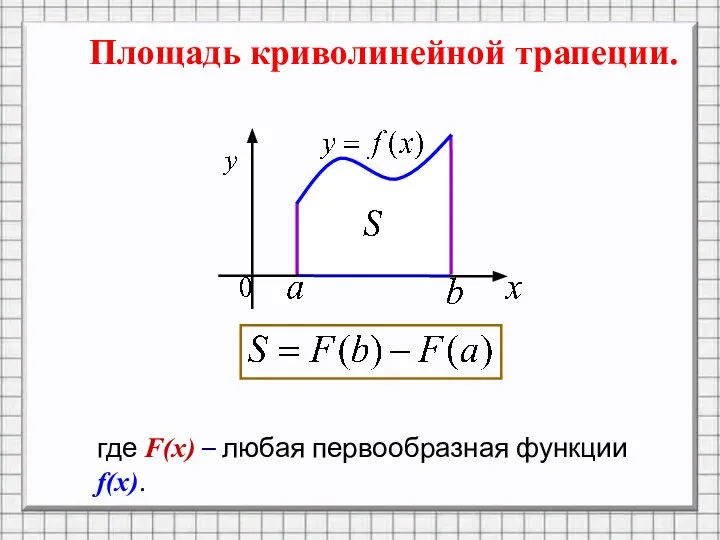
Площадь криволинейной трапеции.
где F(x) – любая первообразная функции f(x).

Формула Ньютона-Лейбница
1643—1727
1646—1716

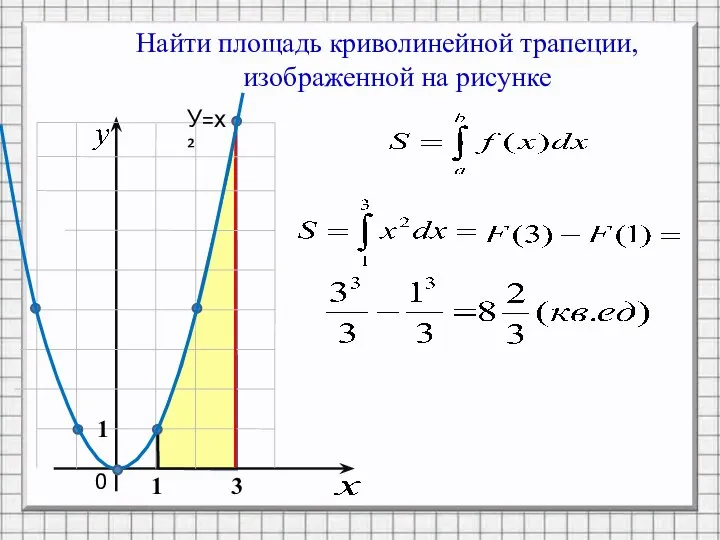
Найти площадь криволинейной трапеции,
изображенной на рисунке
0
1
3
У=х²
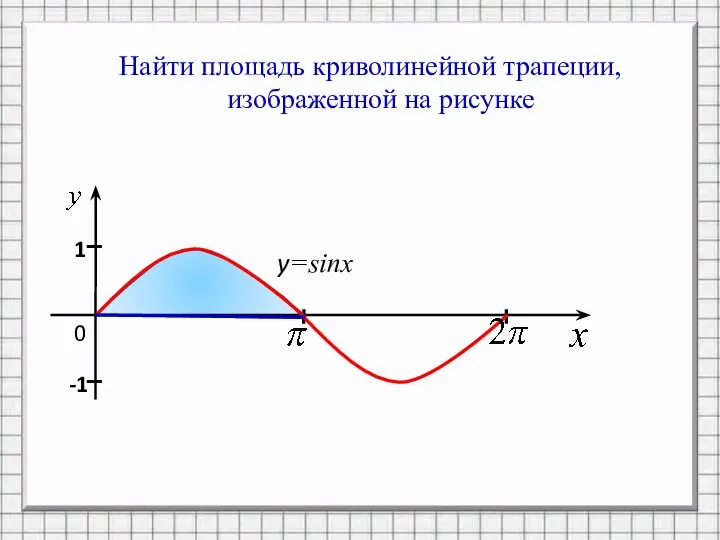
1

Найти площадь криволинейной трапеции,
изображенной на рисунке
0
y=sinx
I
I
1
-1