Содержание
- 2. История. Объём - одна из основных величин, связанных с геометрическими телами. В простейших случаях измеряется числом
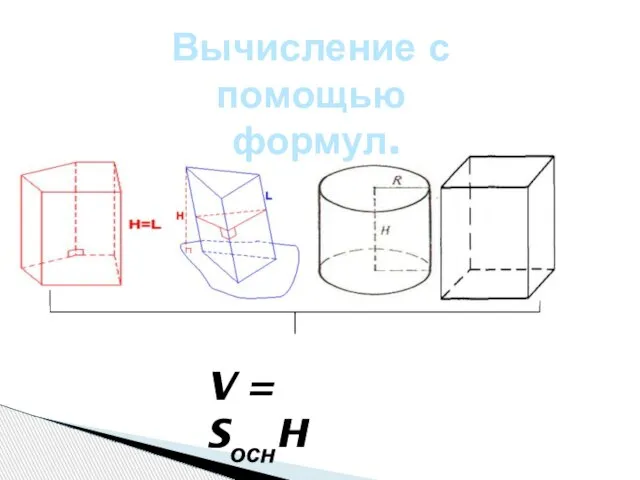
- 3. V = SоснH Вычисление с помощью формул.
- 4. Происходит очень просто. Измеряем размеры и подставляем в формулу! Вывод формул есть в учебнике.
- 5. Закон Архимеда
- 6. Можно вспомнить Закон Архимеда и о том, что 1 литр воды занимает объём в 10 куб.дм.
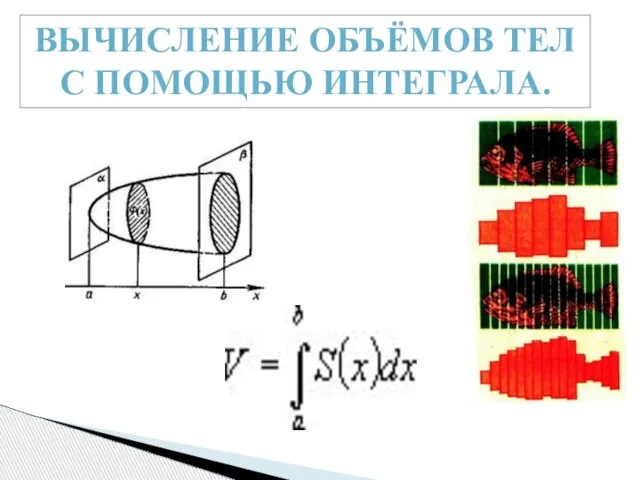
- 7. ВЫЧИСЛЕНИЕ ОБЪЁМОВ ТЕЛ С ПОМОЩЬЮ ИНТЕГРАЛА.
- 8. Принцип Кавальери состоит в том, что если пересечь фигуру семейством всех прямых, параллельных заданной, то длины
- 9. Видный советский ученый, историк математики, профессор Д. Д. Мордухай-Болтовский (1876—1952), которому принадлежит самый совершенный русский перевод
- 11. Скачать презентацию





 Наибольшие и найменьшее значение функции
Наибольшие и найменьшее значение функции Кубический корень
Кубический корень Основные характеристики средств измерений. Лекция 4
Основные характеристики средств измерений. Лекция 4 Логарифмическая функция. Тест
Логарифмическая функция. Тест Уравнение плоскости
Уравнение плоскости Цели урока:
Цели урока: Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Простейшие уравнения
Простейшие уравнения Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Геологические приложения одномерной статистической модели
Геологические приложения одномерной статистической модели Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся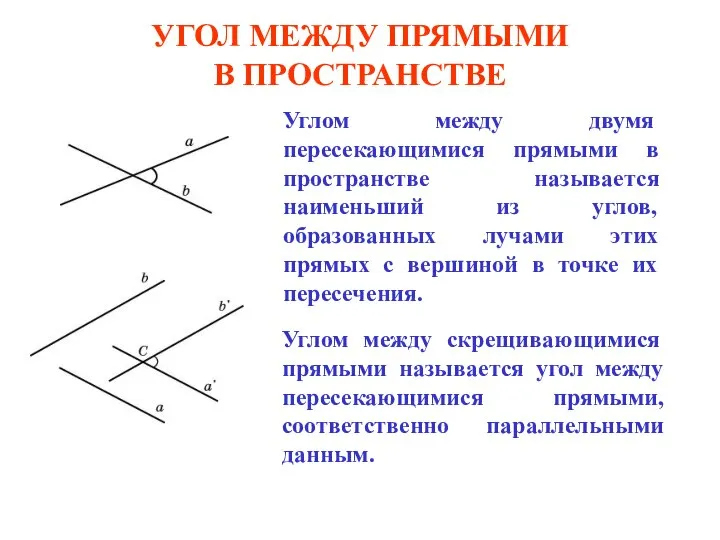 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс
Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс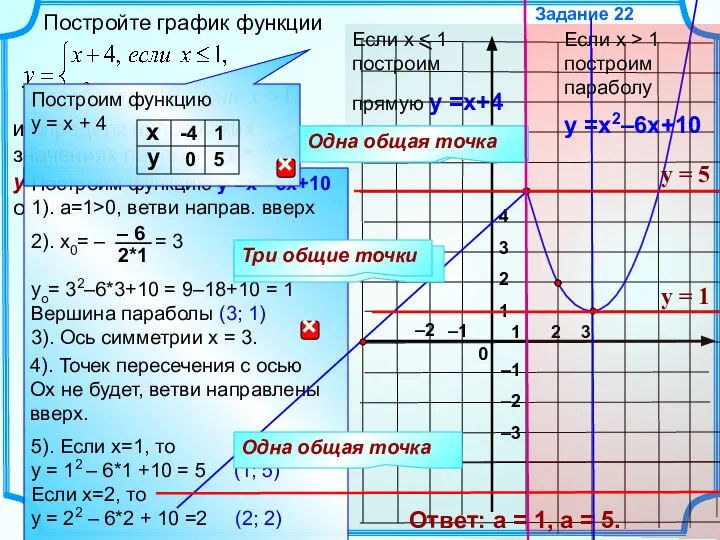 Парабола прямая. Часть II
Парабола прямая. Часть II Второй признак подобия треугольников
Второй признак подобия треугольников Степень с натуральным показателем. Обобщающий урок в 7 классе
Степень с натуральным показателем. Обобщающий урок в 7 классе Решение задач
Решение задач Пирамида
Пирамида Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс)  Упрощение выражений. Тест
Упрощение выражений. Тест Сумма углов треугольника
Сумма углов треугольника Вычисление производной и правила дифференцирования
Вычисление производной и правила дифференцирования Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Математическая тревожность
Математическая тревожность Решение логарифмических уравнений
Решение логарифмических уравнений Решение систем неравенств
Решение систем неравенств Семь чудес Кузбасса 5 класс
Семь чудес Кузбасса 5 класс Признаки равенства треугольников
Признаки равенства треугольников