Слайд 2Задание на два занятия
1.Записать определение 1, слайд №5
Записать к нему пример,

слайд №7
2.Записать определение 2, слайд №8
Записать к нему пример, слайд №9
3.Слайд №15,решить 1,2,3
На следующем занятии решить 4-10
Слайд 3 Вопросы для повторения
1. Какую функцию называют возрастающей?
2. Приведите пример возрастающей функции
3.

Какую функцию называют убывающей?
4. Приведите пример убывающей функции
Слайд 4При исследовании поведения функции вблизи некоторой точки удобно пользоваться понятием окрестности
Окрестностью

точки называется любой интервал, содержащий эту точку. Например,
(2; 6) одна из окрестностей точки 3,
(-3,3; - 2,7) одна из окрестностей точки -3
Слайд 5Определение 1.
Точка х0 называется точкой минимума функции f , если для всех

х из некоторой окрестности точки хо выполнено неравенство
f (хо) ≤ f (х)
Слайд 7Пример 1.
Точка хо=0 является точкой минимума функции f(х) = х2.
Доказательство:
Возьмём х1

= 1 и х2 = 2
Найдём: f(х0) = f(0) = 02 = 0
Найдём: f(х1) = f(1) =12 = 1
Найдём: f(х2) = f(2) = 22 = 4
Видим, что f(х1)≥ f(х0)
f(х2)≥ f(х0)
По определению 1 хо=0 является точкой минимума функции f(х) = х2
Слайд 8Определение 2.
Точка х0 называется точкой максимума функции f , если для всех

х из некоторой окрестности точки хо выполнено неравенство
f (хо) ≥ f(х)
Слайд 9Пример 2.
Точка хо=0 является точкой максимума функции f(х) = -х2.
Доказательство:
Возьмём х1

= 1 и х2 = 2
Найдём: f(х0) = f(0) = 02 = 0
Найдём: f(х1) = f(1) =-12 =- 1
Найдём: f(х2) = f(2) = -22 =- 4
Видим, что f(х1) ≤ f(х0)
f(х2) ≤ f(х0)
По определению 2 хо=0 является точкой максимума функции f(х) =- х2
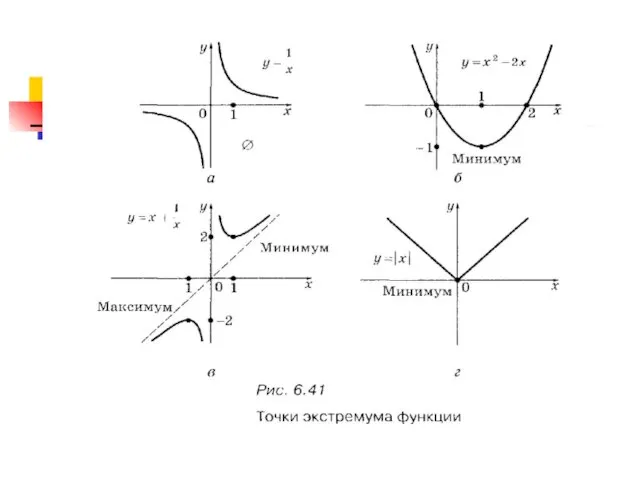
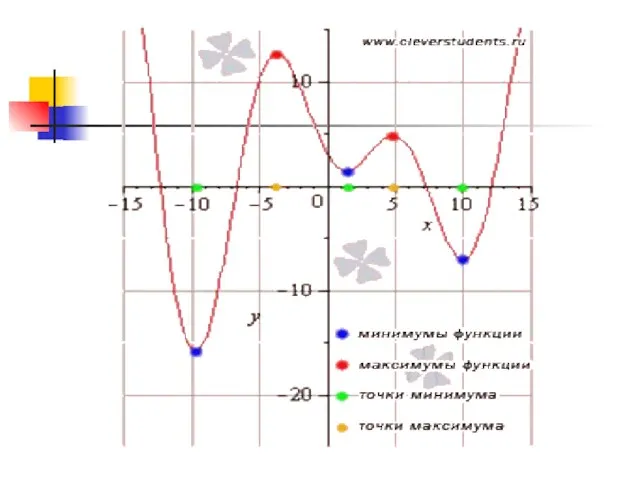
Слайд 12Для точек минимума и максимума функции принято общее название - их называют

точками экстремума.
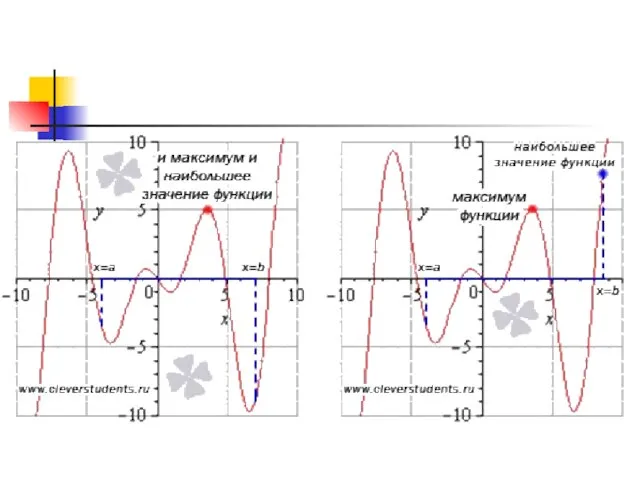
Слайд 14Выполнить задание.
Для функций, изображённых на графиках найти точки минимума и максимума
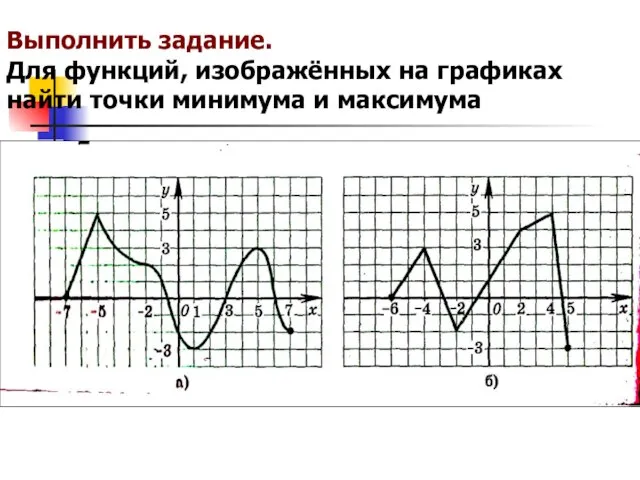
Слайд 15Выполнить задание.
Исследовать на экстремумы:
1.хо = -2, для f(х) = х2 +

4х+3;
2. хо = -2, для f(х) = -х2 - 4х;
3. хо = 1, для f(х) = 2х2 – 4х+3;
4. хо = 3, для f(х) = х2 – 6х+3;
5. хо =-2, для f(х) = -2х2 – 8х.
Слайд 16Выполнить задание.
Исследовать на экстремумы:
6.хо = -1, для f(х) = х2 +

2х+5;
7. хо = -3, для f(х) = -х2 - 6х+1;
8. хо = -1, для f(х) = 2х2 + 4х+3;
9. хо = 3, для f(х) = х2 – 6х+3;
10. хо =-2, для f(х) = -2х2 – 8х+3.
Слайд 17 Вопросы для закрепления
1. Что называют точкой минимума функции? 2. Что называют

точкой максимума функции?
3. Приведите примеры точек максимума и минимума функций.
4. Как принято называть точки минимума и максимума функции?












 Процент
Процент Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Цилиндр. Задачи
Цилиндр. Задачи Деление многочленов
Деление многочленов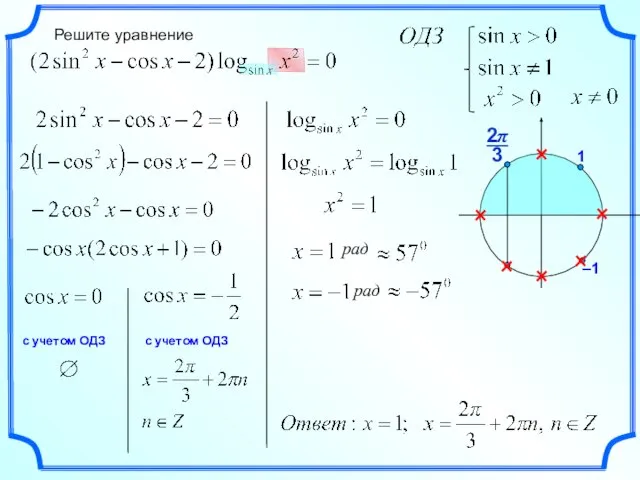 Решение уравнения
Решение уравнения Десятичные дроби. 5 класс
Десятичные дроби. 5 класс Исследование функций и построение графиков
Исследование функций и построение графиков Квадрат. Свойства и признаки квадрата
Квадрат. Свойства и признаки квадрата Треугольник и его виды
Треугольник и его виды Создание системы внеклассной работы в физико-математическом образовании
Создание системы внеклассной работы в физико-математическом образовании Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница
Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница Решение задач. Периметр и площадь
Решение задач. Периметр и площадь Морской бой
Морской бой Презентация на тему Решение задач на пропорциональное деление (4 класс)
Презентация на тему Решение задач на пропорциональное деление (4 класс)  Задачи предельного типа
Задачи предельного типа Уравнения математической физики
Уравнения математической физики Метод следов. Построение следа секущей плоскости
Метод следов. Построение следа секущей плоскости Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс)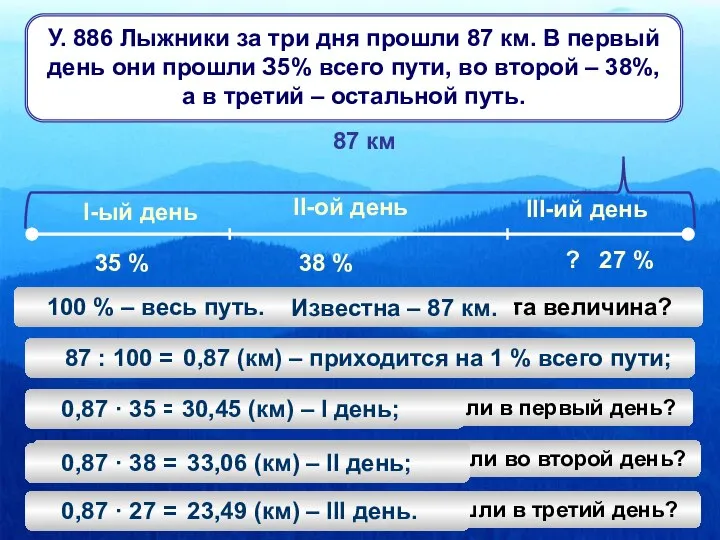 Задачи о лыжниках
Задачи о лыжниках Ромашка
Ромашка Графики уравнений. Преобразование графиков уравнений, содержащих модуль
Графики уравнений. Преобразование графиков уравнений, содержащих модуль Узагальнення і систематизація матеріалу по дробам
Узагальнення і систематизація матеріалу по дробам Объем пирамиды
Объем пирамиды Волшебное число ПИ
Волшебное число ПИ Precvičujeme. Správne riešenia
Precvičujeme. Správne riešenia Точки экстремума
Точки экстремума Системы уравнений
Системы уравнений Сравнительный анализ методов полиэдральной аппроксимации при построении гарантирующего решения
Сравнительный анализ методов полиэдральной аппроксимации при построении гарантирующего решения