Слайд 2ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Теория вероятностей – это раздел математики изучающий закономерности массовых случайных

событий.
Изучение каждого явления в порядке наблюдения или производства опыта связанно с осуществлением некоторого комплекса условий (испытаний). Всякий результат или исход испытания называется событием.
Опр. Если событие при заданных условиях может произойти или не произойти, то оно называется случайным.
Слайд 3Опр. В том случае, когда событие непременно должно произойти, то оно называется

достоверным, а в том случае, когда оно заведомо не может произойти – невозможным.
Опр. События называются несовместными, если каждый раз возможно появление только одного из них.
Слайд 4Опр. События называются совместными, если в данных условиях появление одного из этих

событий не исключает появления другого при том же испытании.
Опр. События называются противоположными, если в условиях испытания они, являясь единственным его исходами, несовместны.
Вероятность события рассматривается как мера объективной возможности появления случайного события.
Слайд 5КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Слайд 10Опр. События А, В, С – называются независимыми в совокупности, если вероятность

каждого из них не меряется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации.
Слайд 17ПОВТОРЕНИЕ ИСПЫТАНИЙ. ФОРМУЛА БЕРНУЛЛИ
Опр. Если производятся испытания, при которых вероятность появления события

А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно испытания А.
















 Нулевой угловой коэффицент
Нулевой угловой коэффицент В стране математики
В стране математики Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Площади. Формула Пика
Площади. Формула Пика Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Первые уроки в 5 кассе
Первые уроки в 5 кассе Решение задач с помощью рациональных уравнений. 8 класс
Решение задач с помощью рациональных уравнений. 8 класс Таблица сложения
Таблица сложения Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Элементы теории вероятности
Элементы теории вероятности График функции. Урок применения знаний и умений. Класс: 8
График функции. Урок применения знаний и умений. Класс: 8 Иррациональные уравнения
Иррациональные уравнения Смежные углы
Смежные углы Определение арифметического корня п-ой степени
Определение арифметического корня п-ой степени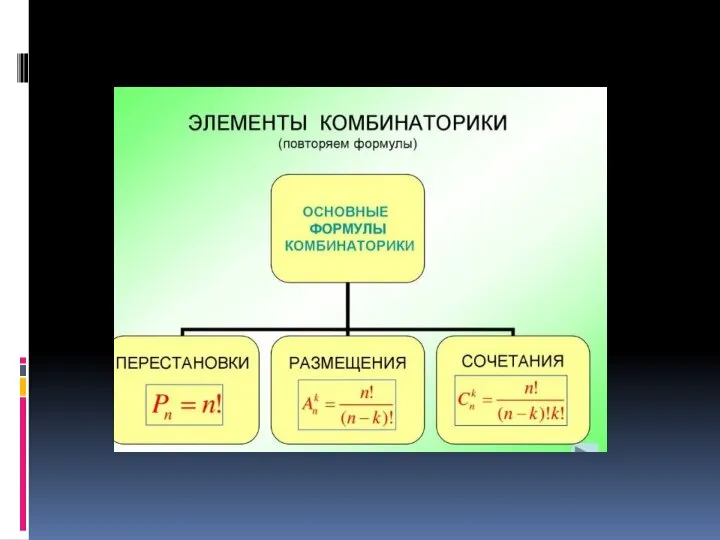 Основные понятия комбинаторики
Основные понятия комбинаторики Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс) 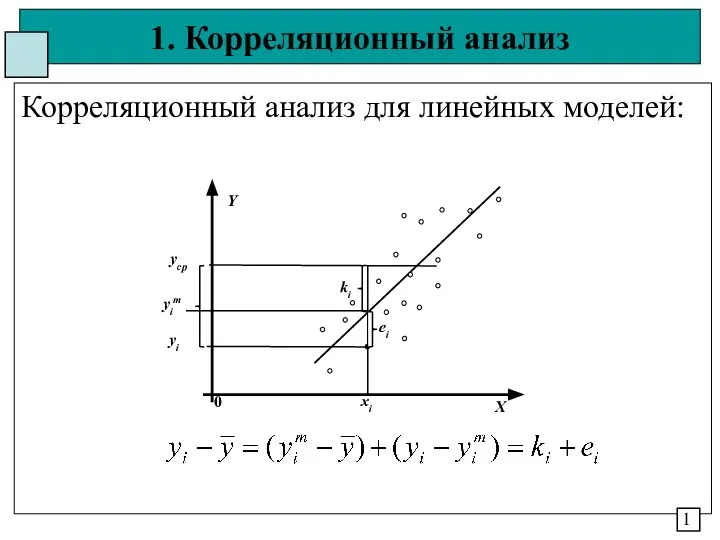 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Решение тригонометрических уравнений
Решение тригонометрических уравнений Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Спиннеры и метематика
Спиннеры и метематика krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Обратные матрицы
Обратные матрицы Сравнение моделей
Сравнение моделей Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Презентация на тему Многоугольники (1 класс)
Презентация на тему Многоугольники (1 класс)  Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве