Содержание
- 2. Обозначается: D 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Определитель – это число, которое вычисляется по формулам, схемам и правилам.
- 3. Определителем первого порядка матрицы называется число То есть: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 4. Определителем второго порядка называется число, которое определяется по правилу: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 5. Определителем третьего порядка называется число, которое определяется по правилу: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
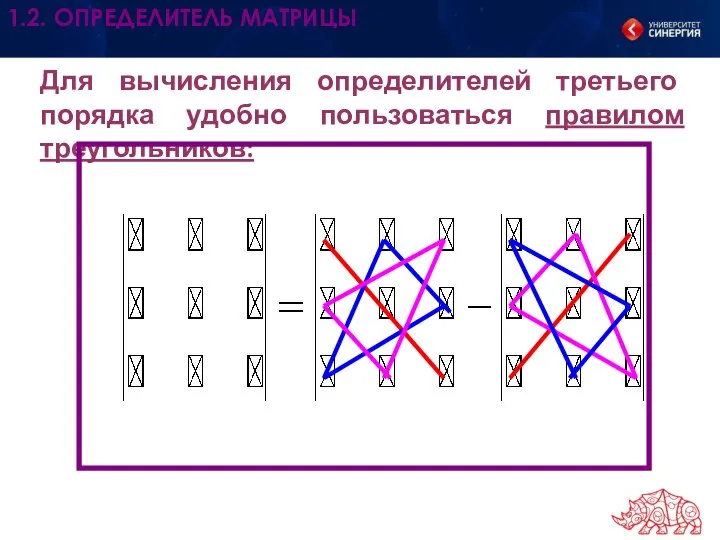
- 6. Для вычисления определителей третьего порядка удобно пользоваться правилом треугольников: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 7. Пример. Вычислить определители матриц: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 8. Решение: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 9. Минором элемента определителя D называется такой новый определитель, полученный из данного определителя вычеркиванием строки и столбца,
- 10. Алгебраическим дополнением элемента аij определителя D называется минор Mij этого элемента, умноженный на (-1)s , где
- 11. В частности, минор элемента определителя третьего порядка найдется по правилу: Его алгебраическое дополнение: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 12. Свойства определителей 1 Определитель транспонированной матрицы равен определителю исходной матрицы. 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
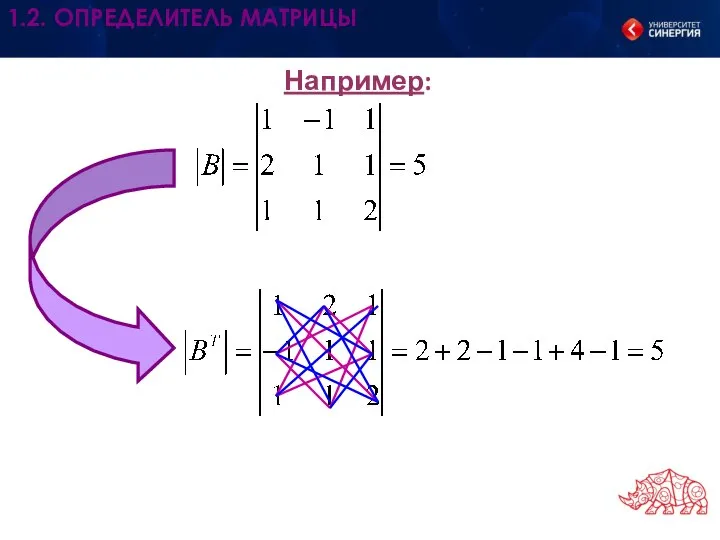
- 13. Например: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 14. 2 При перестановке двух строк или столбцов определитель изменит свой знак на противоположный. 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 15. Например: Меняем местами первую и вторую строки: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 16. 3 Если определитель имеет две одинаковые строки или столбца, то он равен нулю. 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 17. Например: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 18. 4 Общий множитель строки или столбца можно выносить за знак определителя. 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 19. Например: Выносим из второй строки множитель 2: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 20. 5 Определитель не изменится, если к элементам одной строки или столбца прибавить соответственные элементы другой строки
- 21. Например: Первую строку умножаем на 2 и складываем со второй: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 22. 6 Треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали- нули, равен произведению
- 23. Например: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ = 3·3·3=27
- 24. 7 Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения: 1.2. ОПРЕДЕЛИТЕЛЬ
- 25. Пример. Вычислить определитель: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 26. Раскладываем определитель по третьей строке: Решение: = Находим алгебраические дополнения: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 27. Подставляем полученный результат: = 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 28. Вывод: Способы вычисления определителя. 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 29. 1 Определители второго и третьего порядка вычисляют по схемам. 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 30. 2 Определитель можно вычислить с помощью его разложения по элементам строки или столбца (свойство 7). 1.2.
- 31. 3 Определитель можно вычислить способом приведения его к треугольному виду. 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 32. Этот способ основан на том, что по свойству 6, треугольный определитель равен произведению элементов главной диагонали.
- 33. Чтобы получить треугольный определитель, надо, по свойству 5 к какой-либо строке или столбцу определителя 1.2. ОПРЕДЕЛИТЕЛЬ
- 34. прибавить соответствующие элементы другой строки или столбца, умноженные на одно и тоже число, до тех пор,
- 35. Вычислить определитель: 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 36. Практикум 2.1 Определители 1.2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
- 38. Скачать презентацию

































 8 класс
8 класс Конструирование пирамиды. Пирамиды в архитектуре и в повседневной жизни
Конструирование пирамиды. Пирамиды в архитектуре и в повседневной жизни Адмирал Морского Флота Федор Федорович Ушаков
Адмирал Морского Флота Федор Федорович Ушаков Графіка. Лінійна перспектива. Графічне зображення ,,Куб
Графіка. Лінійна перспектива. Графічне зображення ,,Куб Тетраэдр и параллелепипед. Геометрия 10 класс
Тетраэдр и параллелепипед. Геометрия 10 класс Сумма углов треугольника
Сумма углов треугольника Интегральное исчисление
Интегральное исчисление Презентация на тему Правильные многоугольники (9 класс)
Презентация на тему Правильные многоугольники (9 класс)  Подготовка к контрольной работе
Подготовка к контрольной работе Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Умножение дробей
Умножение дробей Конкурсное задание УРОК
Конкурсное задание УРОК Эконометрика. Семинар 2. Решение задачи 4
Эконометрика. Семинар 2. Решение задачи 4 Площадь квадрата, прямоугольника, параллелограмма
Площадь квадрата, прямоугольника, параллелограмма Прибавление суммы к числу
Прибавление суммы к числу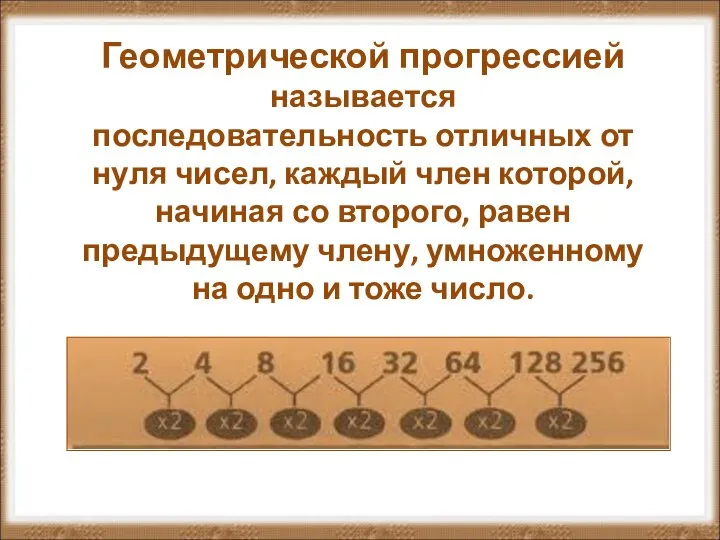 Возможности геометрической прогрессии в отношении растения одуванчик (часть 2)
Возможности геометрической прогрессии в отношении растения одуванчик (часть 2) izmerenie_otrezkov_7_klass
izmerenie_otrezkov_7_klass Связь между суммой и слагаемыми
Связь между суммой и слагаемыми Презентация на тему Умножение десятичных дробей на натуральные числа
Презентация на тему Умножение десятичных дробей на натуральные числа  Презентация на тему СИНУСОИДЫ, КОСИНУСОИДЫ
Презентация на тему СИНУСОИДЫ, КОСИНУСОИДЫ  Высказывание. Логические операции
Высказывание. Логические операции Письмове додавання і віднімання, коли сума розрядних одиниць дорівнює 10
Письмове додавання і віднімання, коли сума розрядних одиниць дорівнює 10 Отношение чисел
Отношение чисел Теория вероятностей
Теория вероятностей Системы массового обслуживания
Системы массового обслуживания Высшая математика. Экзамен (1й курс)
Высшая математика. Экзамен (1й курс) Учимся писать цифры с Дракошей
Учимся писать цифры с Дракошей Решение практических задач с применением среднего арифметического. 5 класс
Решение практических задач с применением среднего арифметического. 5 класс