Фигуры вращения

ПОНЯТИЕ ФИГУРЫ ВРАЩЕНИЯ
Фигуры вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.

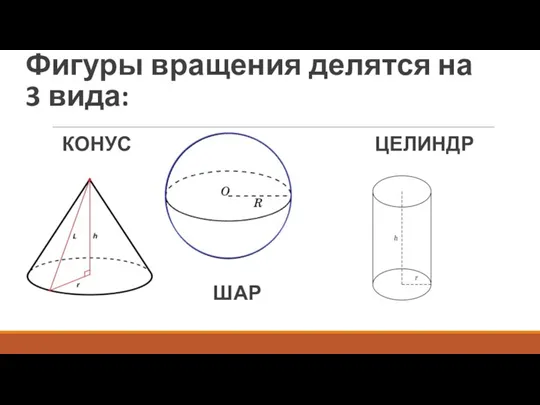
Фигуры вращения делятся на 3 вида:
КОНУС ЦЕЛИНДР
ШАР

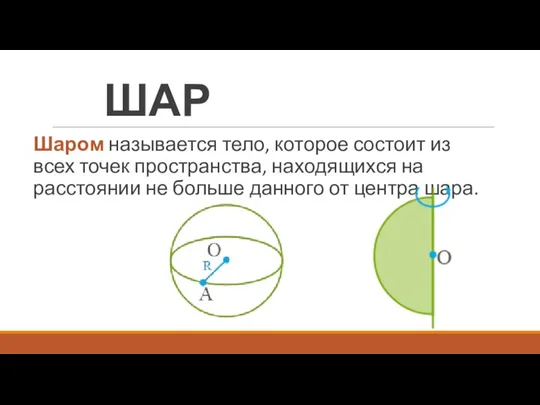
ШАР
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии не больше данного от центра шара.

Основные формулы
Площадь поверхности шара вычисляется по формулам:
Если нам известен радиус:
Если нам известен диаметр:
Объем шара измеряется по формуле:
:

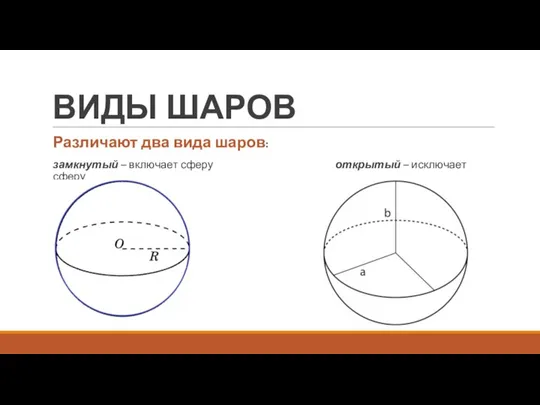
ВИДЫ ШАРОВ
Различают два вида шаров:
замкнутый – включает сферу открытый – исключает сферу

Свойства шара
Свойство 1. Любое сечение шара плоскостью является кругом.
Свойство 2. Любое сечение сферы плоскостью является окружностью.
Свойство 3. Все точки сферы равноудалены от ее центра.
Свойство 4. Сфера имеет самый большой объем среди всех фигур в пространстве, имеющих одинаковую площадь поверхности.
Свойство 5 Через две любые диаметрально противоположные точки (максимально отдаленные друг от друга точки на окружности) можно провести неограниченное количество кругов для шара или окружностей для сфер радиусом, равным радиусу шара

Части шара
Сегмент шара – это часть шара, отсекаемая плоскостью. Иногда называется шаровым сегментом.

Части шара
Срез шара – часть шара между двумя параллельными плоскостями, пересекающими его. Также может называться шаровым слоем.

Части шара
Сектор шара – состоит из шарового сегмента и конуса, вершина которого находится центре шара, а основание совпадает с основанием сегмента.

Конус
Конус — это тело вращения, которое получается
в результате вращения
прямоугольного треугольника
вокруг его катета.

Виды конуса
1.Косой (наклонный) конус - это конус у которого ось не перпендикулярна основе.

Виды конуса
2. Прямой конус – это конус, в котором прямая соединяет вершину конуса и центр основания, перпендикулярна плоскости основания.

Виды конуса
Усечённый конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

Свойство конуса
Свойство 1.Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
где S — площадь основания
Свойство 2.Площадь боковой поверхности прямого кругового конуса равна
а в общем случае где R — радиус основания, -
— длина образующей, — длина границы основания.

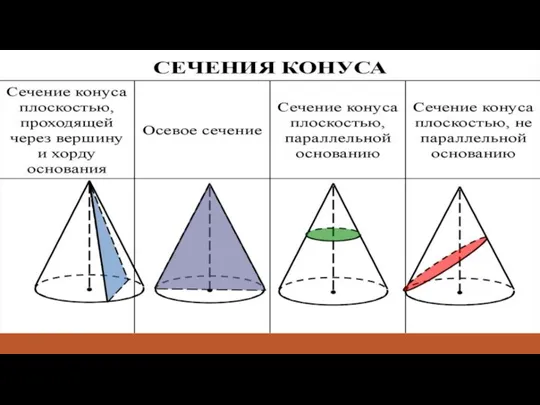
Сечения конуса

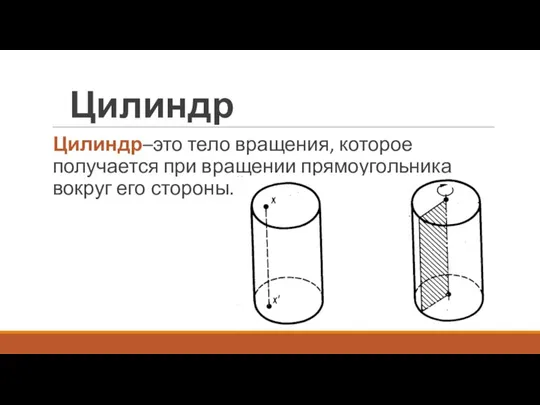
Цилиндр
Цилиндр–это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.

Основные формулы
1.Для прямого кругового цилиндра:
, здесь R — радиус основания цилиндра.
2.Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:
Для кругового цилиндра:

Виды цилиндра
Прямым круговым цилиндром называется цилиндр, у которого в основании лежат равные круги, а образующая перпендикулярна основаниям

Виды цилиндра
Наклонный цилиндр – это цилиндр, образующие которого не перпендикулярны плоскостям его основания.

Основные свойства
Свойство 1. Основания цилиндра равны и параллельны.
Свойство 2. Основания равны и параллельны.
Свойство3.Все образующие цилиндра параллельны и равны друг другу Сечения цилиндра.