Содержание
- 2. Раскраска графов Определение. Пусть G=(V, E) – неориентированный граф и k – натуральное число. Функция f:
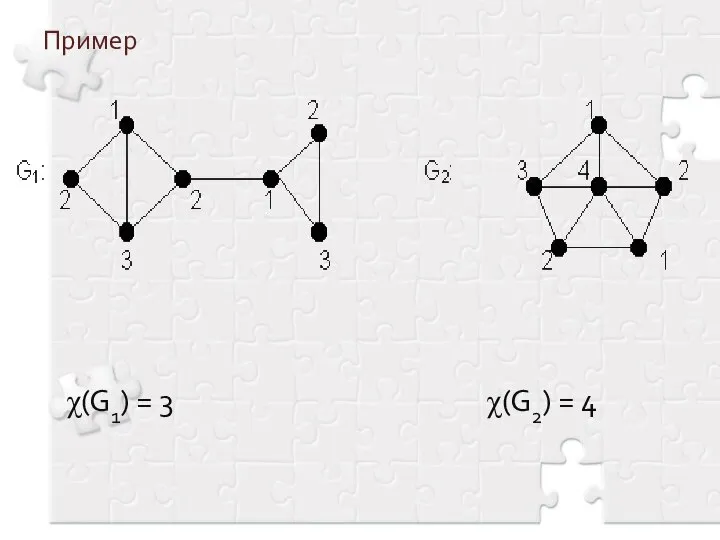
- 3. Пример χ(G1) = 3 χ(G2) = 4
- 4. Задача составления расписаний Предположим, что в учебном центре надо провести несколько занятий за кратчайшее время. Длительность
- 5. Задача распределения ресурсов Необходимо выполнить некоторое множество V={v1,v2,…,vn} работ. Имеется множество S={s1,s2,…,sr} ресурсов, требуемых для выполнения
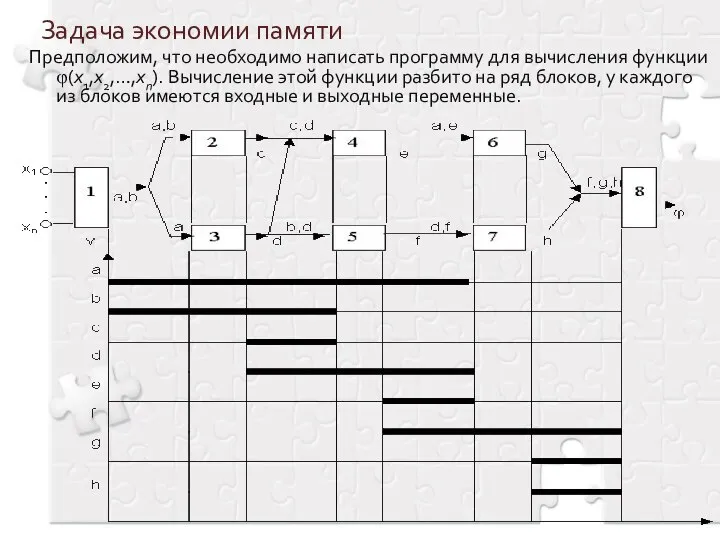
- 6. Задача экономии памяти Предположим, что необходимо написать программу для вычисления функции φ(х1,x2,…,xn). Вычисление этой функции разбито
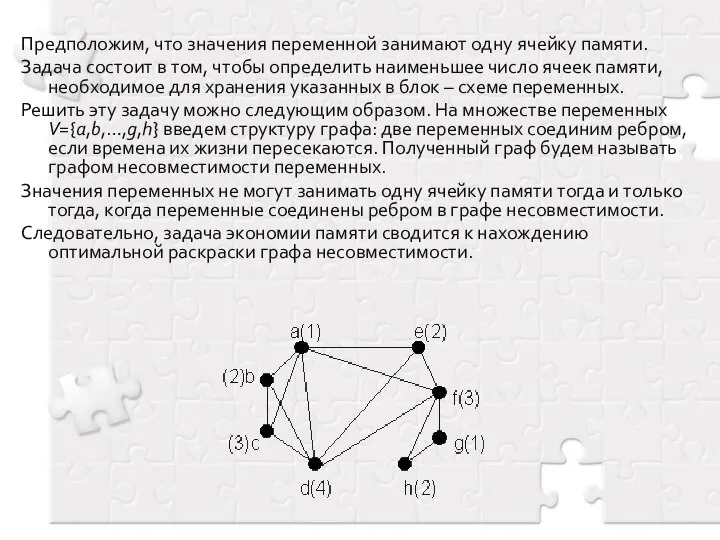
- 7. Предположим, что значения переменной занимают одну ячейку памяти. Задача состоит в том, чтобы определить наименьшее число
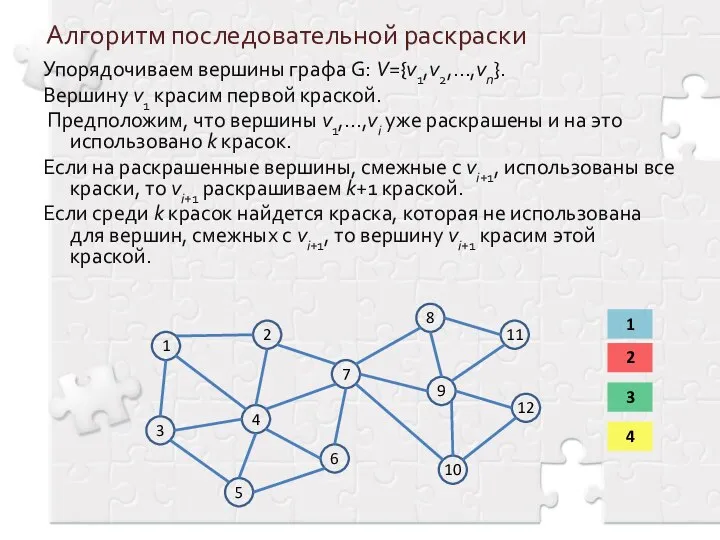
- 8. Алгоритм последовательной раскраски Упорядочиваем вершины графа G: V={v1,v2,…,vn}. Вершину v1 красим первой краской. Предположим, что вершины
- 9. Раскраска ребер Реберная раскраска называется правильной, если смежные ребра имеют различные цвета. Граф, доаускающий правильную реберную
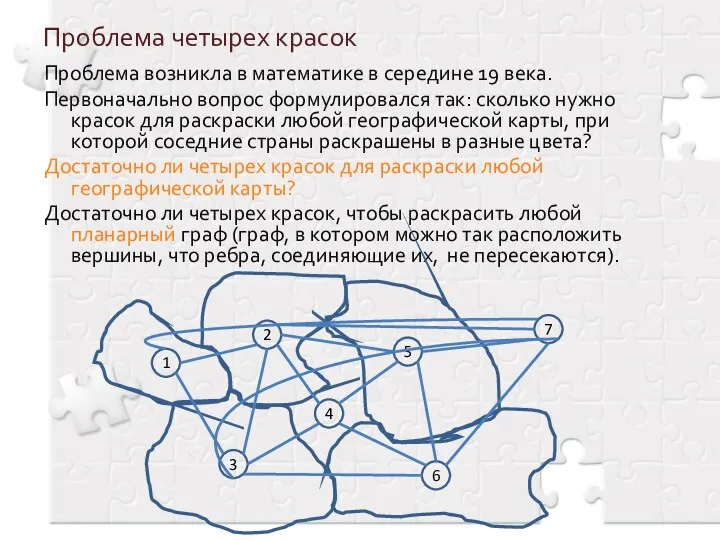
- 10. Проблема четырех красок Проблема возникла в математике в середине 19 века. Первоначально вопрос формулировался так: сколько
- 11. Проблема четырех красок Эта проблема вызвала большой интерес в математике. Есть свидетельства, что ей занимались известные
- 13. Скачать презентацию





 Некоторые законы распределения случайных величин. Нормальный закон распределения (закон Гаусса)
Некоторые законы распределения случайных величин. Нормальный закон распределения (закон Гаусса) Математика. Занятие 31
Математика. Занятие 31 Подобные треугольники. (8 класс)
Подобные треугольники. (8 класс) Числа 6 и 7. Письмо цифры 7 (1 класс)
Числа 6 и 7. Письмо цифры 7 (1 класс) Эквивалентные преобразования формул
Эквивалентные преобразования формул Численные методы решения систем линейных уравнений
Численные методы решения систем линейных уравнений Косинусоида. Задание № 9
Косинусоида. Задание № 9 Проценты. ОГЭ и ЕГЭ
Проценты. ОГЭ и ЕГЭ Треугольники. Задачи
Треугольники. Задачи Решение СЛАУ методом Крамера
Решение СЛАУ методом Крамера Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Устный счёт для дошкольников
Устный счёт для дошкольников Десятичные дроби произвольного знака
Десятичные дроби произвольного знака Вычитание смешанных чисел. 5 класс
Вычитание смешанных чисел. 5 класс Арифметический пейзаж
Арифметический пейзаж электронный учебник по интеллектике в 5 классе. знакомство с вероятностью
электронный учебник по интеллектике в 5 классе. знакомство с вероятностью Приближенные решения уравнений
Приближенные решения уравнений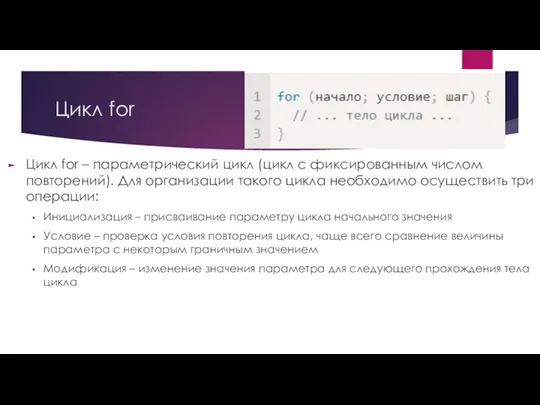 Цикл for
Цикл for Вторая производная и её физический смысл
Вторая производная и её физический смысл Max cut problem
Max cut problem Третий признак равенства треугольников. 7 класс
Третий признак равенства треугольников. 7 класс Тригонометрия (В5, В7) на ЕГЭ
Тригонометрия (В5, В7) на ЕГЭ Играем и считаем. Комплекс учебно-развивающих компьютерных игровых тренажеров по начальному обучению математике
Играем и считаем. Комплекс учебно-развивающих компьютерных игровых тренажеров по начальному обучению математике Параллельные прямые
Параллельные прямые Задача на арифметическую прогрессию (2)
Задача на арифметическую прогрессию (2)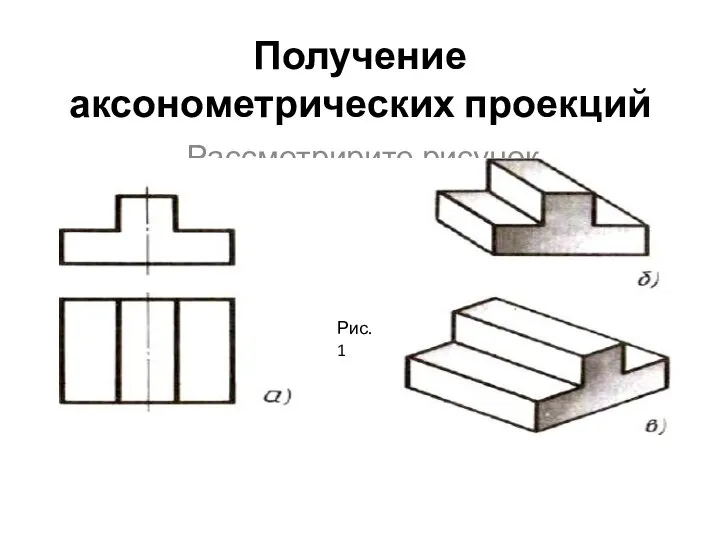 Получение аксонометрических проекций
Получение аксонометрических проекций Движение
Движение Виды кривых, замечательные кривые. Окружность и круг
Виды кривых, замечательные кривые. Окружность и круг