Физико-математические основы ОФЭКТ

Содержание
Излучение точечного источника. Закон Бера
Основная задача ОФЭКТ. Круговая геометрия измерений в ОФЭКТ. Влияние факторов геометрического ослабления и ослабления излучения веществом
Методы обращения интегрального экспоненциального преобразования Радона:
Метод двумерной фильтрации
Метод Фурье-синтеза
Метод одномерной фильтрации
Методы коррекции на поглощение. Метод корректирующей матрицы

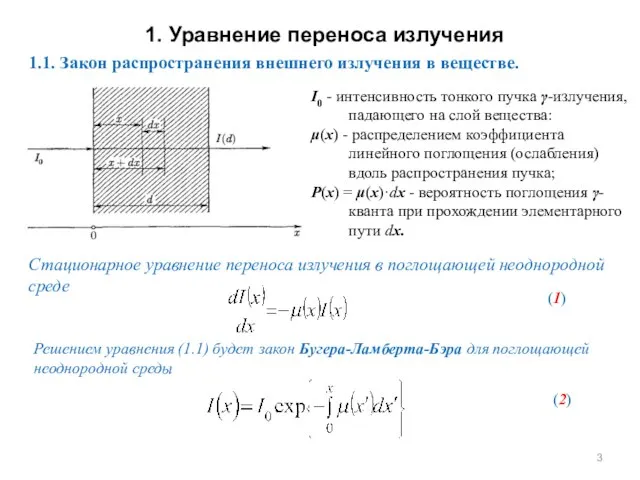
1. Уравнение переноса излучения
I0 - интенсивность тонкого пучка γ-излучения, падающего на слой вещества:
μ(x) - распределением коэффициента линейного поглощения (ослабления) вдоль распространения пучка;
P(x) = μ(x)·dx - вероятность поглощения γ-кванта при прохождении элементарного пути dx.
1.1. Закон распространения внешнего излучения в веществе.
Стационарное уравнение переноса излучения в поглощающей неоднородной среде
Решением уравнения (1.1) будет закон Бугера-Ламберта-Бэра для поглощающей неоднородной среды
(1)
(2)

1.2. Закон распространения излучения при действии внутренних источников излучения (самоизлучающие объекты)
I0 - интенсивность точечного источника, излучающего в телесный угол 4π;
μ(x) - распределением коэффициента линейного поглощения вдоль прямой, соединяющей источник с небольшой площадкой Δσ, наклоненной под
углом φ к этой прямой.
Тогда интенсивность I(x), приходящаяся на площадку Δσ, будет равна:
(3)
Выражение (1.3) учитывает четыре основных фактора:
геометрическое ослабление;
ослабление излучения в веществе;
наклон площадки детектора.

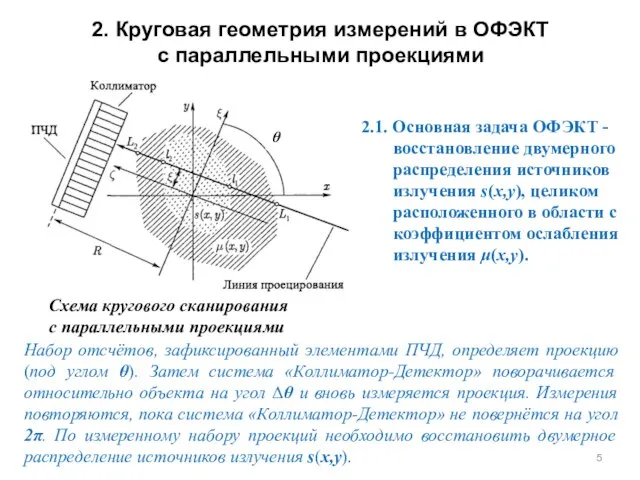
2. Круговая геометрия измерений в ОФЭКТ
с параллельными проекциями
2.1. Основная задача ОФЭКТ - восстановление двумерного распределения источников излучения s(x,y), целиком расположенного в области с коэффициентом ослабления излучения μ(x,y).
Набор отсчётов, зафиксированный элементами ПЧД, определяет проекцию (под углом θ). Затем система «Коллиматор-Детектор» поворачивается относительно объекта на угол Δθ и вновь измеряется проекция. Измерения повторяются, пока система «Коллиматор-Детектор» не повернётся на угол 2π. По измеренному набору проекций необходимо восстановить двумерное распределение источников излучения s(x,y).
Схема кругового сканирования
с параллельными проекциями

(5)
2.2. Выражение для проекции p(ξ,θ), измеренной под углом θ во вращающейся системе координат
Распределение источников излучения s(ξ,θ) :
Распределение линейного коэффициента поглощения μ(ξ,θ):
Тогда выражение для проекции p(ξ,θ) – интенсивность излучения, выходящего из объекта, будет иметь вид:
(4)

2.3. Влияние геометрического ослабления
и ослабления излучения веществом
2.3.1. Геометрическое ослабление
при равномерном распределении источников [sΘ(ξ,ϛ) = const = C] и отсутствии поглощения [μΘ(ξ,ϛ) = 0] равно:
Если не учитывать зависимость фактора геометрического ослабления от ϛ [т.е. (R - ϛ) = R], то получим:
Тогда относительный вклад учёта фактора ϛ при характерных размерах томографии головы человека (R = 25 см; l1 = -l2 = 8 см) составит:
т.е. геометрическое ослабление вносит искажения на уровне 10%.

2.3.2. Ослабление излучения веществом
при равномерном распределении источников [sΘ(ξ,ϛ) = const = C],
при равномерном распределении поглощения - [μΘ(ξ,ϛ) = const = μ]
и отсутствии геометрического фактора равно:
Если не учитывать поглощение излучения в веществе (т.е. μ = 0),
то получим:
Тогда относительный вклад учёта фактора поглощения излучения в веществе μ при характерных размерах L2 = 8 см; l1 = -l2 = 8 см), μ = 0.15 см-1 для источника 99mTc (Еγ = 140 кэВ) в мягких тканях человека составит:
т.е. относительный вклад фактора поглощения излучения в 16 раз больше вклада фактора геометрического ослабления. Следовательно, ослаблением излучения в веществе пренебречь нельзя.

Тогда уравнение для проекции примет следующий вид
(несущественные постоянные множители отброшены):
Если бы μ(x,y) = 0, то это выражение превратилось бы в преобразование Радона относительно s(x,y), к которому применимы методы, рассмотренные в трансмиссионной РКТ.
Если считать μ(x,y) неизвестной функцией, подлежащей определению [как и s(x,y)], то задача становится слишком сложной для решения, т.к. нужно по одной двумерной функции р(ξ,Θ) восстановить две двумерные функции - μ(x,y) и s(x,y). Возможное решение задачи – использование алгебраических методов.
Если считать μ(x,y) произвольной, но известной функцией (например, с помощью РКТ), то решение этой задачи возможно, по-видимому, только в алгебраической форме.

2.4. Вид экспоненциального преобразования Радона
Будем считать, что μ(x,y) = μ = const (промежуточный случай),
для которого найдено аналитическое решение.
Тогда:
Учитывая, что конфигурация области, ослабляющей излучение, известна (сам исследуемый объект), можно скорректировать каждую проекцию на постоянный для неё множитель ехр(-μL2).
Тогда уравнение ( 6) примет вид:
(6)
(7)
Т.к. s(x,y) = 0 вне интервала [l1; l2], пределы интегрирования можно продлить до бесконечности:

Это выражение называется экспоненциальным преобразованием Радона. С помощью δ-функции Дирака его можно представить в виде:
Целью коррекции ослабления излучения является получение из исходных проекций таких скорректированных проекций, которые совпадали бы с проекциями, полученными в отсутствие поглощающей среды. Тогда для обращения этих скорректированных проекций относительно s(x,y) можно применить методы, рассмотренные в трансмиссионной РКТ.
Большинство приближённых методов коррекции основаны на:
использовании оппозитных проекций [p(ξ,ϛ) и p(-ξ,Θ+π)].
методе корректирующей матрицы (не использующем оппозитные проекции), основанным на итерационном применении алгоритмов трансмиссионной РКТ с коррекцией ослабления излучения в каждой точке (пикселе) получаемого изображения.
(8)

3. Приближённые методы обращения
экспоненциального преобразования Радона.
3.1. Использование оппозитных проекций
Напомним выражения для прямой p(ξ,Θ) и оппозитной p(-ξ,Θ+π) проекций:
а при её наличии:
Пусть на линии проецирования находится только один
точечный источник s(ϛ) = Cδ(ϛ-ϛ0).
Тогда при отсутствии поглощающей среды [μ(x,y)=0]
прямая и оппозитная проекции равны:

Покажем, что выражение для скорректированной проекции ,
совпадающей с проекцией, полученной в отсутствие поглощающей среды, является среднее геометрическое значение, умноженное на известный множитель, равный
Существенно, что скорректированная проекция не зависит от позиции точечного источника на линии проецирования.

3.2. Метод корректирующей матрицы
Алгоритм использования корректирующей матрицы:
сначала восстанавливают «нулевое» приближение s0(х,у) к искомой функции s(х,у) по измеренным проекциям p(ξ,Θ) при помощи методов РКТ;
затем находят первое приближение s1(х,у) с использованием выбранных элементов матрицы с(х,у), корректирующей ослабление излучения в среде :
s1(х,у) = с(х,у)·s0(х,у)
где:
по найденному приближению s1(х,у) вычисляют проекции p1(ξ,Θ) и определяют их отклонение от измеренных проекций по формуле:
pl1(ξ,Θ) = p(ξ,Θ) - p1(ξ,Θ);
по этому отклонению находят элементы распределения sl1(х,у), также используя методы РКТ;
затем находят второе приближение s2(х,у) к искомой функции s(х,у) по формуле:
s2(х,у) = s1(х,у) + с(х,у)·sl1(х,у)
Затем процесс коррекции повторяется.
Как правило, процесс сходится за 1-2 итерации.

Определение корректирующей матрицы с(х,у).
Рассмотрим точечный источник s(х,у) = Cδ(х-х0)·δ(у-у0).
Запишем выражение для проекции (8) в виде:
Применим к проекциям метод фильтрованных обратных проекций для РКТ с фильтром Рамагандрана и Лакшминарайянана и получим:

Выполнив операцию обратного проецирования в точке [x0,y0] найдём:
(при ξ → ξ sinc[ ] → 1, a {sinc[ ] - sinc2[ ]/2} → 1/2

Определим элементы корректирующей матрицы с(х0,у0)·следующим образом:
Это выражение можно записать в дискретном виде:
где М – общее количество проекционных лучей,
проходящих через точку [x0,y0].
Фактически, с(хk,уj)·- величина, обратная среднеарифметическому от
[exp(-μlΘi)], которую можно подсчитать, зная μ и контуры L2 для всех [x,y].

КОНЕЦ 2-ОЙ ЧАСТИ
СПАСИБО ЗА ВНИМАНИЕ