Содержание
- 2. Определителем первого порядка матрицы называется число То есть:
- 3. Определителем второго порядка называется число, которое определяется по правилу:
- 4. Определителем третьего порядка называется число, которое определяется по правилу:
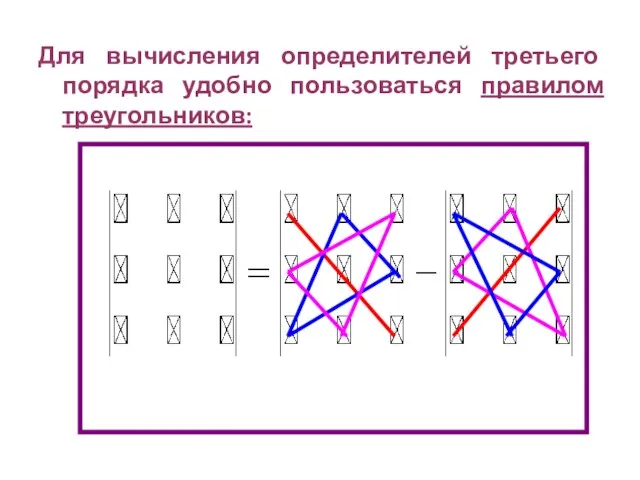
- 5. Для вычисления определителей третьего порядка удобно пользоваться правилом треугольников:
- 6. Пример. Вычислить определители матриц:
- 7. Решение:
- 8. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых
- 9. Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на (-1)S , где S –
- 10. В частности, минор элемента определителя третьего порядка найдется по правилу: Его алгебраическое дополнение:
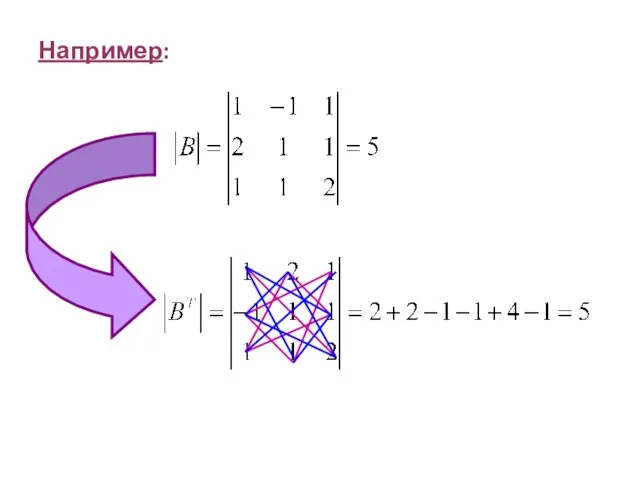
- 11. Свойства определителей 1 Определитель транспонированной матрицы равен определителю исходной матрицы.
- 12. Например:
- 13. 2 Перестановка двух строк или столбцов определителя эквивалентна умножению его на (-1).
- 14. Например: Меняем местами первую и вторую строки:
- 15. 3 Если определитель имеет две одинаковые строки или столбца, то он равен нулю.
- 16. Например:
- 17. 4 Общий множитель строки или столбца можно выносить за знак определителя.
- 18. Например: Выносим из второй строки множитель 2:
- 19. 5 Определитель не изменится, если к элементам одной строки или столбца прибавить соответственные элементы другой строки
- 20. Например: Первую строку умножаем на 2 и складываем со второй:
- 21. 6 Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения:
- 22. Пример. Вычислить определитель:
- 23. Раскладываем определитель по третьей строке: Решение: = Находим алгебраические дополнения:
- 25. Скачать презентацию




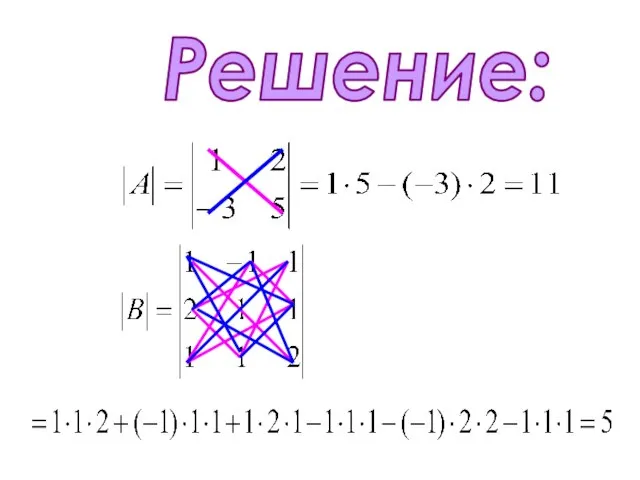















 Сумма углов треугольника
Сумма углов треугольника Ускоренное умножение
Ускоренное умножение Преобразование графиков функций. Приложение 2
Преобразование графиков функций. Приложение 2 Мишка. Тренажёр - раскраска
Мишка. Тренажёр - раскраска Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Презентация на тему Графический метод решения систем
Презентация на тему Графический метод решения систем  Пифагор Самосский
Пифагор Самосский Геометрические ребусы
Геометрические ребусы Математические понятия и их виды
Математические понятия и их виды Числа 1 - 4. (1 класс)
Числа 1 - 4. (1 класс) Математика, Устный счёт
Математика, Устный счёт 2_Teoria_veroyatnostey_920_is
2_Teoria_veroyatnostey_920_is Решение практико-ориентированных задач ОГЭ 2021г. Задачи про шины
Решение практико-ориентированных задач ОГЭ 2021г. Задачи про шины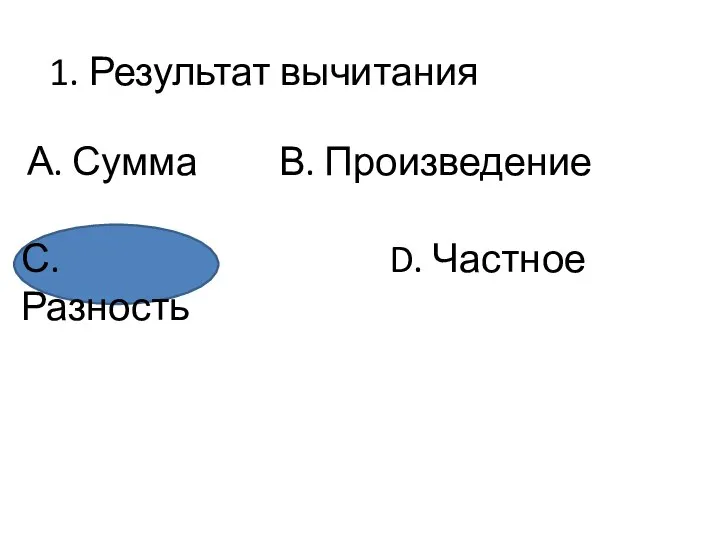 Игра
Игра Метод экспоненциального сглаживания
Метод экспоненциального сглаживания Математика и музыка
Математика и музыка Свойства функций. 9 класс
Свойства функций. 9 класс Решение треугольников
Решение треугольников Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Деление суммы на число
Деление суммы на число Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Линейные дискретные системы
Линейные дискретные системы Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля
Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля Сложение и вычитание без перехода через десяток
Сложение и вычитание без перехода через десяток Показательная функция
Показательная функция Понятие вектора в пространстве
Понятие вектора в пространстве Корни уравнения
Корни уравнения Квадратные корни. Обобщающий урок
Квадратные корни. Обобщающий урок