урок 1,2 по геометрии 11 класс 6 сентября 2022

Цели урока:
1) провести диагностику знаний учащегося;
2) повторить, систематизировать и обобщить знания по теме урока.

План урока
1. Организационный момент
2. Актуализация знаний учащихся
3. Теоретический тест с последующей самопроверкой
4. Решение задач
5. Подведение итогов и постановка домашнего задания

Ход урока
1. Орг. момент
2. Актуализация знаний учащихся
Учащийся самостоятельно 3 мин работает с учебником: с.4-7.
3. Теоретический тест с последующей самопроверкой
Ответы на тест: 1-д, 2-д, 3-в, 4-в, 5-б, 6-г, 7-а, 8-б, 9-д, 10-в.
Обсуждаются неправильные ответы. При необходимости оказывается консультация.
4. Решение задач
Сильный ученик работает самостоятельно. Учитель контролирует работу слабого учащегося, оказывая необходимую помощь.
5. Дом. задание: повторить пп. 2-3 (с.4-7); задачи 3, 4, 5.

Теоретический тест
1.Какое из следующих утверждений верно:
а) любые 4 точки лежат в 1-й плоскости; б) любые 3 точки лежат в 1-й плоскости; в) любые 4 точки не лежат в 1-й плоскости; г) через любые 3 точки проходит плоскость; д) через любые 3 точки, не лежащие на 1-й прямой, проходит плоскость и притом только одна.
2. Сколько общих точек могут иметь 2 различные плоскости? а) 2; б) 3; в) несколько; г)бесконечно много; д) бесконечно много или ни одной.
3. Точки А, В, С лежат на 1-й прямой, точка D не лежит на ней. Через каждые 3 точки проведена 1 плоскость. Сколько различных плоскостей при этом получилось? а) 2; б) 3; в) 1; г) 4; д) бесконечно много.
4. Если 3 точки не лежат на 1-й прямой, то положение плоскости в пространстве: а) не определяются в любом случае; б) определяются, но при определённых условиях; в) определяются в любом случае; г) ничего сказать нельзя; д) другой ответ.
5. Выбери верное:
а) если 1 точка прямой лежит в плоскости, то все точки прямой лежат в этой плоскости;
б) через прямую и не лежащую на ней точку проходит плоскость и притом только одна;
в) через 2 перекрещивающиеся прямые плоскость провести нельзя;
г) любые 2 плоскости не имеют общих точек;
д) если 4 точки не лежат в 1-й плоскости, то какие-нибудь 3 их них лежат на 1-й прямой.
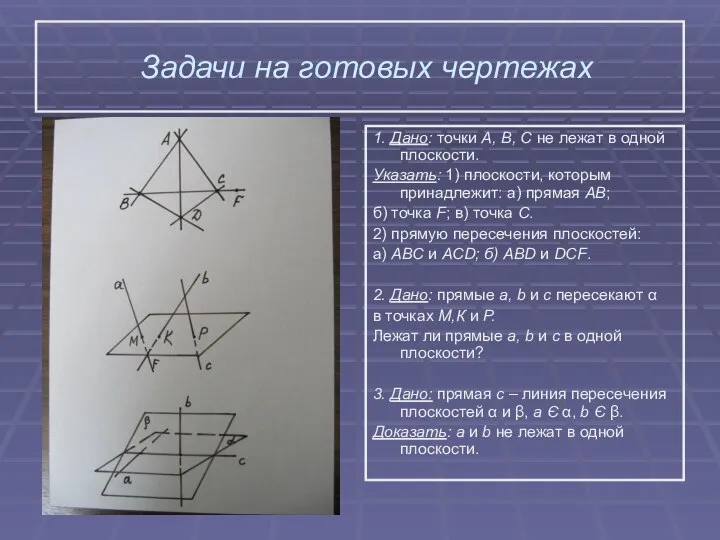
6. Назови общую прямую плоскостей AFD и DEF: a) AD; б) DE; в) определить нельзя; г) DF; д) AF.
7. Какую перечисленных плоскостей пересекает прямая ЕF? а) ABC; б) AA,D; в) BB,C,; г) AEF; д) B,C,C (см. рис.).
8. Через точку М, не лежащую на прямой а, провели прямые, пересекающие прямую а. Тогда: а) эти прямые не лежат в 1-й плоскости; б) эти прямые лежат в 1-й плоскости; в) никакого вывода сделать нельзя; г) часть прямых лежат в 1-й плоскости, а часть – нет; д) все прямые совпадают с прямой а.
9. Прямая а лежит в плоскости α и пересекает плоскость β. Каково взаимное расположение плоскостей α и β?
а) определить нельзя; б) они совпадают; в) имеют только 1 общую точку; г) не пересекаются; д) пересекаются по некоторой прямой.
10. Точки А, В, С не лежат на 1-й прямой. М Є АВ, К Є АС, Х Є МК. Выбери верное утверждение: а) Х Є АВ;
б) Х Є АС; в) Х Є АВС; г) Х и М совпадают; д) Х и К совпадают.

Задачи на готовых чертежах
1. Дано: точки А, В, С не лежат в одной плоскости.
Указать: 1) плоскости, которым принадлежит: а) прямая АВ;
б) точка F; в) точка С.
2) прямую пересечения плоскостей:
а) АВС и АCD; б) ABD и DCF.
2. Дано: прямые a, b и c пересекают α
в точках М,К и Р.
Лежат ли прямые a, b и c в одной плоскости?
3. Дано: прямая с – линия пересечения плоскостей α и β, a Є α, b Є β.
Доказать: a и b не лежат в одной плоскости.

Ответы и указания
2. Нет, только если бы M, K и P лежали бы на одной прямой.
3. Доказательство. Пусть это не так,
т. е. прямые a и b лежат в одной плоскости. Тогда прямая с принадлежит этой плоскости. Через прямые а и с можно провести единственную плоскость α, которой принадлежит и прямая b. Получили противоречие.

Домашние задачи
3. См. задачу из классной работы (для тех, кто не успел решить во время урока).
4. Дано: α ∩ β = а, А и В Є α, С Є β.
Построить: прямые пересечения плоскости АВС с плоскостями α и β.
5. Дано: М ¢ α, А, В, С Є α, F Є MB, E Є MA.
1) F Є α?
2) Может ли E Є α?
3) Указать прямую пересечения плоскостей:
а) α и МВА; б) АВМ и ВМС.
4) Принадлежит ли АС плоскости МВС?

Ответы на вопросы:
1) Определение векторов.
2) Равные векторы. Длина вектора.
3) Коллинеарные векторы.
4) Компланарные векторы.
5) Единичный вектор.
6) Координатные вектора.
7) Разложить данный вектор по координатным векторам.
8) Найти длины векторов и .
9) Определение скалярного произведения двух векторов.
10) Свойства скалярного произведения.

Задание с пропусками в записях
а)
б)
в) и коллинеарны, значит, = …;
г) если , , – неколлинеарные векторы, то = …;
д) = …;
е) соs α = …;
ж) если ┴ , то …;
з) < 0, то угол между векторами и – …;
и) если угол между векторами и – острый, то …

Ответы на задание с пропусками
а)
б)
в) и коллинеарны, значит, , где k – некоторое число,
г) если , и неколлинеарны, то ;
д) = | | · | | · соs ( ), = ,
е) соs α = , соs α = ,
ж) если ┴ , то = 0,
з) < 0, то угол между векторами и – тупой,
и) если угол между векторами и – острый, то > 0.

Индивидуальная работа по карточкам
1 уровень
Вычислить угол между прямыми AB и CD, если A(1; 1; 0), B(3; –1; 0), C(4; –1; 2), D(0; 1; 0).
2 уровень
Дано: ABCD – параллелограмм. A(–6; –4; 6),
B(6; –6; 2), C(10; 0; 4).
Найти координаты вершины D и угол между
векторами и .
3 уровень
Дано: МАВС – тетраэдр. М(2; 5; 7), А(1; –3; 2),
В(2; 3; 7), С(3; 6; 2).
Найти расстояние от точки М до точки О пересечения медиан ∆АВС.