Содержание
- 2. Цели: Изучение формулы Научиться решать задания с этой формулой
- 3. Различие состоит в том, что в линейной функции х в 1 степени, а в той, которую
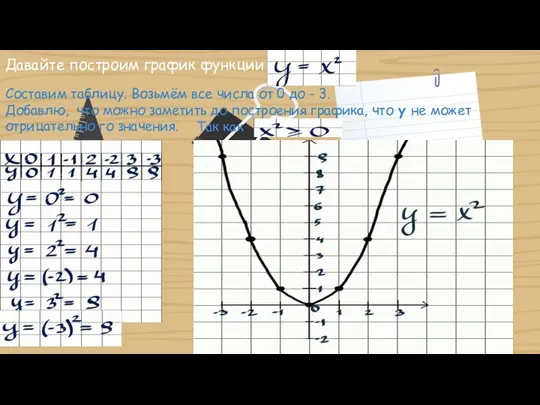
- 4. Давайте построим график функции Составим таблицу. Возьмём все числа от 0 до - 3. Добавлю, что
- 5. Откуда же появилась формула ? Если нам дан квадрат со стороной а, то его площадь мы
- 6. Пострив график, я могу сказать: Вершины параболы (0;0) Функция принимает только не отрицательные значения Наибольшее значение
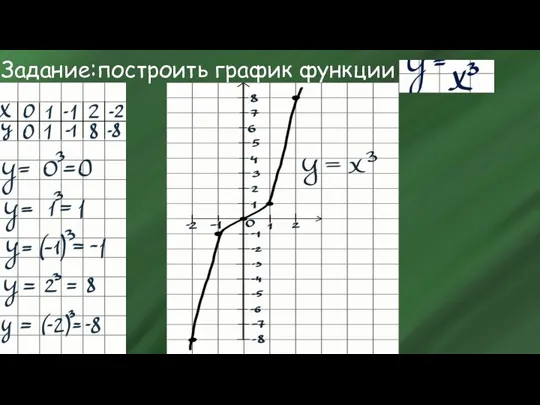
- 7. Задание:построить график функции
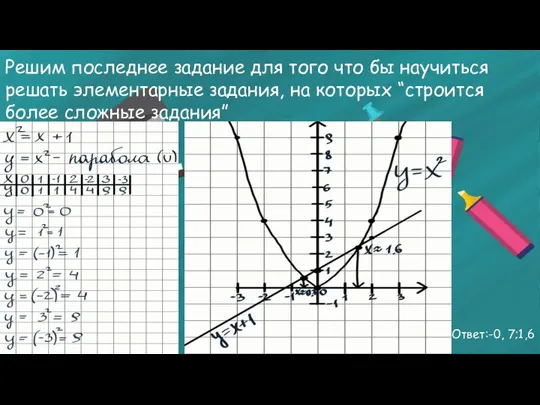
- 8. Решим последнее задание для того что бы научиться решать элементарные задания, на которых “строится более сложные
- 9. Вывод: Мы познакомились с функцией График выглядит как дугообразная прямая (парабола)
- 11. Скачать презентацию





 Преобразование выражений с помощью формул сокращенного умножения
Преобразование выражений с помощью формул сокращенного умножения Элементы теории вероятности
Элементы теории вероятности Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Решай, смекай, отгадывай!. Интерактивная математическая игра
Решай, смекай, отгадывай!. Интерактивная математическая игра Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла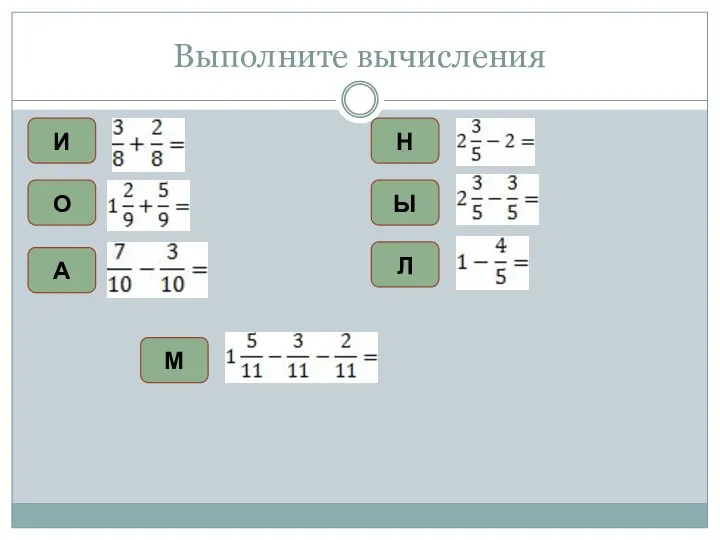 Выполните вычисления. 5 класс
Выполните вычисления. 5 класс Диагностическая работа по математике (октябрь)
Диагностическая работа по математике (октябрь) Метод Галеркина для дифференциально-операторного уравнения третьего порядка
Метод Галеркина для дифференциально-операторного уравнения третьего порядка Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Вычисления с многозначными числами
Вычисления с многозначными числами Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Окружность. Повторение
Окружность. Повторение Корреляционное моделирование
Корреляционное моделирование Тригонометрические функции
Тригонометрические функции Неполные квадратные уравнения
Неполные квадратные уравнения Перпендикулярность в пространстве. Тест. Практическая часть
Перпендикулярность в пространстве. Тест. Практическая часть Признаки классификации статистической сводки
Признаки классификации статистической сводки СРС 2 ВСК 2. Задачи
СРС 2 ВСК 2. Задачи Итоговое повторение. Алгебра. 8 класс
Итоговое повторение. Алгебра. 8 класс Тригонометрия. Учебно-игровое пособие
Тригонометрия. Учебно-игровое пособие Методы оптимальных решений
Методы оптимальных решений Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций Весёлая математика. Сколько в ширину? Сколько в высоту? Карточки для детей
Весёлая математика. Сколько в ширину? Сколько в высоту? Карточки для детей Контрольная
Контрольная Неравенство треугольника
Неравенство треугольника Признаки параллельности двух прямых
Признаки параллельности двух прямых Определение времени регулирования АС по переходной функции
Определение времени регулирования АС по переходной функции