Формулы сложения

Устная работа.
Какие знаки имеет синус, косинус, тангенс и котангенс в каждой из координатных четвертей?
Чему равен sin (- α) =
cos (- α) =
tg (- α) =
Чему равен sin (- 45) = sin (- π) =
cos (- 45) = cos (- ) =
tg (- 45) = tg (- 2π ) =

Устная работа.
а) Назовите формулу, выражающую связь между синусом и косинусом одного и того же угла.
б) Чему равно выражение
в) Как выражается тангенс угла через косинус того же угла?
г) Как выражается котангенс угла через синус того же угла?

Устная работа.

Устная работа.
Вычислить:
а) cos б) sin в)cos(-45)
г) sin(-30) д) cosπ +sinπ
е) sin2 (5α+β) + cos2 (5α+β)
ж) cos75°; з) cos15°.

Тема урока
Формулы сложения

Цель урока
вывести формулы сложения для косинуса суммы и разности углов, отработать их применение при вычислениях и выполнении преобразований тригонометрических выражений

Расстояние между двумя точками с заданными координатами:
Если А(х1;у1) и В(х2;у2), то
АВ2 = ( х2 – х1)2 + ( y2 – у1)2.
А(х1;у1)
В(х2;у2)

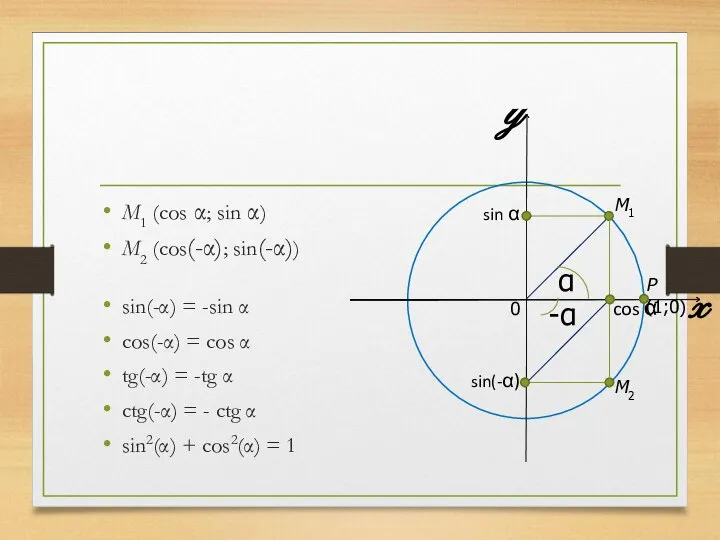
M1 (cos α; sin α)
M2 (cos(-α); sin(-α))
sin(-α) = -sin α
cos(-α) = cos α
tg(-α) = -tg α
ctg(-α) = - ctg α
sin2(α) + cos2(α) = 1
x
y
P (1;0)
0
α
-α
M2
M1
cos α
sin(-α)
sin α

Теорема
Для любых α и β справедливо равенство
cos(α + β) = cos α cos β – sin α sin β
По определению:
Mα (cos α; sin α)
M-β (cos(-β); sin(-β))
Mα+β (cos(α+β); sin(α+β))
∠M0OMα+β = ∠M-βOMα
⇒ △M0OMα+β = △M-βOMα
⇒ основания M0Mα+β = M-βMα равны
А значит равны (M-βMα)2 и (M0Mα+β)2, запишем их
x
y
M0(1;0)
0
Mα
M-β
Mα+β

Теорема
Имеем:
M0 (1; 0) M-β (cos(-β); sin(-β))
Mα (cos α; sin α) Mα+β (cos(α+β); sin(α+β))
(M0Mα+β)2 = (M-βMα)2
⇒ (1 - cos(α+β))2 +(sin(α+β))2 = (cos(-β) - cos α)2 + (sin(-β) - sin α)2
⇔ 1 - 2cos(α+β) + cos2(α+β) + sin2(α+β) = cos2 β - 2cos β cos α + cos2 α + sin2 β + 2sin β sin α + sin2 α
⇔ 2 - 2cos(α+β) = 2 - 2cos α cos β + 2sin α sin β
⇔ cos(α+β) = cos α cos β - sin α sin β
Теорема доказана.

Запомните!
cos(α + β) = cosα cosβ – sinαsinβ ;
Следствия:
cos(α - β) = cosα cosβ + sinα sinβ
sin(α + β) = sin α cos β + cos α sin β
sin(α - β) = sin α cos β - cos α sin β

Закрепление изученных формул.
№ 100-106 (нечетные)

7. Итоги урока
Итак, сегодня на уроке мы вывели формулы для нахождения косинуса суммы и разности двух углов, отработали навыки применения этих формул при вычислении и выполнении преобразований тригонометрических выражений, оценили уровень усвоения нового материала.