Формування математчних моделей електронних кіл

Класичний метод формування математичних моделей лінійних електронних кіл
Найпоширенішим є такий алгоритм формування математичної моделі електронного кола:
Побудувати еквівалентну розрахункову схему аналізованого кола, позначивши на ній усі компоненти та пронумерувавши всі вузли.
2. На еквівалентній розрахунковій схемі позначити взаємно узгоджені умовні додатні напрями струмів та напруг усіх гілок схеми.
3. Вибрати систему незалежних вузлів та незалежних контурів кола і записати систему топологічних лінійно незалежних рівнянь за першим та другим законами Кірхгофа.
4. Для кожного компонента схеми записати компонентне рівняння, враховуючи вибрані позначення умовних додатних напрямів струмів та напруг гілок еквівалентної розрахункової схеми.
5. Підставити компонентні рівняння у систему топологічних рівнянь і сформувати математичну модель аналізованого кола.

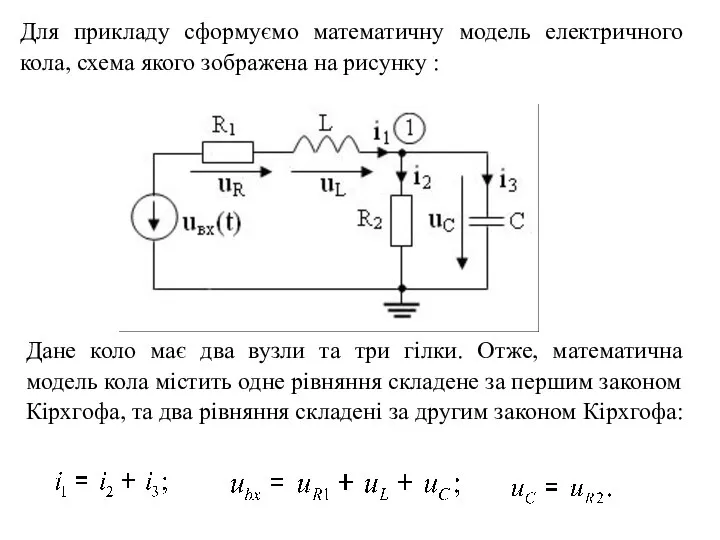
Для прикладу сформуємо математичну модель електричного кола, схема якого зображена на рисунку :
Дане коло має два вузли та три гілки. Отже, математична модель кола містить одне рівняння складене за першим законом Кірхгофа, та два рівняння складені за другим законом Кірхгофа:

де -
значення напруги на ємності у момент часу t = 0.
Компонентні рівняння елементів дорівнюють:
Підставивши у друге і третє рівняння компонентні рівняння,
отримуємо:
Для проведення аналізу кола потрібно дану систему інтегро-диференціальних рівнянь перетворити у одне рівняння, записане для одної вибраної змінної, після визначення якої можна відтак визначити інші невідомі змінні.

Продемонструємо це на прикладі двох варіантів вибору змінної: спочатку виберемо струм і1, який протікає через котушку індуктивності, а відтак виберемо напругу uc на ємності.
Варіант 1. Визначивши струми і2 та і3 через струм і1,отримуємо інтегро-диференціальне рівняння відносно струму і1:
Продиференціювавши його, після упорядкування отримуємо диференціальне рівняння другого порядку:

ПРИМІТКА. Визначення струмів і2 та і3 через струм і1 проводимо наступним чином:
Спочатку записуємо рівняння балансу напруг з урахуванням третього рівняння:
Звідси визначаємо струм :
Відтак визначаємо струм :
Цей вираз підставляємо в рівняння балансу напруг.

Варіант 2. Визначимо струми і1, і2, і3 через напругу uс на конденсаторі:
. Підставивши ці вирази у топологічні рівняння , після упорядкування отримуємо:
Наведені приклади свідчать про те, що в загальному випадку математична модель лінійного кола з постійними параметрами має вигляд лінійного диференціального рівняння з постійними коефіцієнтами. Викладений підхід до побудови математичних моделей електричних кіл з використанням компонентних рівнянь у диференціальній та інтегральній формах є класичним методом формування математичних моделей у вигляді інтегро-диференціальних або диференціальних рівнянь.

Узагальнюючи, приходимо до висновку, що математичну модель довільного лінійного кола можна записати у вигляді узагальненого лінійного неоднорідного диференціального рівняння n-го порядку. Якщо позначимо зовнішню дію на коло як х(t), а реакцію кола (вибраний струм чи напругу певної гілки) як у(t), тоді математична модель прийме вигляд:
де аn, аn-1, ...,a1, a0 - постійні коефіцієнти, які залежать від параметрів компонентів кола;
bm, bm-1, ... b1, b0 - постійні коефіцієнти, які залежать від параметрів зовнішньої дії та її похідних.
ПРИМІТКА:Порядок n диференціального рівняння характеризує порядок складності кола і дорівнює числу реактивних компонентів, енергетичний стан яких можна задати незалежно, про що буде іти мова далі.

Отже, задача аналізу лінійного електронного кола полягає у знаходженні розв’язку лінійного неоднорідного диференціального рівняння n-го порядку, тобто у визначенні миттєвих значень вибраного струму чи напруги у довільний момент часу.
Режими роботи електричних кіл
З курсу математики відомо, що загальний розв’язок лінійного неоднорідного диференціального рівняння є сумою двох складових, а саме : загального розв’язку однорідного рівняння, яке отримуємо , прирівнявши праву частину неоднорідного диференціального рівняння до нуля, і частинного розв’язку неоднорідного рівняння при заданій правій частині.

Загальний розв’язок однорідного рівняння відображає т.зв. вільні процеси, що відбуваються в колі при відсутності зовнішньої дії на коло, які спричинені наявністю запасів енергії, нагромадженої в реактивних компонентах кола. Характер цих процесів визначається лише топологією кола і параметрами компонентів. Цю складову називають вільною складовою. Аналіз показує, що оскільки параметри компонентів кола є додатними, то з бігом часу вільна складова загасає.
Частинний розв’язок неоднорідного диференціального рівняння при заданій правій частині відображає т.зв. вимушений режим, характер якого визначається характером зовнішньої дії на коло. Так, наприклад, якщо зовнішня дія є незмінною в часі, то вимушена складова розв’язку буде незмінним (постійним) струмом чи напругою. Якщо зовнішня дія є гармонічним коливанням, то вимушена складова також буде гармонічним коливанням тієї ж самої частоти. Якщо зовнішня дія є сумою декількох періодичних функцій, то вимушена складова розв’язку також буде сумою відповідних періодичних функцій. ).

Отже, загальний розв’язок неоднорідного диференціального рівняння має вигляд:
у(t)= увіл(t)+ увим(t).
Оскільки з бігом часу вільна складова загасає, то звідси випливає, що після загасання вільної складової у колі існує лише вимушена складова.
Режим роботи кола, в якому існує лише вимушена складова, що є сталою або періодичною функцією часу, чи сумою періодичних функцій часу, називають усталеним режимом. Зауважимо, що до усталених режимів належить також режим, в якому струми та напруги усіх гілок кола дорівнюють нулеві.
Своєю чергою, режим роботи кола, в якому існує вільна складова, називають перехідним режимом роботи кола від одного усталеного режиму до іншого, а процес такого переходу називають перехідним процесом.

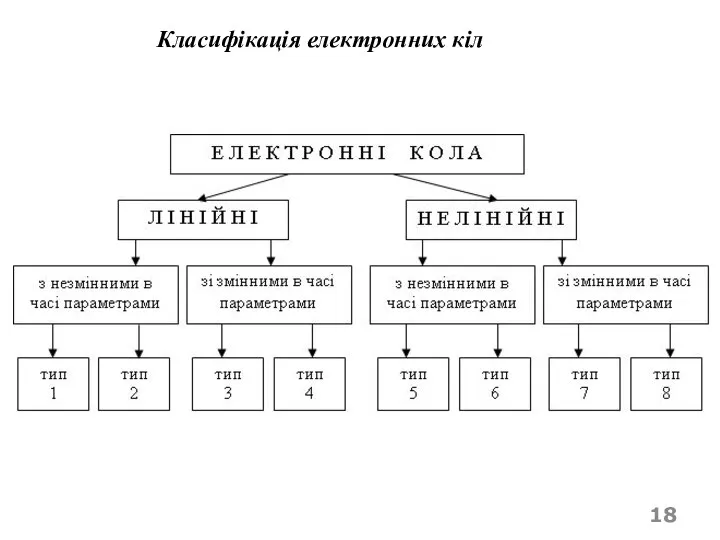
Класифікація електронних кіл та їх математичних моделей
Із викладеного раніше випливає, що вид математичної моделі електронного кола визначають моделі його компонентів і, зокрема, компонентні рівняння.
Електронні кола прийнято класифікувати за різними ознаками, які характеризують основні властивості кіл та впливають на методи їхнього аналізу. Найбільш загальною є така класифікація:
а) залежно від того, чи виконується в колі принцип суперпозиції (реакція кола на суму зовнішніх дій дорівнює сумі реакцій на кожну дію зокрема), електронні кола поділяють на:
- лінійні, в яких виконується принцип суперпозиції;
- нелінійні, в яких принцип суперпозиції не виконується;

б) залежно від того, чи параметри компонентів кола є незмінними (сталими) у часі, електронні кола поділяють на:
- стаціонарні, параметри яких не змінюються у часі (є сталими);
- нестаціонарні (параметричні) , параметри яких змінюються у часі.
Специфічною особливістю стаціонарних кіл є те, що довільна затримка в часі сигналу, поданого на вхід кола, спричиняє таку саму затримку вихідного сигналу без зміни його форми. Нестаціонарні (параметричні) кола такої властивості не мають, тобто затримка в часі сигналу, поданого на вхід кола, спричиняє зміну форми вихідного сигналу;

в) залежно від співвідношення між геометричними розмірами кола та довжиною хвилі електромагнітних коливань, які діють у колі, електронні кола поділяють на:
- кола із зосередженими параметрами, геометричні розміри яких менші від довжини хвилі сигналу, що поширюється в колі. У цих колах струм у всіх послідовно з’єднаних компонентах кола в конкретний момент часу є однаковим, а струми та напруги гілок кола залежать тільки від часу;
- кола із розподіленими параметрами, геометричні розміри яких (або хоча б один геометричний розмір кола) є більші або сумірні з довжиною хвилі. У таких колах часова затримка хоча б за однією з координат сумірна з періодом електромагнітних коливань, які діють у колі, а струми і напруги є функціями двох змінних - часу та координати х.

Математична модель кола (диференціальне рівняння) містить фундаментальну інформацію про характер процесів, що відбуваються у колі, та про властивості кола. Зокрема, для лінійних диференціальних рівнянь з постійними та змінними коефіцієнтами відома теорема накладання (теорема супер­позиції), на якій базується поширений в теорії кіл принцип накладання (принцип суперпозиції): реакція лінійного кола на складну зовнішню дію, яка являє собою лінійну комбінацію простіших дій, дорівнює лінійній комбінації реакцій, викликаних кожною простою дією зокрема. Застосування принципу накладання суттєво полегшує аналіз лінійних кіл і лежить в основі багатьох поширених методів аналізу.

Іншою важливою властивістю електронних кіл є здатність створювати в результаті перетворень сигналів коливання з новими частотами, які були відсутні у вхідному сигналі, тобто здатність перетворювати (трансформувати) частотний спектр. Аналіз показує, що наявність у складі кола хоча б одного нелінійного чи параметричного компонента є причиною перетворення спектра вхідного сигналу.

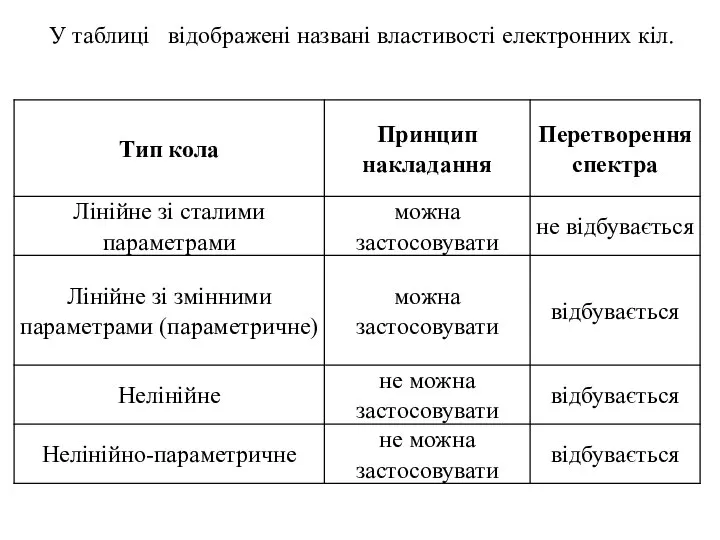
У таблиці відображені названі властивості електронних кіл.

Класифікація електронних кіл

Тип 1 - лінійні кола із зосередженими та незмінними у часі параметрами. Математичні моделі таких кіл є звичайними диференціальними рівняннями зі сталими коефіцієнтами;
Тип 2 - лінійні кола із розподіленими та незмінними у часі параметрами. Математичні моделі таких кіл є лінійними диференціальними рівняннями в частинних похідних;
Тип 3 - лінійні кола із зосередженими та змінними у часі параметрами (параметричні кола). Математичні моделі таких кіл є звичайними диференціальними рівняннями зі змінними коефіцієнтами;
Тип 4 - лінійні кола із розподіленими та змінними у часі параметрами. Математичні моделі таких кіл є лінійними диференціальними рівняннями в частинних похідних зі змінними в часі параметрами;