Содержание
- 2. План: Определение функции. Область определения. Область значений. Способы задания функции. Возрастание, убывание функции. Ограниченность функции. Наибольшее,
- 3. Из истории возникновения функции Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые
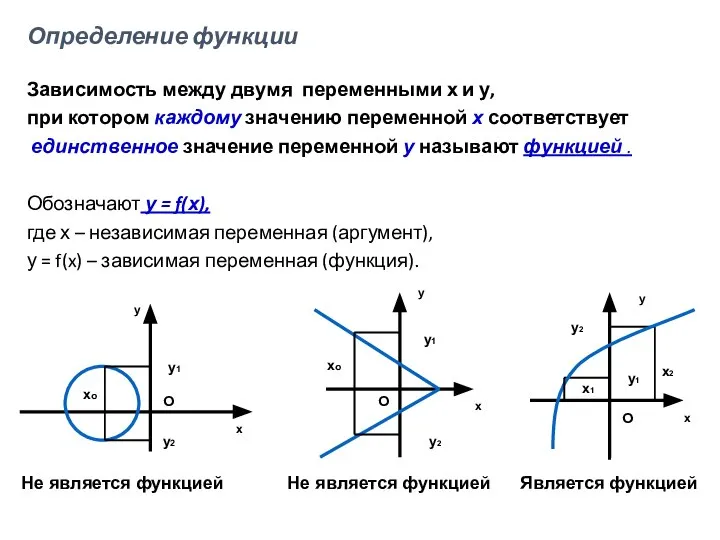
- 4. Определение функции Зависимость между двумя переменными х и у, при котором каждому значению переменной х соответствует
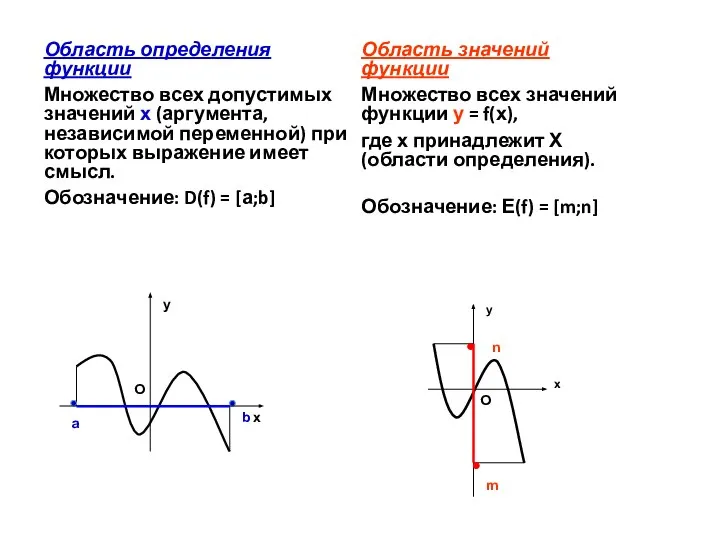
- 5. Область определения функции Множество всех допустимых значений х (аргумента, независимой переменной) при которых выражение имеет смысл.
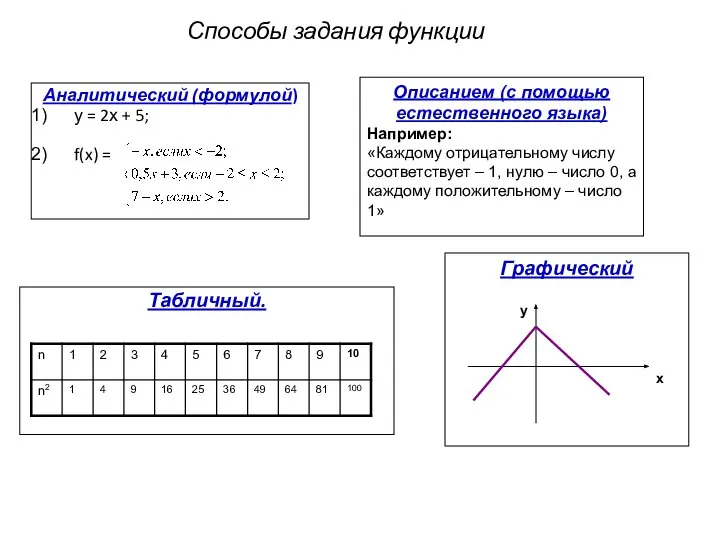
- 6. Способы задания функции Аналитический (формулой) у = 2х + 5; f(x) = Табличный. Описанием (с помощью
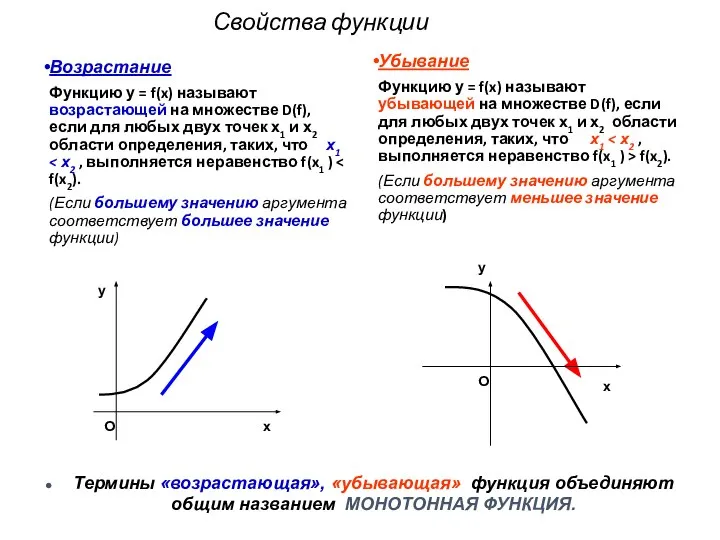
- 7. Свойства функции Возрастание Функцию у = f(x) называют возрастающей на множестве D(f), если для любых двух
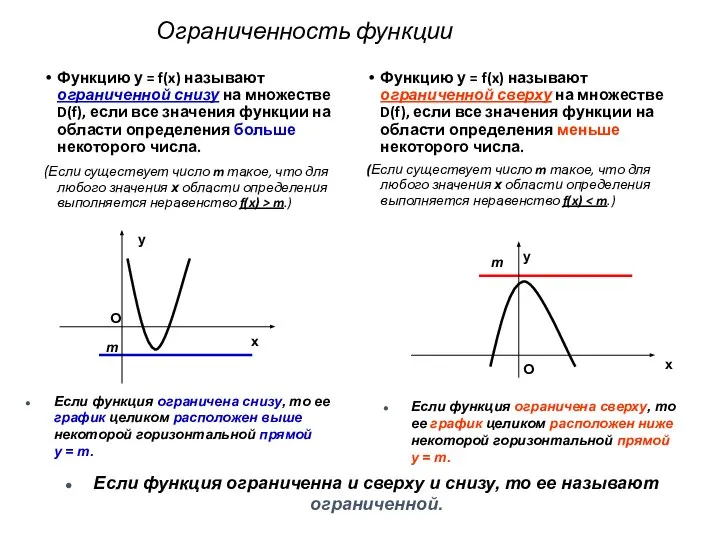
- 8. Ограниченность функции Функцию у = f(x) называют ограниченной снизу на множестве D(f), если все значения функции
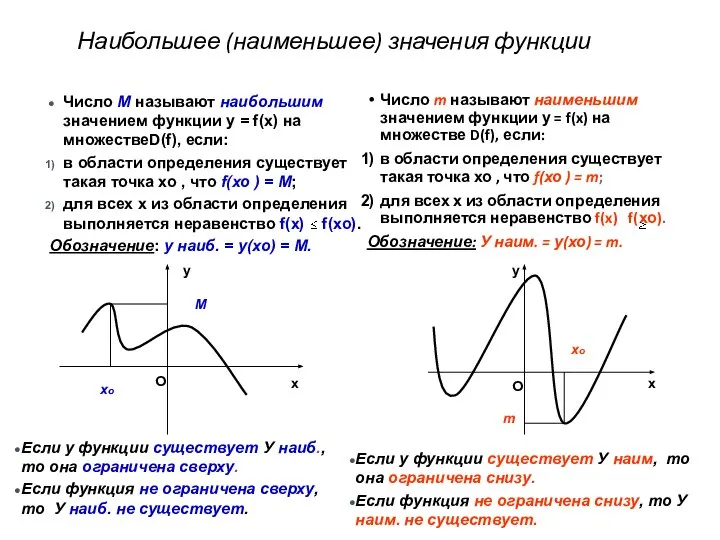
- 9. Наибольшее (наименьшее) значения функции Число m называют наименьшим значением функции у = f(x) на множестве D(f),
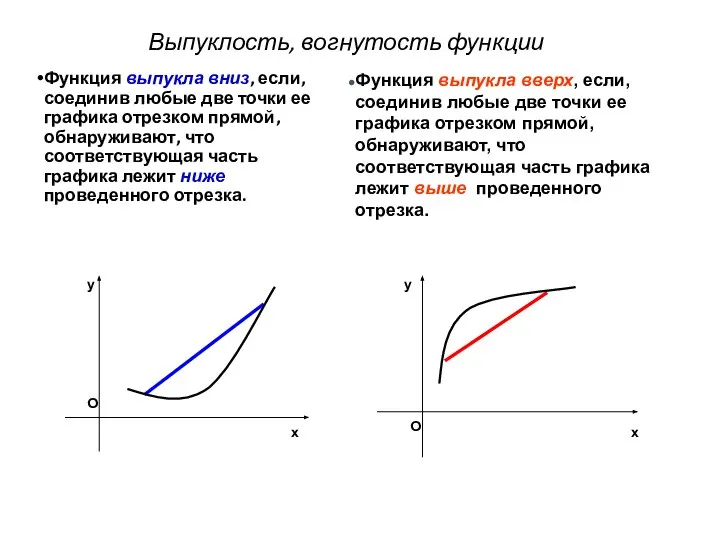
- 10. Выпуклость, вогнутость функции Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают,
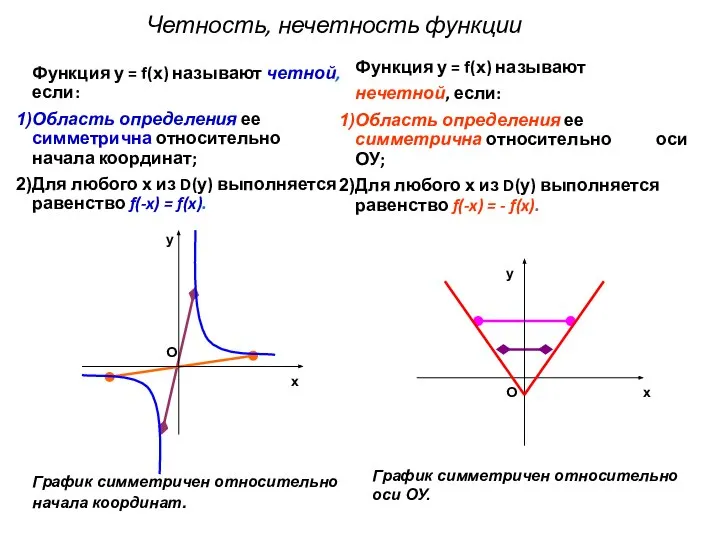
- 11. Четность, нечетность функции Функция у = f(х) называют четной, если: Область определения ее симметрична относительно начала
- 12. Алгоритм исследования функции Область определения. Область значений. Четность, нечетность функции. Возрастание, убывание функции. Ограниченность функции. Наибольшее,
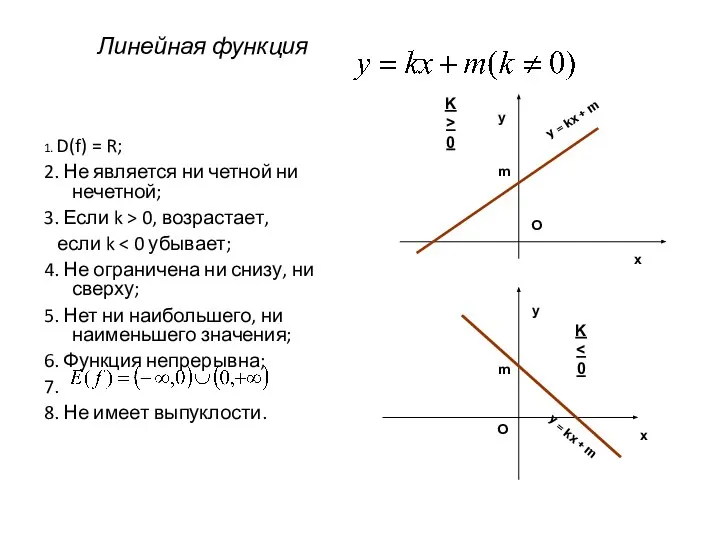
- 13. Линейная функция 1. D(f) = R; 2. Не является ни четной ни нечетной; 3. Если k
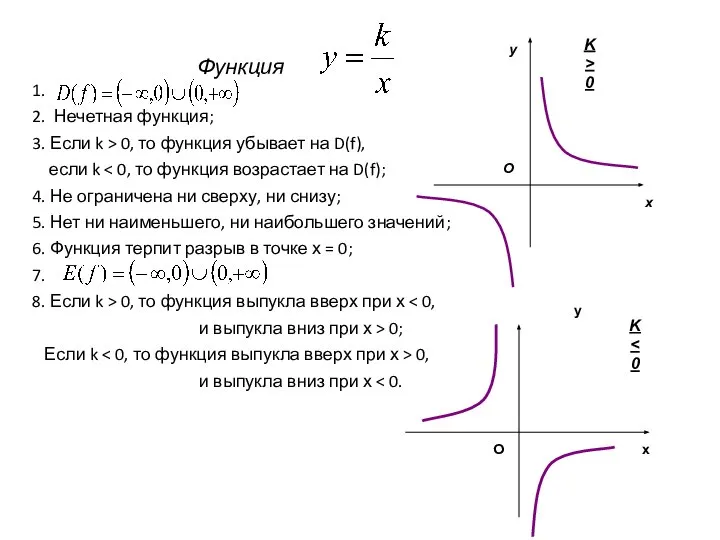
- 14. Функция 1. 2. Нечетная функция; 3. Если k > 0, то функция убывает на D(f), если
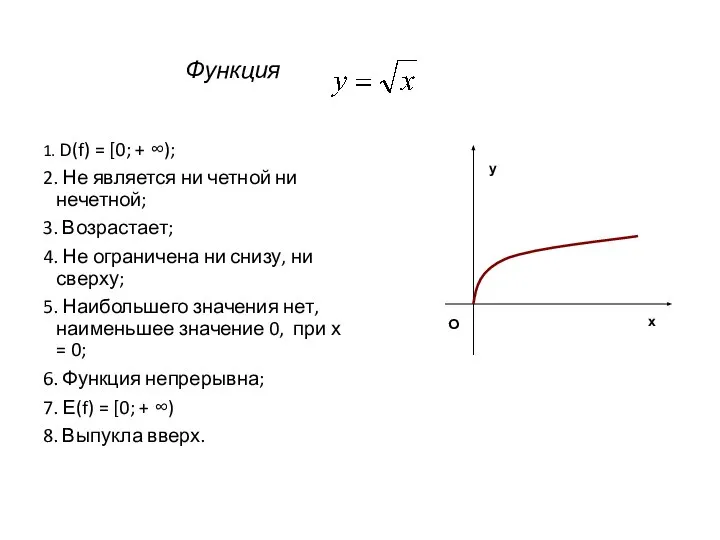
- 15. Функция 1. D(f) = [0; + ∞); 2. Не является ни четной ни нечетной; 3. Возрастает;
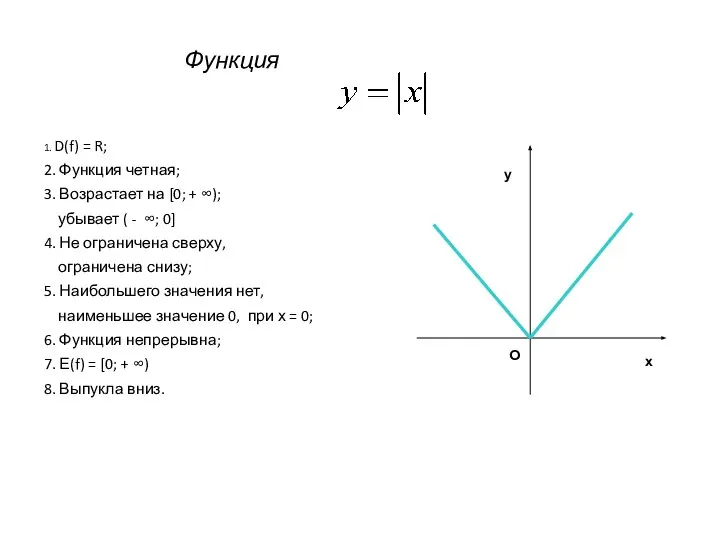
- 16. Функция 1. D(f) = R; 2. Функция четная; 3. Возрастает на [0; + ∞); убывает (
- 18. Скачать презентацию



 Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша
Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша Приемы вычитания с переходом на десяток
Приемы вычитания с переходом на десяток Функция y=ctg x. График
Функция y=ctg x. График Матрицы и определители
Матрицы и определители Дифференциальное исчисление в нормированных пространствах
Дифференциальное исчисление в нормированных пространствах Элементы теории обобщенных функций
Элементы теории обобщенных функций ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Механический смысл производной. Задания для устного счета
Механический смысл производной. Задания для устного счета Умножение. Координаты точки
Умножение. Координаты точки Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества
Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества Решение задач на дроби
Решение задач на дроби Равенство
Равенство Случаи вычитания 11-
Случаи вычитания 11- Веселые ромашки
Веселые ромашки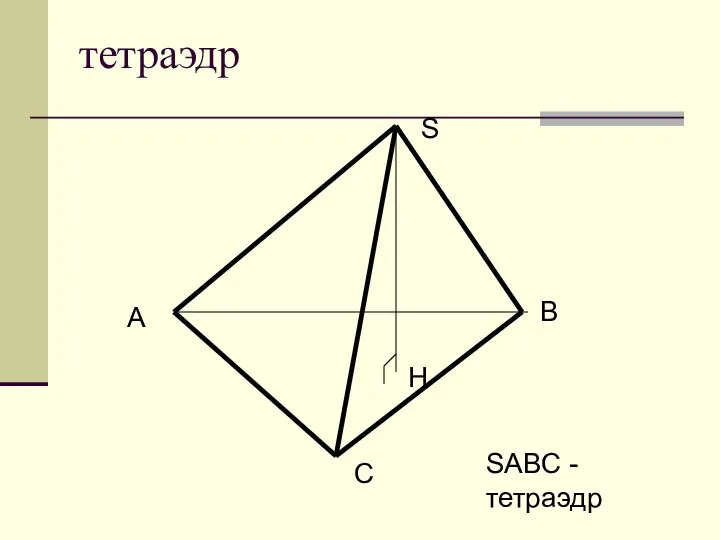 Тетраэдр
Тетраэдр Векторы. Направление вектора
Векторы. Направление вектора Изоморфные графы
Изоморфные графы Функция распределения дискретной случайной величины
Функция распределения дискретной случайной величины Игры. Памятка
Игры. Памятка Многоугольники в жизни
Многоугольники в жизни Методический материал по алгебре
Методический материал по алгебре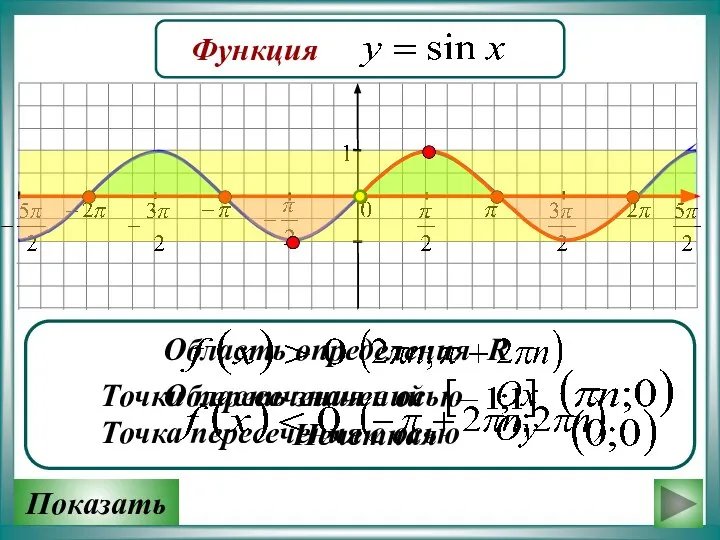 График функции y = sin x
График функции y = sin x Путешествие по морям
Путешествие по морям Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Площадь параллелограмма
Площадь параллелограмма Смежные углы
Смежные углы Сложение целых чисел
Сложение целых чисел Понятие интеграла
Понятие интеграла