Содержание
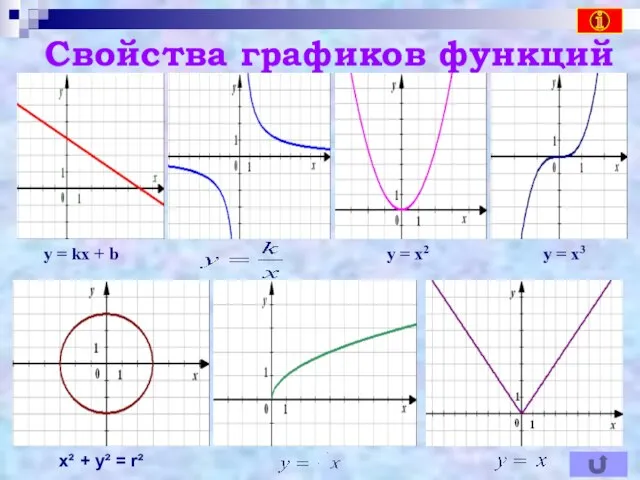
- 2. Свойства графиков функций у = х2 y = kx + b у = х3 х² +
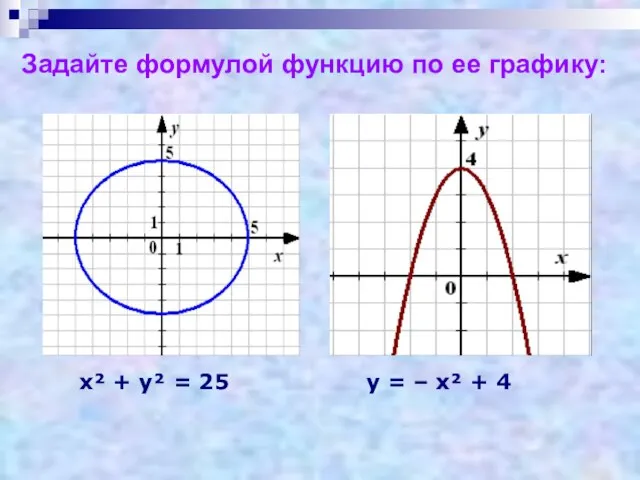
- 3. Задайте формулой функцию по ее графику: х² + у² = 25 у = – х² +
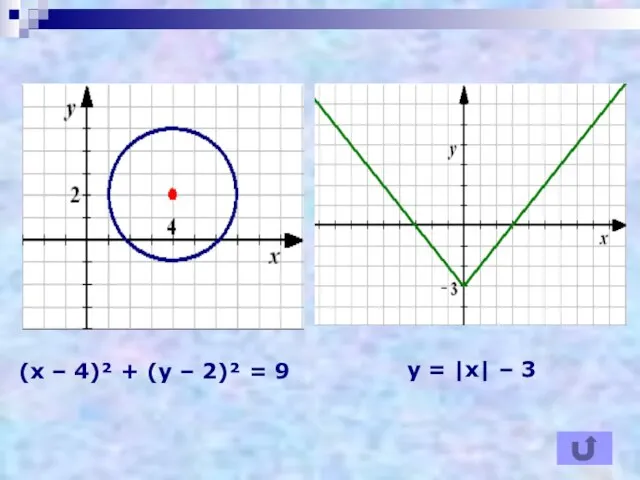
- 4. (х – 4)² + (у – 2)² = 9 у = |х| – 3
- 5. График функции – множество всех точек плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим
- 6. Функция линейная Формула у = kx + b, k – угловой коэффициент прямой График прямая (две
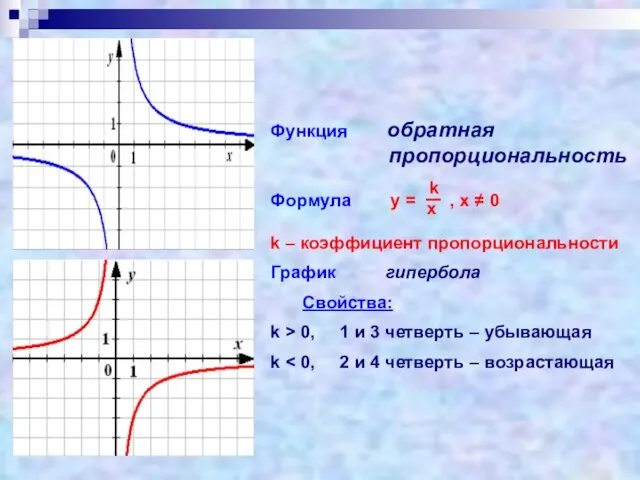
- 7. Функция обратная пропорциональность Формула у = , х ≠ 0 k – коэффициент пропорциональности График гипербола
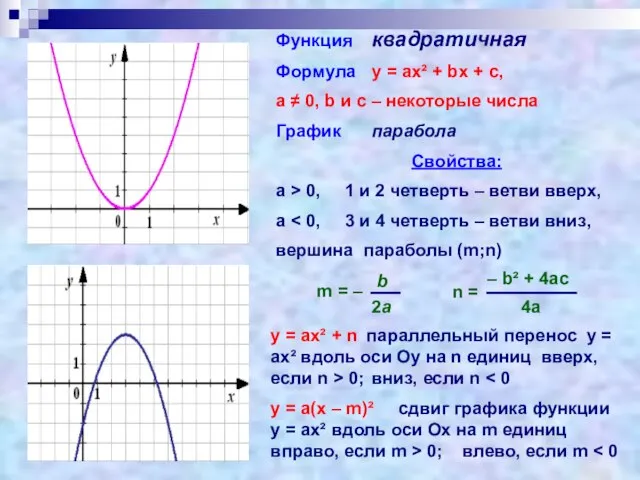
- 8. Функция квадратичная Формула у = ах² + bх + с, а ≠ 0, b и с
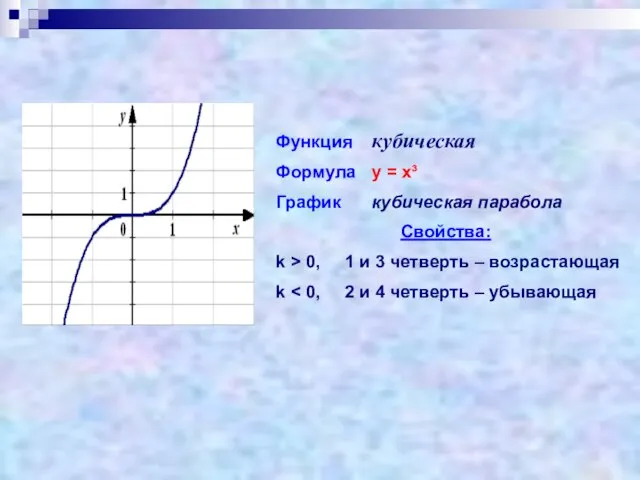
- 9. Функция кубическая Формула у = х³ График кубическая парабола Свойства: k > 0, 1 и 3
- 10. Формула (х – х0)² + (у – у0)² = r² (х; у) – координаты точки окружности
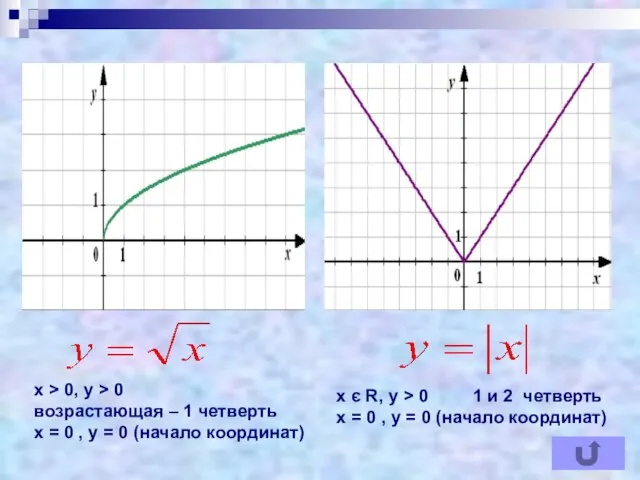
- 11. х > 0, у > 0 возрастающая – 1 четверть х = 0 , у =
- 12. Степень целого уравнения Если левая часть уравнения с двумя переменными представляет собой многочлен стандартного вида, а
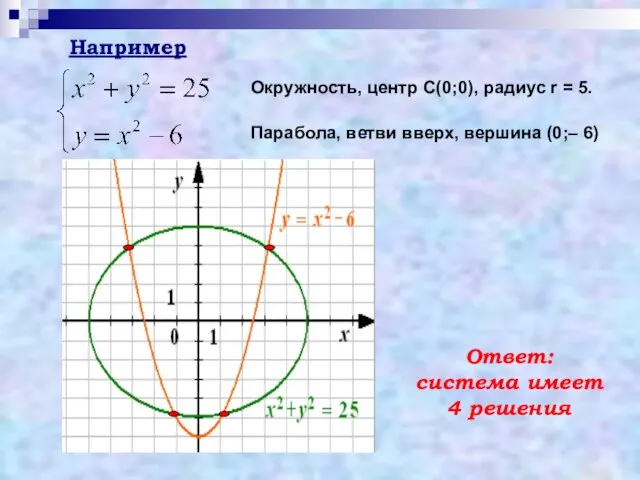
- 13. Например Окружность, центр С(0;0), радиус r = 5. Парабола, ветви вверх, вершина (0;– 6) Ответ: система
- 14. Алгоритм решения систем уравнений графически: 1. Выразить у через х в каждом уравнении (кроме уравнения окружности).
- 15. УСТНО: 1. Является ли пара чисел (-1; 3) решением уравнения а) х² - у + 2
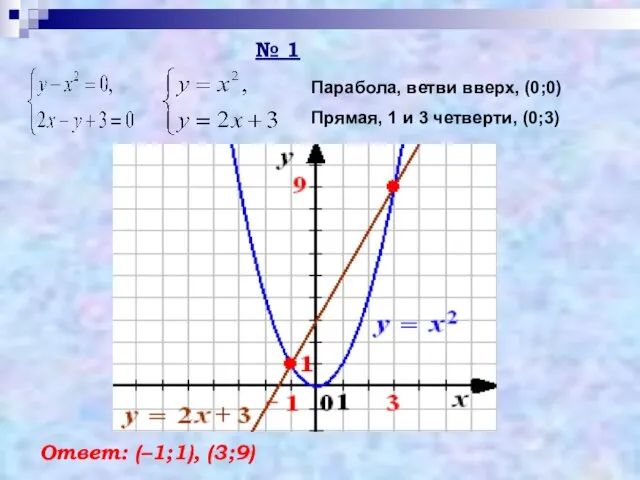
- 16. № 1 Парабола, ветви вверх, (0;0) Прямая, 1 и 3 четверти, (0;3) Ответ: (–1;1), (3;9)
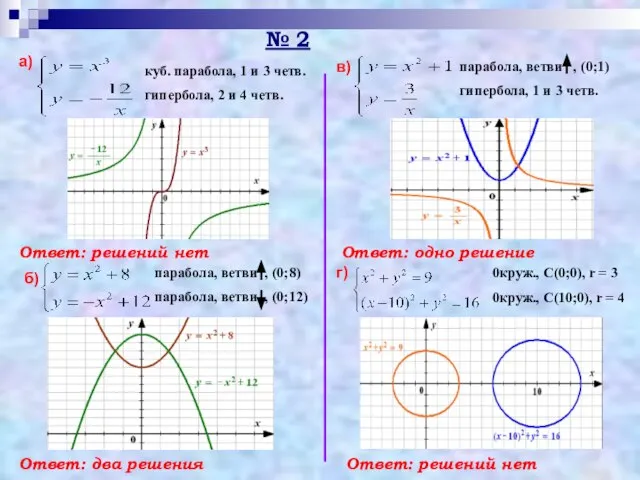
- 17. № 2 а) куб. парабола, 1 и 3 четв. гипербола, 2 и 4 четв. б) в)
- 19. Скачать презентацию






 Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"  Сложение дробей
Сложение дробей Пифагор и его теорема
Пифагор и его теорема Скалярное произведение векторов
Скалярное произведение векторов Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году
Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году Применение графов
Применение графов Элементы аналитической геометрии. Векторы
Элементы аналитической геометрии. Векторы Устный счёт. Закрепление изученного
Устный счёт. Закрепление изученного Морской бой
Морской бой Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Циліндр. Елементи циліндра
Циліндр. Елементи циліндра Игра
Игра Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся Л 8 Предел функции
Л 8 Предел функции Формулы для радиусов вписанной и описанной окружностей треугольника
Формулы для радиусов вписанной и описанной окружностей треугольника Производная и исследование функции
Производная и исследование функции Технология подготовки учащихся к овладению решения задач с параметрами комбинированными методами. Занятие №5
Технология подготовки учащихся к овладению решения задач с параметрами комбинированными методами. Занятие №5 Угол. Виды углов. Опрос
Угол. Виды углов. Опрос Применение векторов к решению задач
Применение векторов к решению задач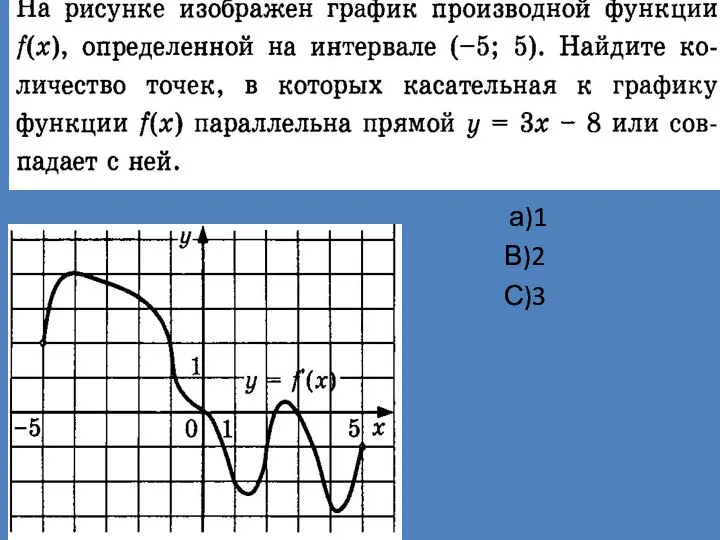 График производной функции
График производной функции Решаем задачи
Решаем задачи Устный счёт. 3 класс
Устный счёт. 3 класс Многогранники (задания)
Многогранники (задания) Решение задач при помощи уравнений
Решение задач при помощи уравнений Отрицательные числа в географии
Отрицательные числа в географии Признаки существования предела
Признаки существования предела Конкурс капитанов
Конкурс капитанов Взаимно обратные числа
Взаимно обратные числа