График квадратичной функции, содержащей переменную под знаком абсолютной величины

Основные определения и свойства
Функция, определяемая формулой у=ах²+вх+с, где х и у переменные, а параметры а, в и с – любые действительные числа, причём а≠0, называется квадратичной.
Абсолютной величиной неотрицательного числа называется само это число, абсолютной величиной отрицательного числа называется противоположное ему положительное число.
Свойства:
1.|a| ≥0,
2. |a|²= a²,
3.|a∙b|=|a|∙|b|,
4. |a/b|=|a|/|b|, b≠0

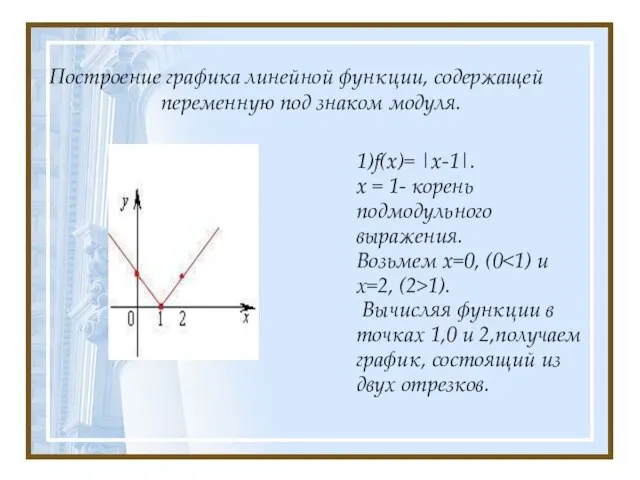
Построение графика линейной функции, содержащей
переменную под знаком модуля.
1)f(x)= |x-1|.
x = 1- корень
подмодульного
выражения.
Возьмем x=0, (0<1) и
х=2, (2>1).
Вычисляя функции в
точках 1,0 и 2,получаем
график, состоящий из
двух отрезков.

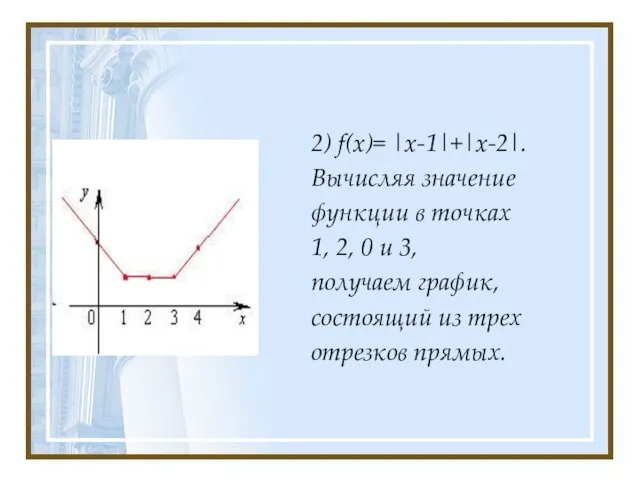
2) f(x)= |x-1|+|x-2|.
Вычисляя значение
функции в точках
1, 2, 0 и 3,
получаем график,
состоящий из трех
отрезков прямых.

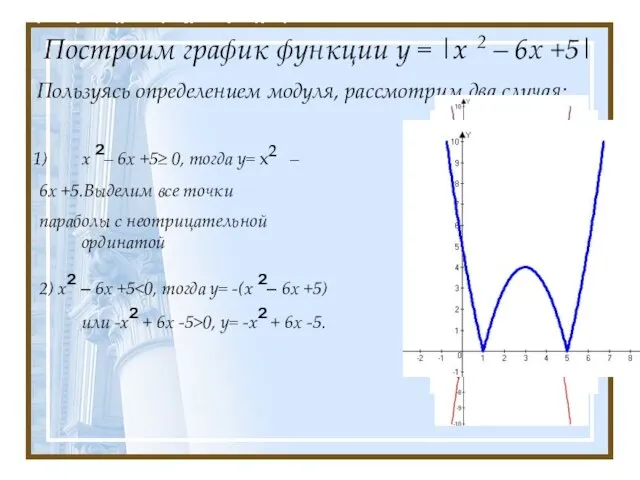
Построение графика квадратичной функции, содержащей переменную под знаком модуля
На примере функции у = x ²-6х +5 рассмотрим
всевозможные случаи расположения модуля.
у = |x 2 – 6х +5|
у = | х | 2 – 6х +5
у = х² – 6|х| +5
у = |х|² - 6|х|+5
у = |х² – 6х| +5
у = |х² – 6|х| +5|
у = x 2 -|6х + 5|
|y|= x 2 – 6х +5

Построим график функции у = |x 2 – 6х +5|
Пользуясь определением модуля, рассмотрим два случая:
Пользуясь определением модуля, рассмотрим два случая:
Пользуясь определением модуля, рассмотрим два случая:
Пользуясь определением модуля, рассмотрим два случая:
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
Выделим все точки параболы с неотрицательной ординатой.
x ²– 6х +5≥ 0, тогда у= x² –
6х +5.Выделим все точки
параболы с неотрицательной ординатой.
2) x² – 6х +5<0, тогда у= -(x ²– 6х +5) или -x² + 6х -5>0, y= -x² + 6х -5.

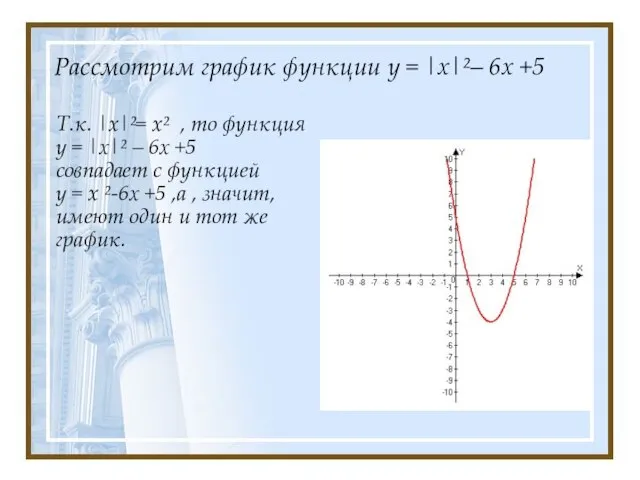
Рассмотрим график функции у = |х|²– 6х +5
Т.к. |x|²= x² , то функция у = |х|² – 6х +5
совпадает с функцией
у = x ²-6х +5 ,а , значит,
имеют один и тот же график.

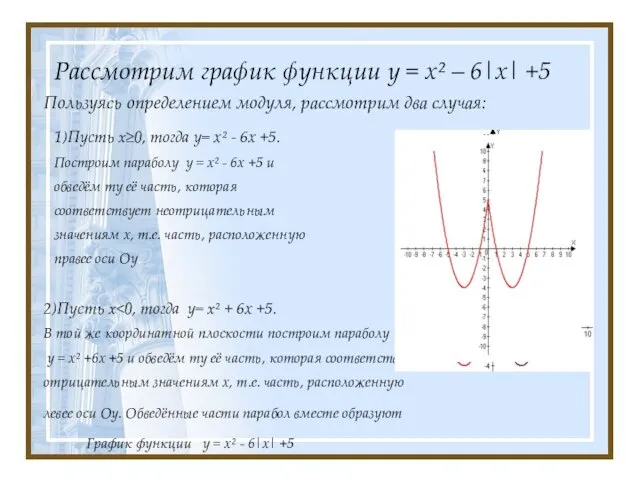
Рассмотрим график функции у = х² – 6|х| +5
Пользуясь определением модуля, рассмотрим два случая:
1)Пусть x≥0, тогда y= х² - 6х +5.
Построим параболу у = х² - 6х +5 и
обведём ту её часть, которая
соответствует неотрицательным
значениям х, т.е. часть, расположенную
правее оси Оу.
2)Пусть x<0, тогда y= x² + 6х +5.
В той же координатной плоскости построим параболу
у = х² +6х +5 и обведём ту её часть, которая соответствует
отрицательным значениям х, т.е. часть, расположенную
левее оси Оу. Обведённые части парабол вместе образуют График функции у = х² - 6|х| +5

Рассмотрим график функции
у = |х|² - 6|х|+5.
Т.к. |x|²= x² , то функция у = |х|² – 6|х| +5
совпадает с функцией у = x ²-6|х| +5
(см пред. пример)

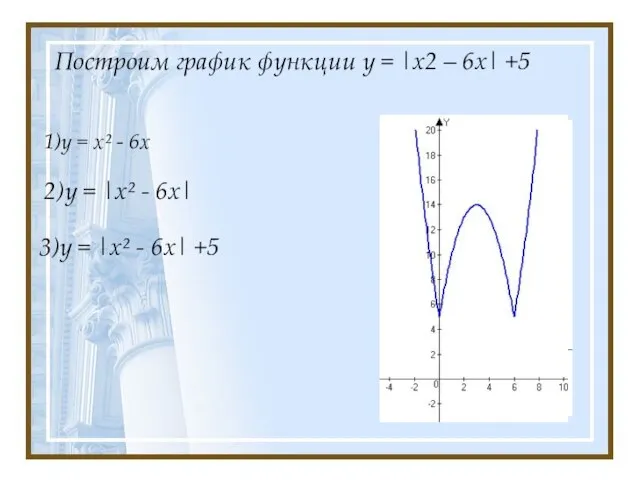
Построим график функции у = |х2 – 6х| +5
1)у = х² - 6х
2)у = |х² - 6х|
3)у = |х² - 6х| +5

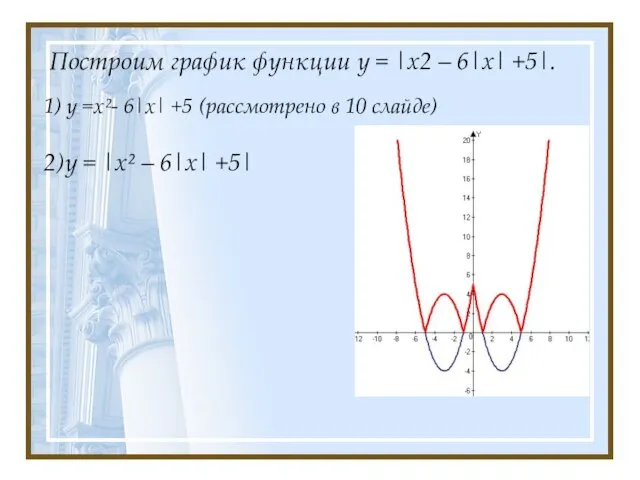
Построим график функции у = |х2 – 6|х| +5|.
1) у =х²- 6|х| +5 (рассмотрено в 10 слайде)
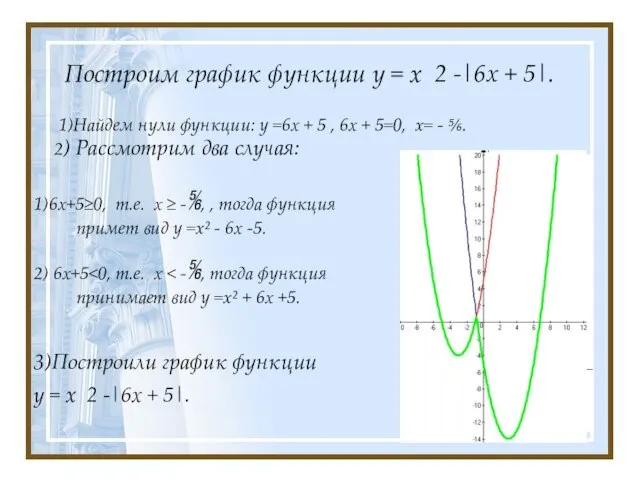
2)у = |х² – 6|х| +5|

Построим график функции у = x 2 -|6х + 5|.
1)Найдем нули функции: у =6х + 5 , 6х + 5=0, x= - ⅚.
2) Рассмотрим два случая:
1)6х+5≥0, т.е. х ≥ -⅚, , тогда функция примет вид у =x² - 6х -5.
2) 6х+5<0, т.е. х < -⅚, тогда функция принимает вид у =x² + 6х +5.
3)Построили график функции у = x 2 -|6х + 5|.

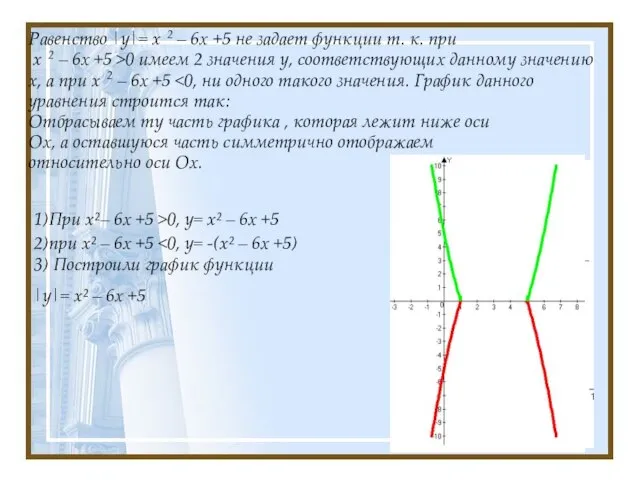
Равенство |y|= x 2 – 6х +5 не задает функции т. к. при
x 2 – 6х +5 >0 имеем 2 значения y, соответствующих данному значению
x, а при x 2 – 6х +5 <0, ни одного такого значения. График данного
уравнения строится так:
Отбрасываем ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отображаем
относительно оси Ох.
1)При x²– 6х +5 >0, y= x² – 6х +5
2)при x² – 6х +5 <0, y= -(x² – 6х +5)
3) Построили график функции
|y|= x² – 6х +5

Выводы:
1)Для построения графика функции y = |f(x)| , надо сохранить ту часть графика функции y = f(x), точки которой находятся на оси Ох или выше оси Ох, и симметрично отразить относительно оси Ох ту часть графика функции y = f(x), которая расположена ниже оси Ох.
2) Для построения графика y = f(|x|) надо сохранить ту часть графика функции y = f(|x|), точки которой на оси Оу или справа от неё и симметрично отразить эту часть графика относительно оси Оу.
3) Чтобы построить график уравнения |y|= f(x) нужно:
Отбросить ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отобразить
относительно оси Ох

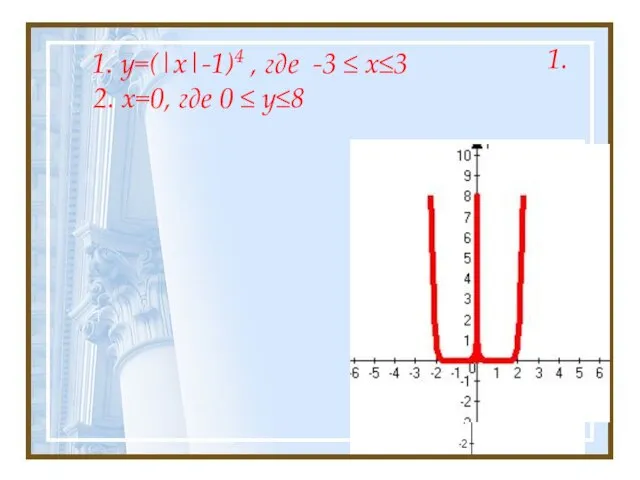
1. y=(|x|-1)4 , где -3 ≤ x≤3
2. x=0, где 0 ≤ у≤8
1.

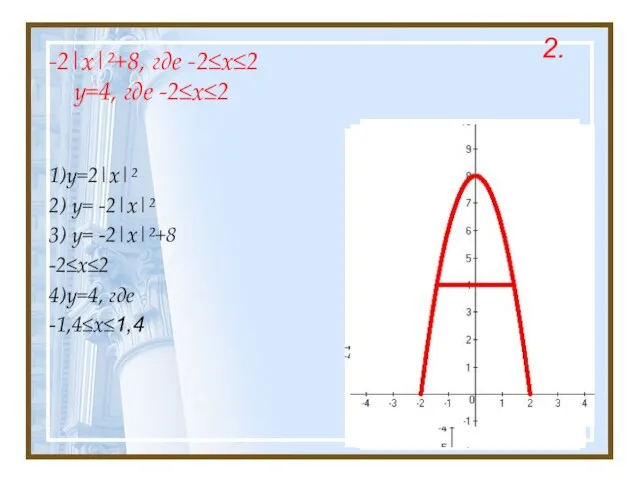
-2|x|²+8, где -2≤x≤2
y=4, где -2≤x≤2
1)y=2|x|²
2) y= -2|x|²
3) y= -2|x|²+8
-2≤x≤2
4)y=4, где
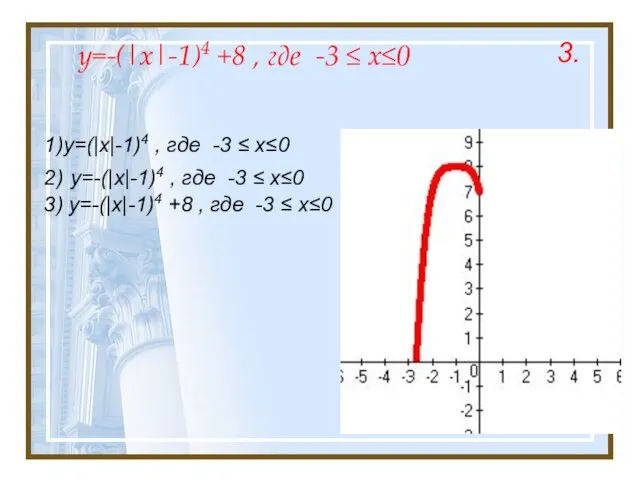
-1,4≤x≤1,4
2.

y=-(|x|-1)4 +8 , где -3 ≤ x≤0
1)y=(|x|-1)4 , где -3 ≤ x≤0
2) y=-(|x|-1)4 , где -3 ≤ x≤0
3) y=-(|x|-1)4 +8 , где -3 ≤ x≤0
3.

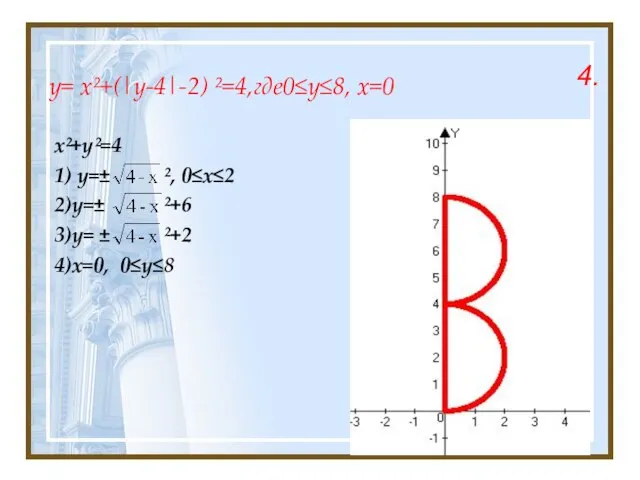
y= x²+(|y-4|-2) ²=4,где0≤y≤8, x=0
x²+y²=4
1) y=± ², 0≤x≤2
2)y=± ²+6
3)y= ± ²+2
4)x=0, 0≤y≤8
4.

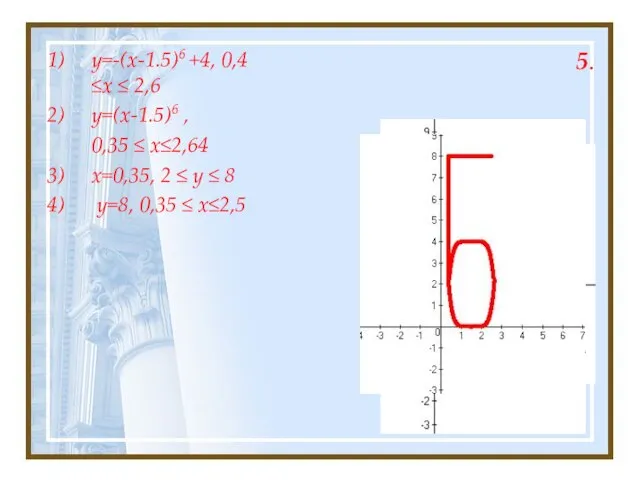
5.
y=-(x-1.5)6 +4, 0,4≤x ≤ 2,6
y=(x-1.5)6 ,
0,35 ≤ x≤2,64
x=0,35, 2 ≤ y ≤ 8
y=8, 0,35 ≤ x≤2,5

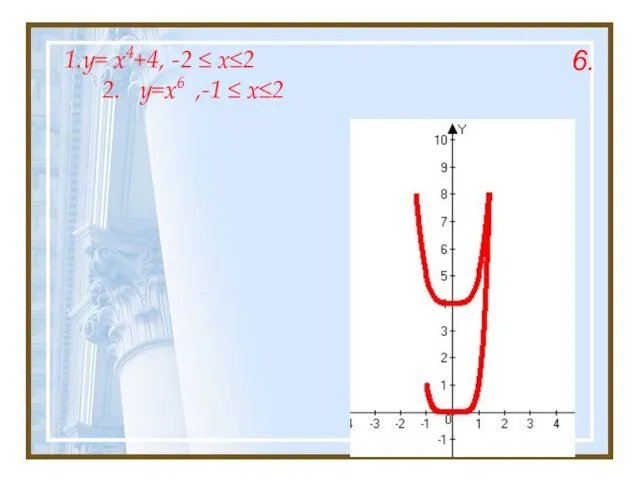
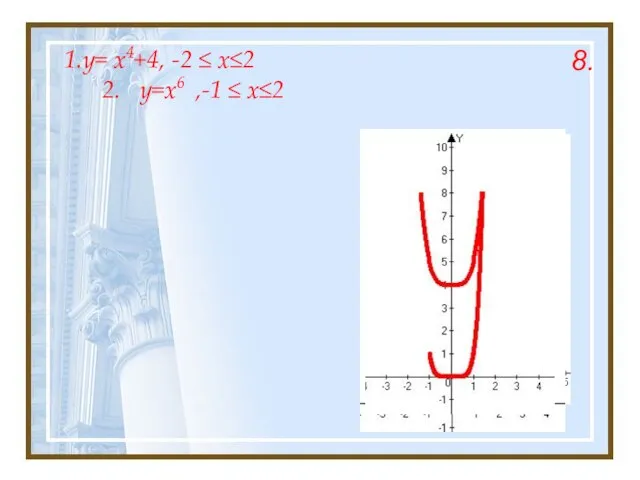
1.y= x4+4, -2 ≤ x≤2
2. y=x6 ,-1 ≤ x≤2
6.

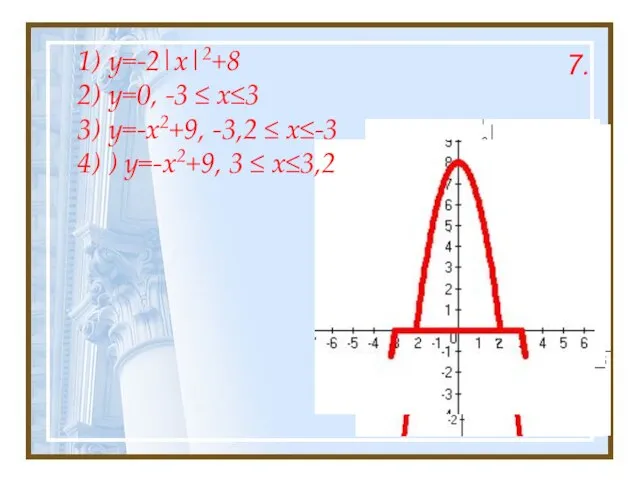
1) y=-2|x|2+8
2) y=0, -3 ≤ x≤3
3) y=-x2+9, -3,2 ≤ x≤-3
4) ) y=-x2+9, 3 ≤ x≤3,2
7.

1.y= x4+4, -2 ≤ x≤2
2. y=x6 ,-1 ≤ x≤2
8.

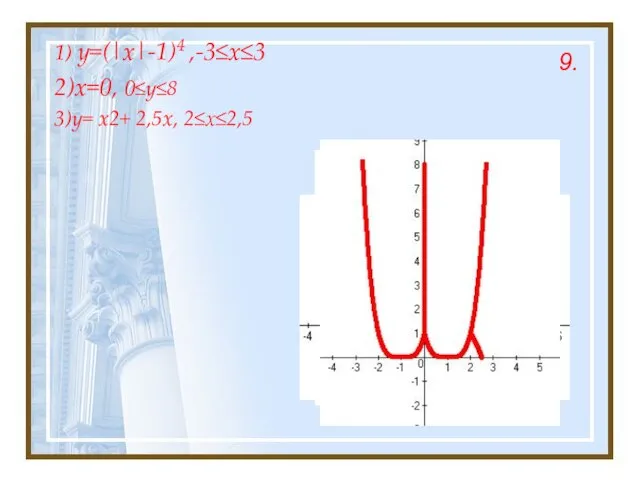
9.
1) y=(|x|-1)4 ,-3≤x≤3
2)x=0, 0≤y≤8
3)y= x2+ 2,5x, 2≤х≤2,5

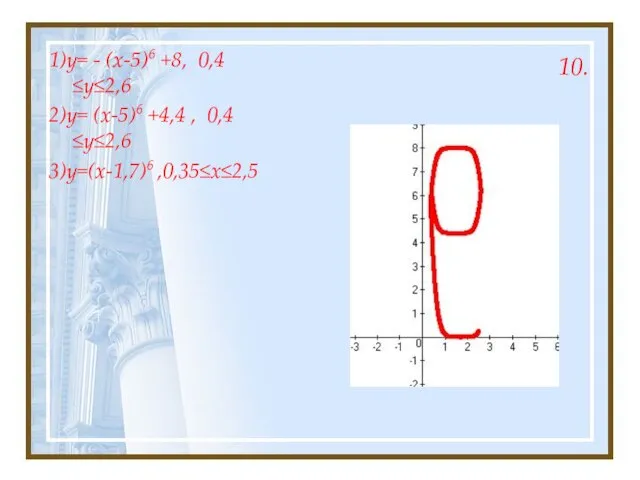
10.
1)y= - (x-5)6 +8, 0,4≤y≤2,6
2)y= (x-5)6 +4,4 , 0,4≤y≤2,6
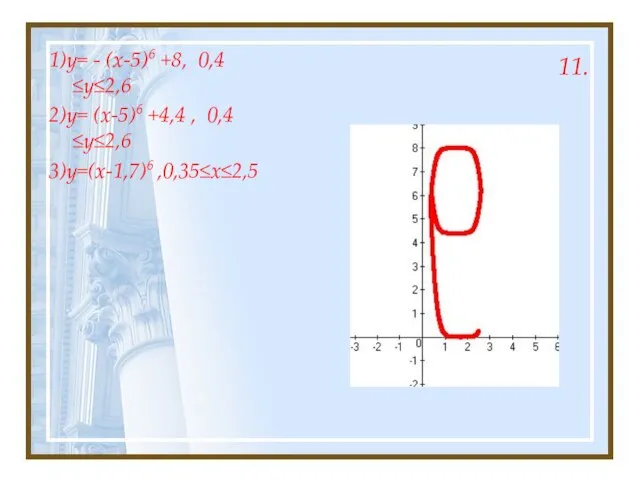
3)y=(x-1,7)6 ,0,35≤x≤2,5

11.
1)y= - (x-5)6 +8, 0,4≤y≤2,6
2)y= (x-5)6 +4,4 , 0,4≤y≤2,6
3)y=(x-1,7)6 ,0,35≤x≤2,5