Содержание
- 2. СОДЕРЖАНИЕ Симметрия в геометрических преобразованиях графиков функций Графики функций вида y=|f(x)|, y=f(|x|) График функции y=|f(|x|)| Графики
- 3. СИММЕТРИЯ СНЕЖИНКИ Я хочу сказать вам лично, Что снежинка –симметрична! И зеркальна, и центральна, А не
- 4. Симметрия в геометрических преобразованиях графиков функций Термин «симметрия» по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей».
- 5. Осевая Симметрия Преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно
- 6. Центральная симметрия Преобразование, переводящее каждую точку А фигуры (тела) в точку А ', симметричную ей относительно
- 7. Трансляционная симметрия Поворот Преобразование, при котором каждая точка А фигуры (тела) поворачивается на один и тот
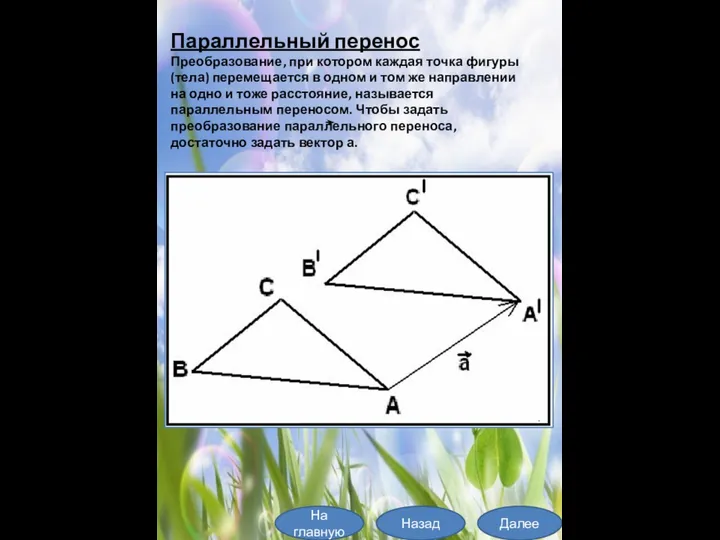
- 8. Параллельный перенос Преобразование, при котором каждая точка фигуры (тела) перемещается в одном и том же направлении
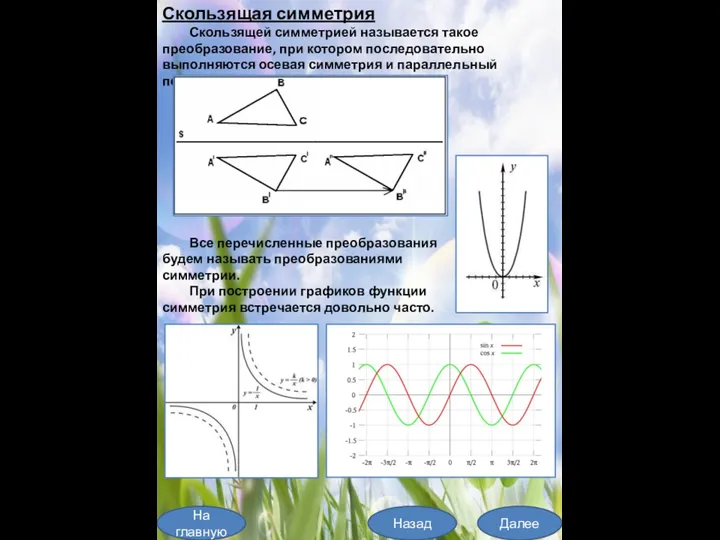
- 9. На главную Далее Назад Скользящая симметрия Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая
- 10. На главную Далее Назад Множество действительных чисел называется симметричным относительно точки х=0 числовой оси, если вместе
- 11. Графики функций вида y=|f(x)|, y=f(|x|) 1. Построение графика функции вида y=|f(x)| Чтобы построить график функции вида
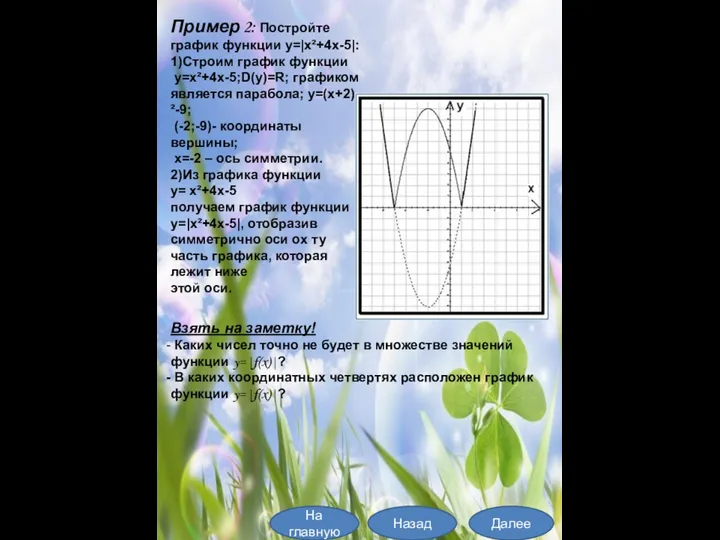
- 12. Пример 2: Постройте график функции y=|x²+4x-5|: 1)Строим график функции y=x²+4x-5;D(y)=R; графиком является парабола; y=(x+2)²-9; (-2;-9)- координаты
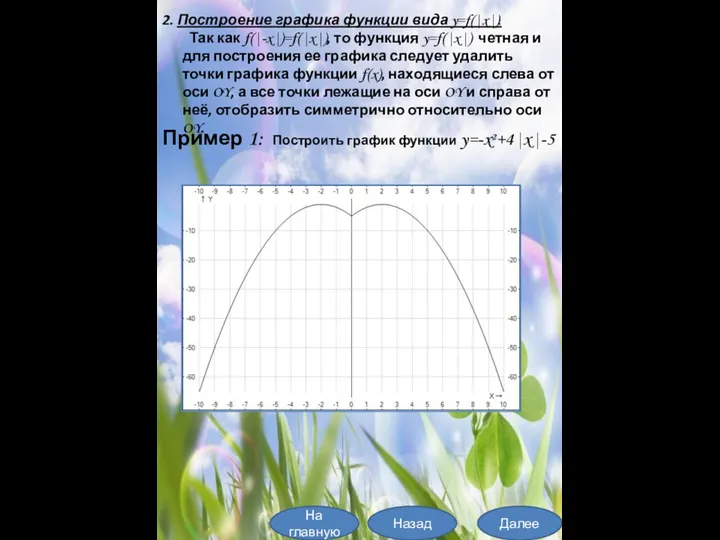
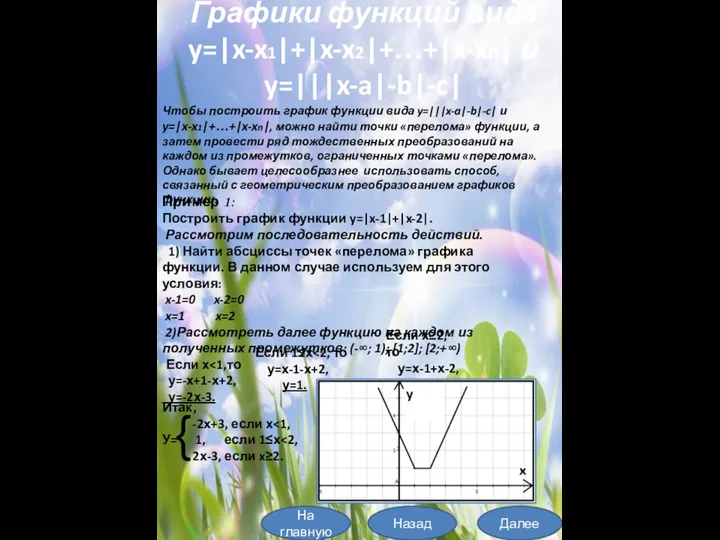
- 13. На главную Далее Назад Пример 1: Построить график функции y=-x²+4|x|-5 2. Построение графика функции вида y=f(|x|).
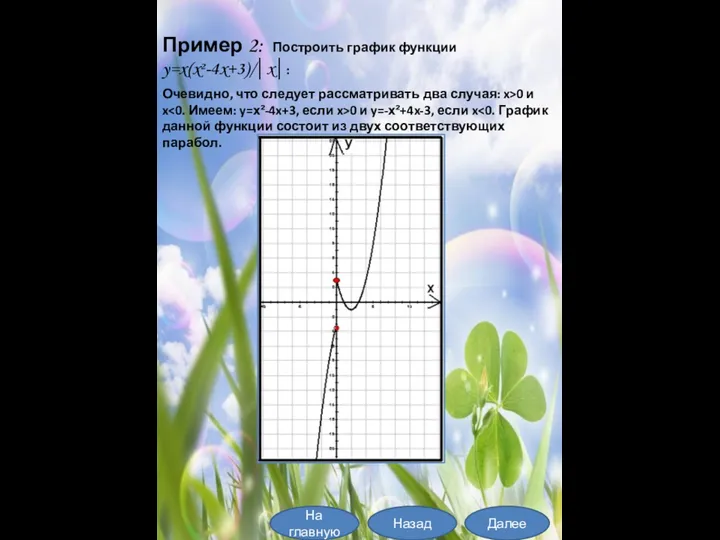
- 14. На главную Далее Назад Пример 2: Построить график функции y=x(x²-4x+3)/│x│: Очевидно, что следует рассматривать два случая:
- 15. График функции y=|f(|x|)| Чтобы построить график функции вида y=|f(|x|)| нужно: 1)Построить график функции y=f(x) для x≥0.
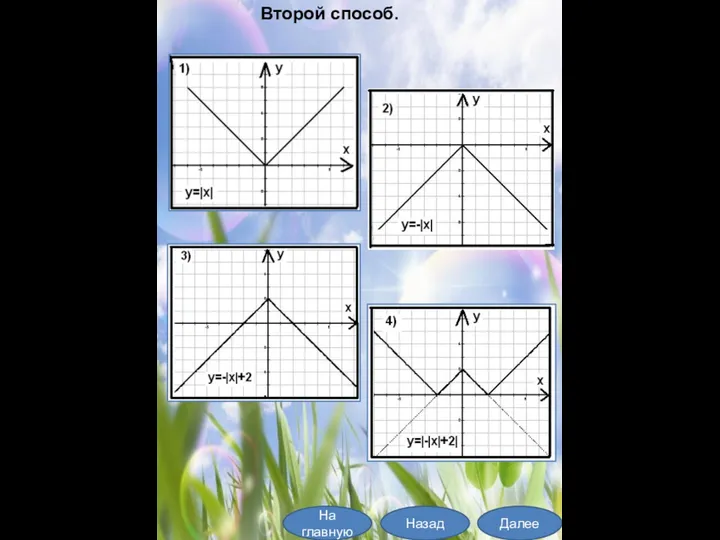
- 16. На главную Далее Назад Второй способ.
- 17. Графики «функций» |y|=f(x), при f(x)≥0; |y|=|f(x)| На главную Далее Назад 1. Построение графиков «функций» вида |y|=f(x)
- 18. 2.Построение графиков «функций» вида |y|=|f(x)|. Очевидно, что y=±|f(x)|, т.е. график «функции» будет симметричен относительно оси абсцисс.
- 19. Графики функций вида y=|x-x1|+|x-x2|+…+|x-xn| и y=|||x-a|-b|-c| На главную Далее Назад Чтобы построить график функции вида y=|||x-a|-b|-c|
- 20. Графический метод решения некоторых задач с параметрами На главную Далее Назад Пример1: Сколько корней имеет уравнение|x+3|=a?
- 21. На главную Далее Назад Пример 2. Найдите число решений уравнения |x²-2x-3|=a, в зависимости от параметра а.
- 22. На главную Далее Назад Пример 3: Решить уравнение x|x-4|+a=0. Решение: Строим график функции f(x) = -x|x-4|=
- 23. Построение графиков «функций», аналитические выражения которых содержат знак модуля, выраженных неявно На главную Далее Назад Пример
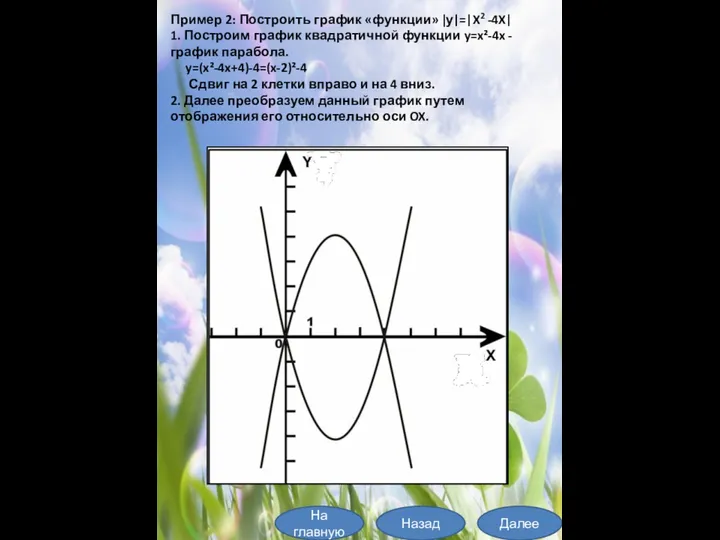
- 24. Пример 2: Построить график «функции» |y|=|X2 -4X| 1. Построим график квадратичной функции y=x²-4x - график парабола.
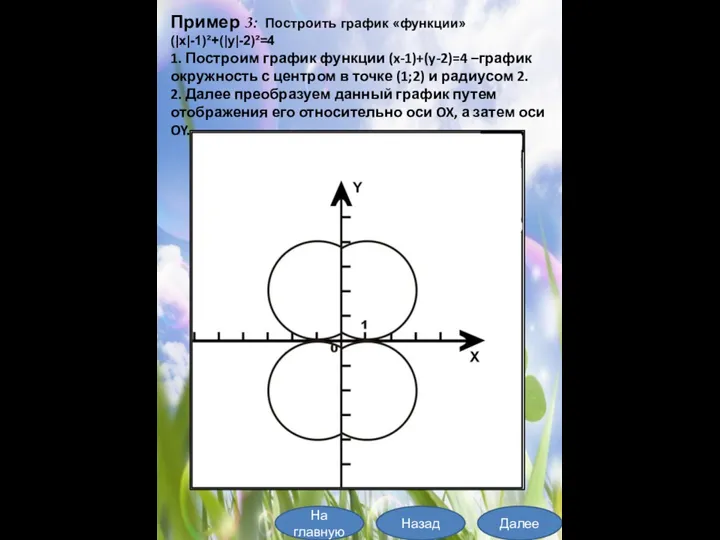
- 25. На главную Далее Назад Пример 3: Построить график «функции» (|x|-1)²+(|y|-2)²=4 1. Построим график функции (x-1)+(y-2)=4 –график
- 26. На главную Далее Назад Задание 1: Решить систему уравнений |x|+|y|=1 |x|+y=1 1. Решим систему уравнений с
- 27. На главную Далее Назад Задание 2: Решить систему уравнений |x-1|+|y-5|=1 y=5+|x-1| Задание 2: 1. Построим в
- 28. Построение множества точек плоскости, задаваемого соотношениями На главную Далее Назад Пример 1: Построить множество точек плоскости,
- 30. Скачать презентацию


















 Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Представляют геометрические фигуры
Представляют геометрические фигуры Матрицы. 1 часть
Матрицы. 1 часть Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Случаи сложения вида +5
Случаи сложения вида +5 Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Формирование алгоритмического мышления у младших школьников
Формирование алгоритмического мышления у младших школьников Формула Пика
Формула Пика Перпендикулярность плоскостей
Перпендикулярность плоскостей Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов
Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах
П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Математический марафон. Интеллектуальная игра
Математический марафон. Интеллектуальная игра Тригонометрия. Меры углов. Определения синуса, косинуса, тангенса, котангенса
Тригонометрия. Меры углов. Определения синуса, косинуса, тангенса, котангенса Задания с фигурами
Задания с фигурами Алгебра в жизни человека
Алгебра в жизни человека Презентация на тему Арифметическая прогрессия: практикум
Презентация на тему Арифметическая прогрессия: практикум 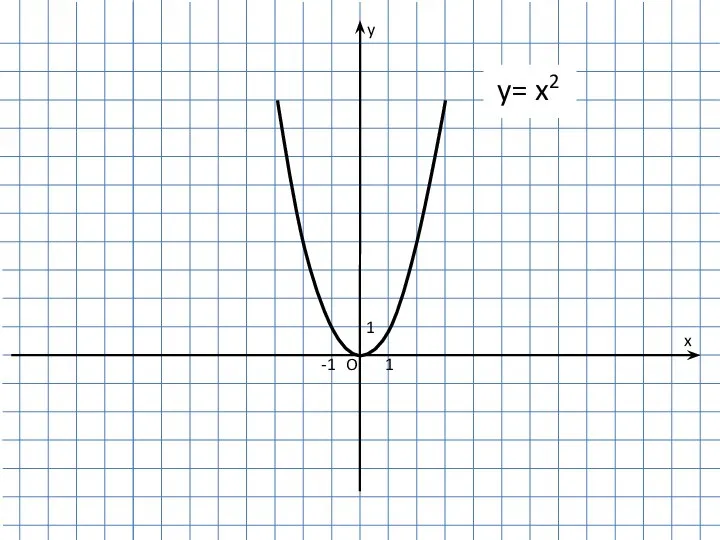 Функция y= x2
Функция y= x2 Семь чудес Кузбасса 5 класс
Семь чудес Кузбасса 5 класс Неравенство треугольника (7 класс)
Неравенство треугольника (7 класс) Формулы сокращенного умножения. Космический час на планете знаний
Формулы сокращенного умножения. Космический час на планете знаний Теория множеств
Теория множеств Многоугольники
Многоугольники Уравнение линии на плоскости
Уравнение линии на плоскости Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ
Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ  Прибавить и вычесть число 1
Прибавить и вычесть число 1 Площади и объемы многогранников. Решение задач
Площади и объемы многогранников. Решение задач