Содержание
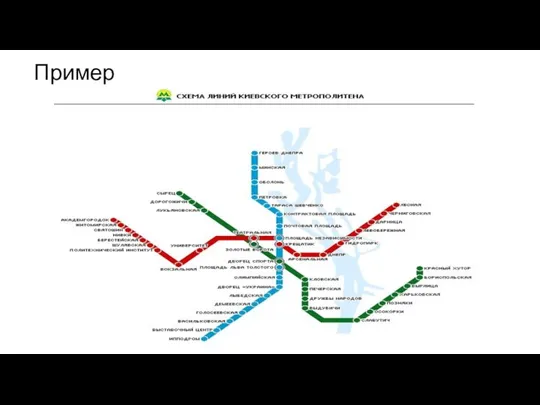
- 2. Пример
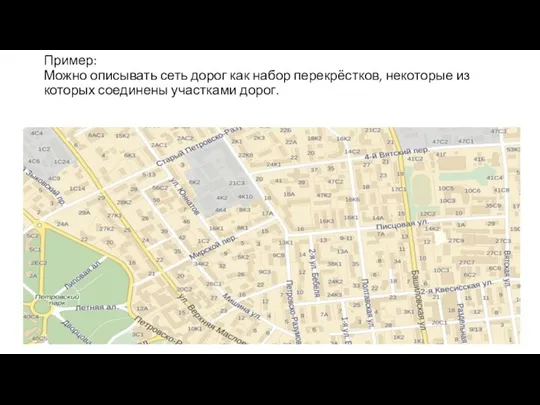
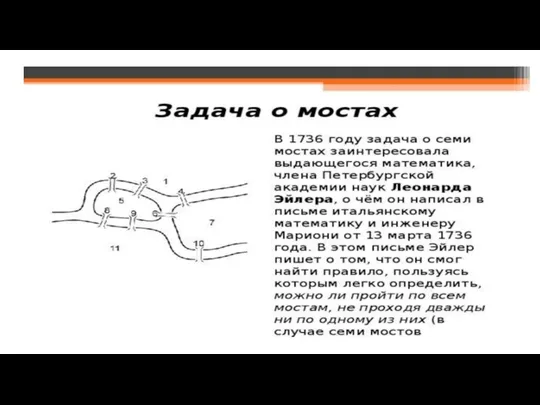
- 3. Пример: Можно описывать сеть дорог как набор перекрёстков, некоторые из которых соединены участками дорог.
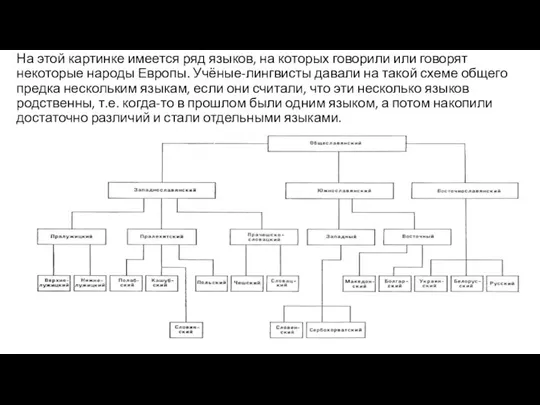
- 4. На этой картинке имеется ряд языков, на которых говорили или говорят некоторые народы Европы. Учёные-лингвисты давали
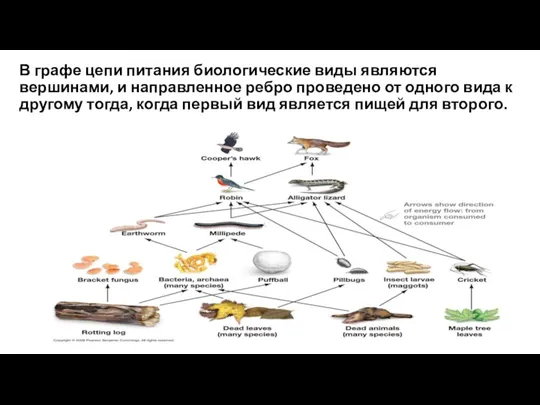
- 5. В графе цепи питания биологические виды являются вершинами, и направленное ребро проведено от одного вида к
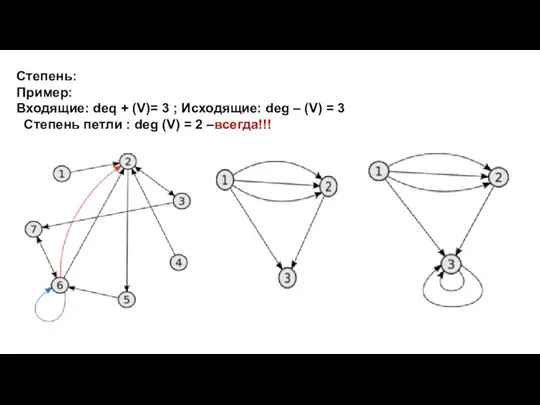
- 9. Степень: Пример: Входящие: deq + (V)= 3 ; Исходящие: deg – (V) = 3 Степень петли
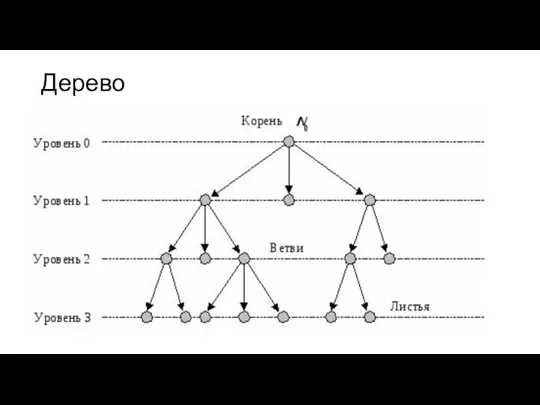
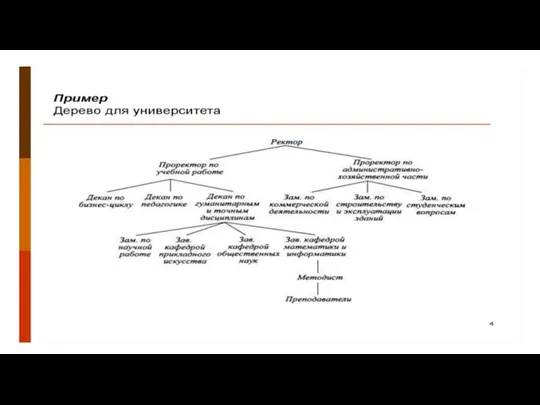
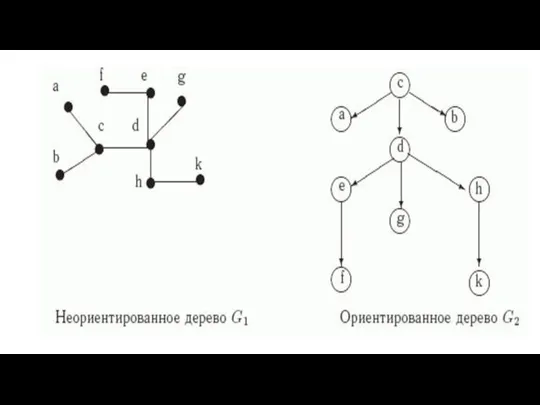
- 10. Дерево
- 11. Дерево
- 14. Задачи
- 15. Задача № 3 В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый
- 16. Задача 3. У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и
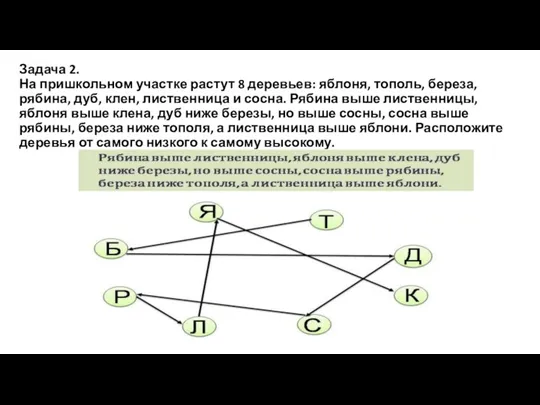
- 17. Задача 2. На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и
- 18. Задача №5. В первенстве класса по настольному теннису 6 участников: Андрей, Борис Виктор, Галина, Дмитрий и
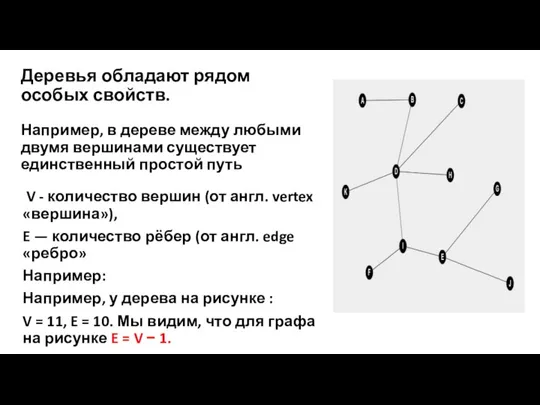
- 19. Деревья обладают рядом особых свойств. Например, в дереве между любыми двумя вершинами существует единственный простой путь
- 21. Задача 2 Сколько различных обедов П.И. Чичиков мог насчитать из блюд, выставленных на столе у П.П.
- 23. Скачать презентацию








 Объёмные тела в повседневной жизни
Объёмные тела в повседневной жизни Построение графиков в MathCAD
Построение графиков в MathCAD Построение треугольника
Построение треугольника Возведение в степень
Возведение в степень Диаграммы и графики. 6 класс
Диаграммы и графики. 6 класс Пересечение поверхностей
Пересечение поверхностей Тетраэдр
Тетраэдр Анализ уравнения на соответствие графику
Анализ уравнения на соответствие графику Презентация на тему Лобачевский Николай Иванович
Презентация на тему Лобачевский Николай Иванович  Урок математики с элементами театрализации
Урок математики с элементами театрализации Числовой коэффициент
Числовой коэффициент Понятие числовой окружности. Радианное измерение углов
Понятие числовой окружности. Радианное измерение углов Презентация на тему Сложение и вычитание натуральных чисел (5 класс)
Презентация на тему Сложение и вычитание натуральных чисел (5 класс)  Осевая симметрия
Осевая симметрия Задания по математике из учебника
Задания по математике из учебника Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Графы и их применение в архитектуре
Графы и их применение в архитектуре Скользящее среднее
Скользящее среднее Интегральное исчисление. Первообразная функция. Неопределённый интеграл. Методы интегрирования. Определенный интеграл
Интегральное исчисление. Первообразная функция. Неопределённый интеграл. Методы интегрирования. Определенный интеграл Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА
Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА  Тригонометрические уравнения
Тригонометрические уравнения Параллельный перенос
Параллельный перенос Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Зачёт по таблице умножения
Зачёт по таблице умножения Простейшие вероятностные задачи
Простейшие вероятностные задачи Построение графика функции заданной параметрически
Построение графика функции заданной параметрически Подобие. Коэффициент подобия
Подобие. Коэффициент подобия Предельные величины, эластичности
Предельные величины, эластичности