Содержание
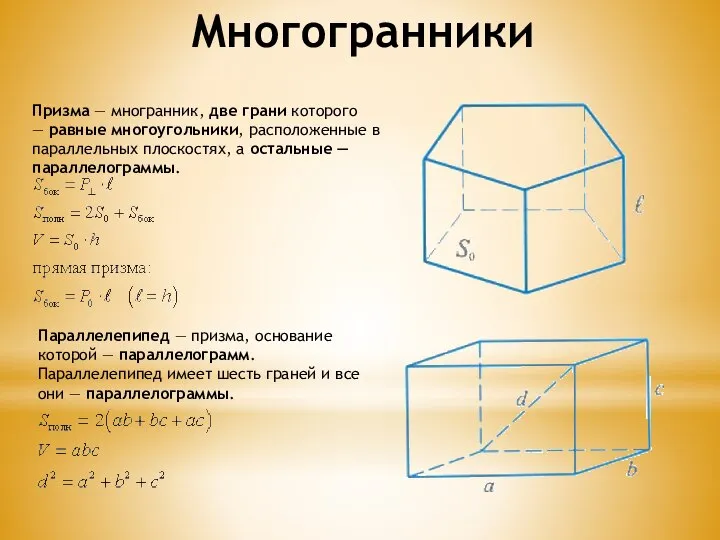
- 2. Призма — многранник, две грани которого — равные многоугольники, расположенные в параллельных плоскостях, а остальные —
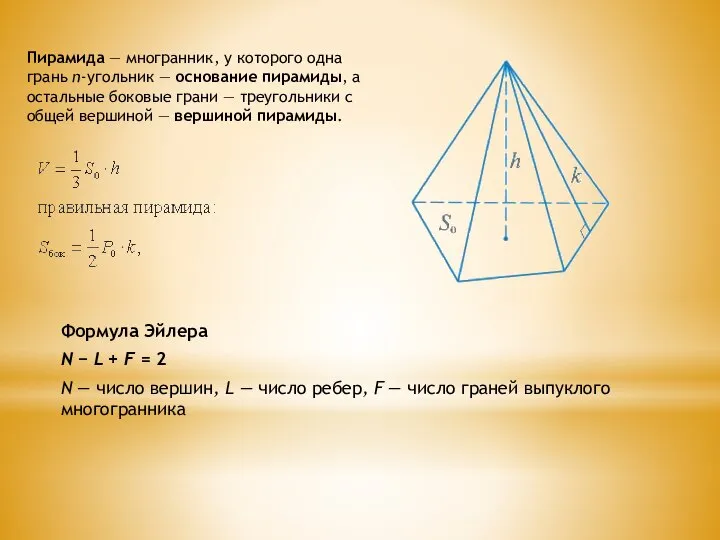
- 3. Пирамида — многранник, у которого одна грань n-угольник — основание пирамиды, а остальные боковые грани —
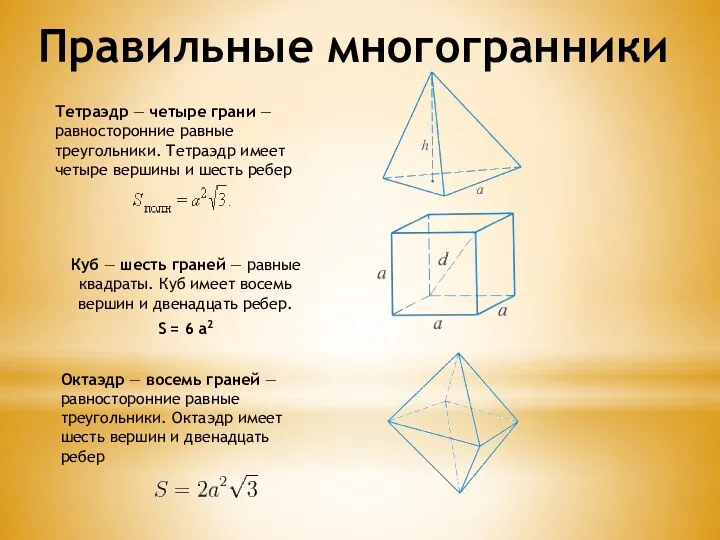
- 4. Тетраэдр — четыре грани — равносторонние равные треугольники. Тетраэдр имеет четыре вершины и шесть ребер Куб
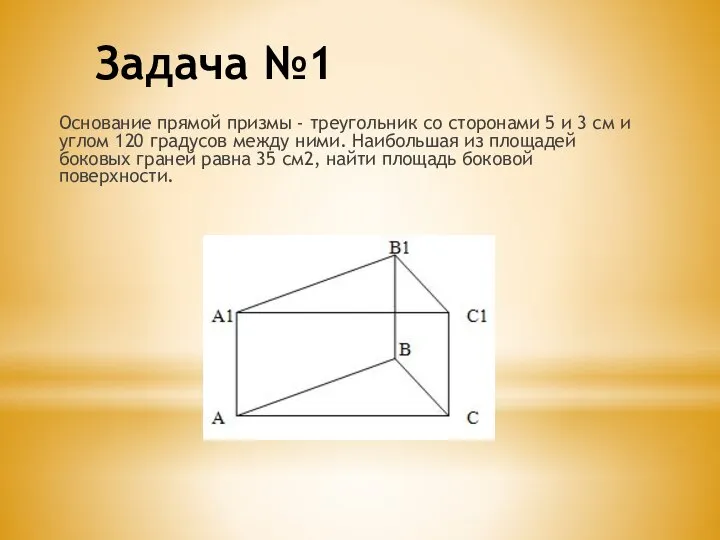
- 7. Задача №1 Основание прямой призмы - треугольник со сторонами 5 и 3 см и углом 120
- 8. Решение. Согласно теореме косинусов Откуда AC2 = AB2 + BC2 - 2*AB*BC*cos 120 AC2 = 25
- 9. Задача №2 Условие Дана пирамида АВСD (см. рис.). Известно, что ADB = DBC; ABD = BDC;
- 10. Решение Используя признаки равенства треугольников, докажем, что все грани пирамиды - равные треугольники. ADB = CBD
- 12. Скачать презентацию




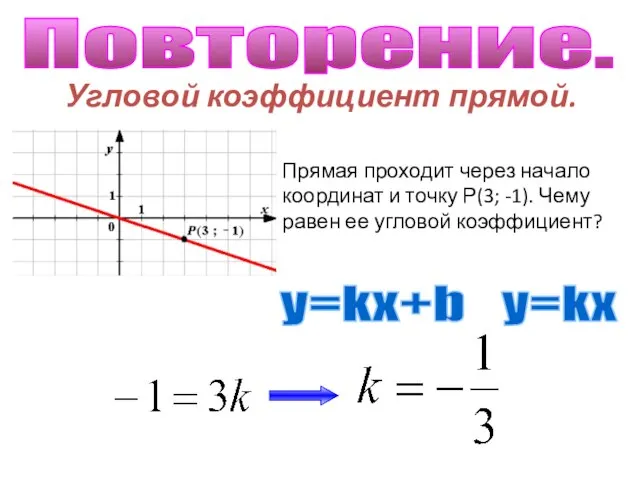 Угловой коэффициент прямой.
Угловой коэффициент прямой. Презентация на тему Десятичные дроби (6 класс)
Презентация на тему Десятичные дроби (6 класс)  Теорема Пифагора
Теорема Пифагора Градусная мера дуги окружности. Теорема о вписанном угле
Градусная мера дуги окружности. Теорема о вписанном угле Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Презентация на тему Приведение дробей к общему знаменателю
Презентация на тему Приведение дробей к общему знаменателю  Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Основы теории статистических показателей
Основы теории статистических показателей Метод ортогональных исключений. Ортогональные отражения
Метод ортогональных исключений. Ортогональные отражения Основная тенденция развития РД
Основная тенденция развития РД Центральные и вписанные углы
Центральные и вписанные углы Графики тригонометрических функций. Преобразование графиков
Графики тригонометрических функций. Преобразование графиков Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление Презентация на тему Небесная геометрия
Презентация на тему Небесная геометрия  Умножение натуральных чисел
Умножение натуральных чисел Презентация на тему Умножение многочлена на многочлен
Презентация на тему Умножение многочлена на многочлен  Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Элементы комбинаторики АТ
Элементы комбинаторики АТ Презентация на тему Подготовка к контрольной работе по алгебре
Презентация на тему Подготовка к контрольной работе по алгебре  Баскетбол. Математическая викторина
Баскетбол. Математическая викторина Парная регрессия: линейный анализ
Парная регрессия: линейный анализ Математическая статистика
Математическая статистика Решение текстовых задач на ЕГЭ
Решение текстовых задач на ЕГЭ Последовательность процентных расчетов при осуществлении банковских операций
Последовательность процентных расчетов при осуществлении банковских операций Один и много
Один и много Подготовка к контрольной работе
Подготовка к контрольной работе Стереометрия. Тренажер
Стереометрия. Тренажер Параллельные плоскости
Параллельные плоскости