Содержание
- 2. Что такое числовая последовательность? Какие бывают виды числовых последовательностей? Как задаётся числовая последовательность? Что такое предел
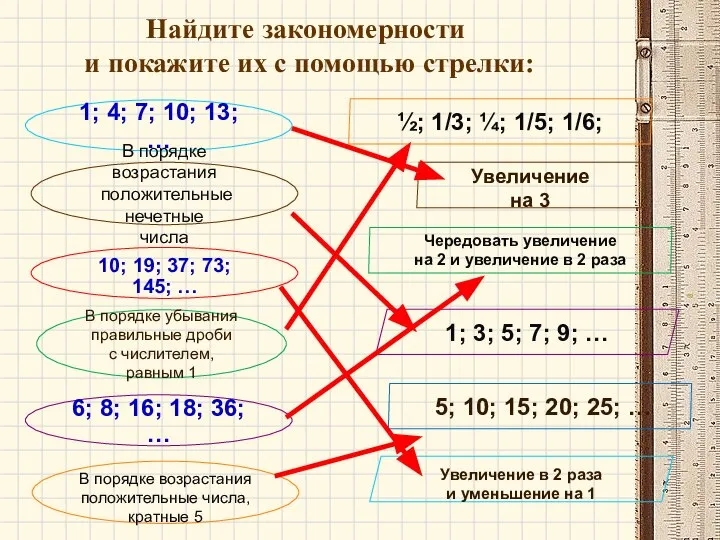
- 3. Найдите закономерности и покажите их с помощью стрелки: 1; 4; 7; 10; 13; … В порядке
- 4. Что такое числовая последовательность? Если каждому натуральному числу п поставлено в соответствие некоторое действительное число хп
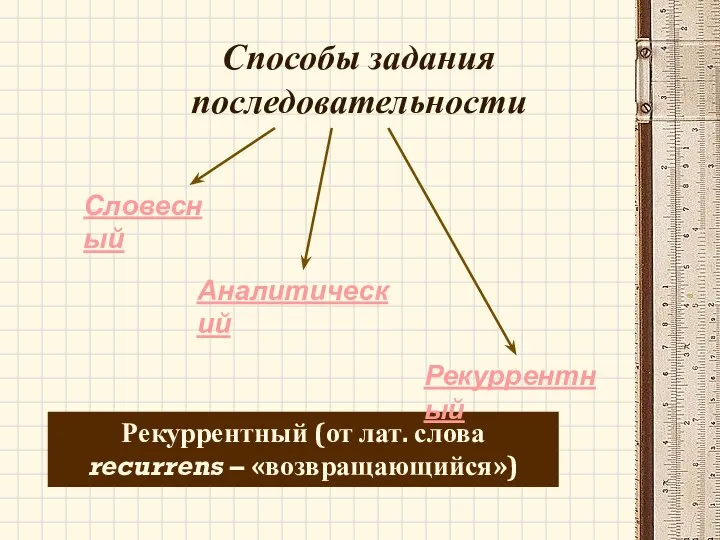
- 5. Способы задания последовательности Рекуррентный (от лат. слова recurrens – «возвращающийся») Аналитический Словесный Рекуррентный
- 6. Словесный способ. Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности
- 7. Аналитический способ. с помощью формулы. Пример 1. Последовательность чётных чисел: y = 2n; 2, 4, 6,
- 8. Рекуррентный способ. Указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы. Пример 1.
- 9. Предел числовой последовательности Рассмотрим две числовые последовательности: : 2, 4, 6, 8, 10, …, 2п ,…;
- 10. Замечаем, что члены последовательности уп как бы «сгущаются» около точки 0, а у последовательности хп таковой
- 11. Определение: Пусть a - точка прямой, а r -положительное число. Интервал (a-r, a+r) называют окрестностью точки
- 12. Теперь можно перейти к определению точки «сгущения», которую математики назвали «пределом последовательности». Например (-0.1, 0.5) –
- 13. Число b называется пределом последовательности {уп } если в любой заранее выбранной окрестности точки b содержатся
- 14. Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
- 15. Рассмотрим последовательность: – гармонический ряд Если │q│ Если │q│> 1, то последовательность уn = q n
- 16. Свойства пределов предел частного равен частному пределов: предел произведения равен произведению пределов: предел суммы равен сумме
- 17. Примеры:
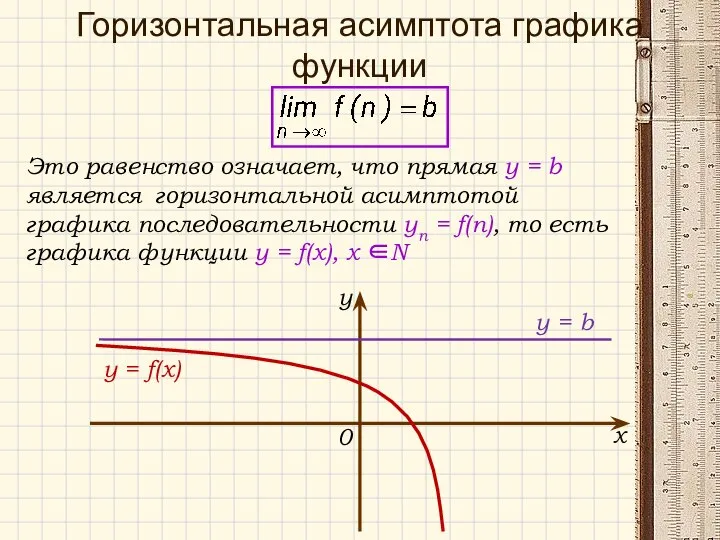
- 18. Это равенство означает, что прямая у = b является горизонтальной асимптотой графика последовательности yn = f(n),
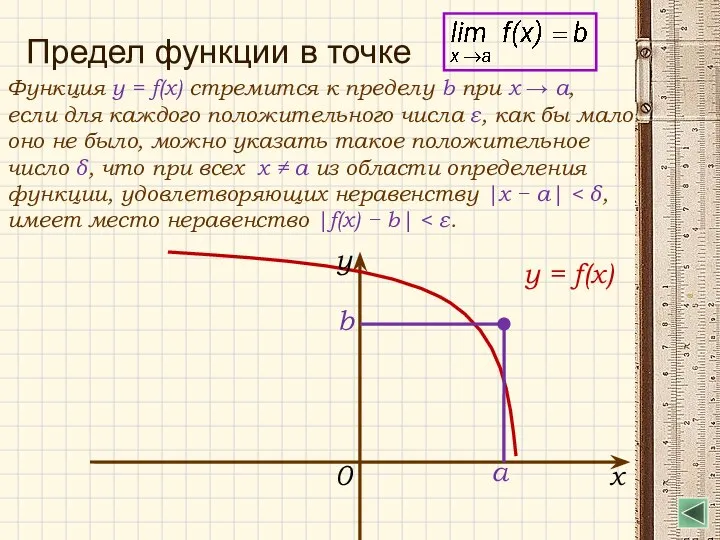
- 19. Предел функции в точке Функция y = f(x) стремится к пределу b при x → a,
- 20. Непрерывность функции в точке Функцию y = f(x) называют непрерывной в точке x = a, если
- 21. Понятие непрерывности функции На рисунке изображен график функции, состоящий из двух «кусков». Каждый из них может
- 26. Скачать презентацию
















 Презентация на тему Виды движения
Презентация на тему Виды движения  Куб
Куб urok TViMS NSV
urok TViMS NSV Решение задания С-2 ЕГЭ
Решение задания С-2 ЕГЭ Интерактивный тренажёр Повторяем величины с домовёнком
Интерактивный тренажёр Повторяем величины с домовёнком preobrazovanie
preobrazovanie Решение дифференциальных уравнений первого порядка
Решение дифференциальных уравнений первого порядка Презентация на тему Прямоугольник
Презентация на тему Прямоугольник  Уравнение сферы
Уравнение сферы Решение задач (1 класс)
Решение задач (1 класс) Устный счёт
Устный счёт Числа-гиганты. Из истории чисел - гигантов
Числа-гиганты. Из истории чисел - гигантов Неполные квадратные уравнения
Неполные квадратные уравнения Презентация на тему Решение задач на нахождение неизвестного по двум разностям
Презентация на тему Решение задач на нахождение неизвестного по двум разностям  Окружность. 5 класс
Окружность. 5 класс Фрактал
Фрактал Кратные числа
Кратные числа Действия с десятичными дробями
Действия с десятичными дробями Период математического маятника
Период математического маятника Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Формулы сложения. Тригонометрические формулы
Формулы сложения. Тригонометрические формулы Методы решения систем уравнения
Методы решения систем уравнения Доказательство равносильностей
Доказательство равносильностей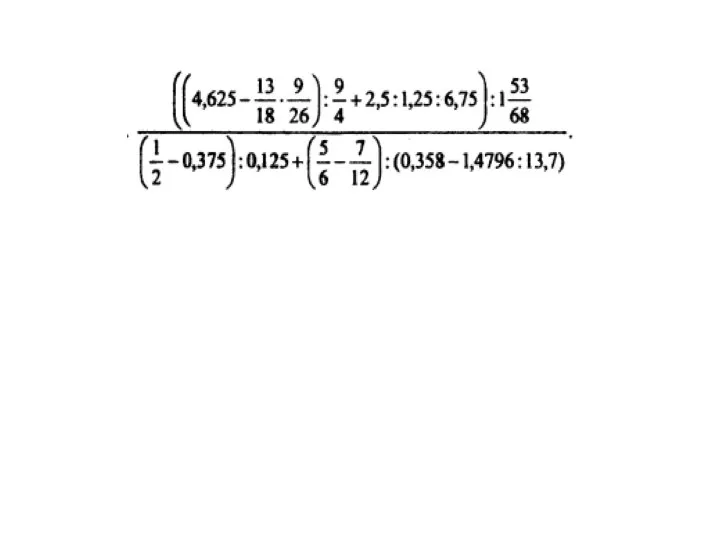 Тождественное преобразование алгебраических выражений. Продолжение
Тождественное преобразование алгебраических выражений. Продолжение Теорема об интегрировании рядов Фурье
Теорема об интегрировании рядов Фурье Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся
Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся Домашняя самостоятельная работа
Домашняя самостоятельная работа По следам теоремы Пифагора
По следам теоремы Пифагора