Содержание
- 2. Цель урока: Ввести определение степени с целым отрицательным показателем. Повторить свойства степени с натуральным показателем, нахождение
- 3. А. x>2 Б. x I. Актуализация знаний учащихся (фронтальная работа с классом) 1.Найти область определения функции
- 4. А. 1) и 3) Б. 1) и 2) В. 3) и 4) Г. 1) и 4)
- 5. 5. Найти область значения функции: В. [0;9]; 6. Возведите в степень: 4
- 6. II. Изучение нового материала: n раз Если , то Если - любое число, то т.е. 5
- 7. Свойства степени с натуральным показателем: а и b – любые числа 6
- 8. Выражение целесообразно считать числом, обратным степени того же основания с противоположным показателем, т.е. дробью Рассмотрим выражение:
- 9. Пример 1 Вычислить 1) 2) 3) 4) 8
- 10. Пример 2 Доказать, что Вывод: При умножении степеней с одинаковыми основаниями показатели складываются. При делении степеней
- 11. При возведении степени в степень показатели перемножаются. Свойства степени с натуральными показателями сохраняются и для отрицательных
- 12. Закрепление изученного материала Представить выражение в виде степени, используя определение: 11
- 13. Записать выражение в виде степени Найдите ошибку: 1. 2. 3. 4. 5. 12
- 14. Самостоятельная работа Вариант 1 Вариант 2 13
- 15. Применение понятия степени с целым показателем. Для вычислений используют числа в стандартном виде. Число =274,35 можно
- 16. Число =0,0013 можно записать так: Число, стоящее перед запятой, однозначное, умноженное на 10 в целой степени.
- 17. Укажите число, равное 0,00056 А. Б. В. Г. Представьте число в стандартном виде: 1) 1800000 А.
- 18. Пример: вычислить Найти значение выражения А. 6400 Б. 0,064 В. 0,0064 Г. 0,00064 17
- 19. Для биологической лаборатории купили оптический микроскоп, который дает возможность различать объекты размером до Выразите эту величину
- 20. Готовимся к итоговой аттестации Часть А. Вычислите: а) 1) 9 2) -9 3) 17 4) б)
- 21. Найти область существования выражения: 20
- 22. Сколько целых чисел содержит промежуток А. 5 Б. 4 В. 3 Г. 2 21
- 23. Представьте выражение в виде степени с целым показателем: А. Б. В. х Г. 22
- 25. Скачать презентацию



![5. Найти область значения функции: В. [0;9]; 6. Возведите в степень: 4](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/286074/slide-4.jpg)


















 Презентация на тему Биссектриса угла в треугольнике
Презентация на тему Биссектриса угла в треугольнике  Вопросы при решении задач
Вопросы при решении задач Вычислить. Задание на лето
Вычислить. Задание на лето Правильные многогранник. Повторение
Правильные многогранник. Повторение Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Понятия равно, не равно
Понятия равно, не равно Численные методы механики сплошных сред. Индивидуальные задания
Численные методы механики сплошных сред. Индивидуальные задания Решение типовой задачи
Решение типовой задачи Звездчатые многогранники
Звездчатые многогранники Законы алгебры логики. Задания
Законы алгебры логики. Задания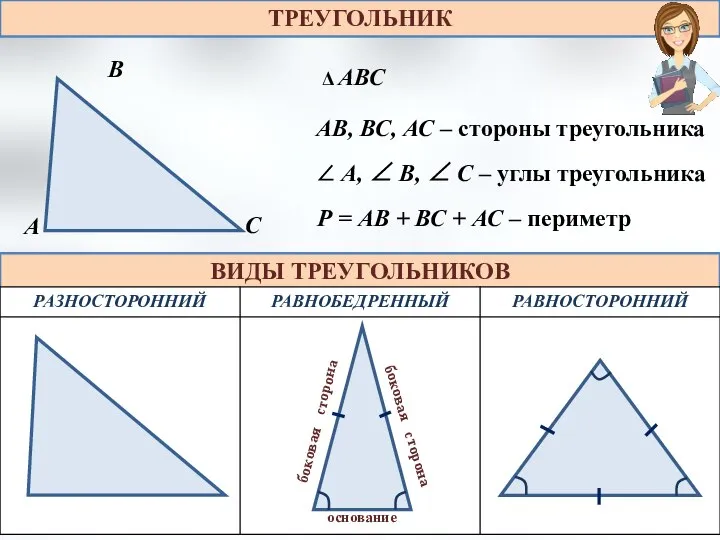 Треугольник
Треугольник Применение производной для исследования функций на монотонность
Применение производной для исследования функций на монотонность Розвязування задач
Розвязування задач Математическое моделирование. Рандомизация
Математическое моделирование. Рандомизация Презентация4. МСиТИ
Презентация4. МСиТИ Решение задач
Решение задач Официальная статистика как условие устойчивого развития сельского хозяйства
Официальная статистика как условие устойчивого развития сельского хозяйства Теория множеств
Теория множеств Соотношение между гипотенузой и катетами прямоугольного треугольника
Соотношение между гипотенузой и катетами прямоугольного треугольника Состав чисел в пределах 10. Закрепление пройденного
Состав чисел в пределах 10. Закрепление пройденного Геометрия в жизни человека
Геометрия в жизни человека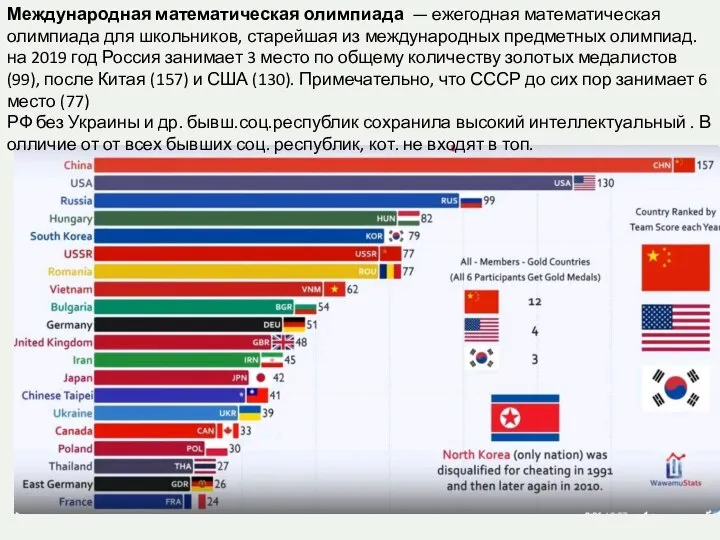 Международная математическая олимпиада
Международная математическая олимпиада Поворот. Типы вращений
Поворот. Типы вращений Объем конуса
Объем конуса Компьютерный и интеллектуальный анализ данных. Теория вероятностей
Компьютерный и интеллектуальный анализ данных. Теория вероятностей Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Решение дробных рациональных уравнений. Алгебра 8 класс
Решение дробных рациональных уравнений. Алгебра 8 класс