Случайные сигналы и их математические модели

Случайные сигналы и их математические модели
Случайные процессы и их математические характеристики
На практике все сигналы, которые предназначены для передачи информации, носят случайный характер. Именно в случайности изменения сигналов заложена информация, которую необходимо передать получателю.
Помимо этого, при передаче сигналов действуют помехи, которые также носят случайный характер.
В отличие от детерминированных сигналов значения случайного сигнала в некоторый момент времени невозможно предсказать точно. Вместе с тем, описание таких сигналов возможно в вероятностном смысле через усредненные (статистические) характеристики.

Математическими моделями случайных сигналов и помех являются случайные процессы.
Случайным процессом называется изменение случайной величины во времени.
К случайным процессам относится большинство процессов, протекающих в радиотехнических устройствах, а также помехи, сопровождающие передачу сигналов по каналам связи.
Случайные процессы могут быть непрерывными, либо дискретными в зависимости от того, какая случайная величина непрерывная или дискретная, изменяется во времени.

В теории вероятностей основным понятием является случайное событие, которое при проведении эксперимента может произойти, а может и не произойти.
Если, например, проводится эксперимент, включающий серию из n испытаний радиотехнического устройства, то результатом каждого испытания может быть либо рабочее состояние устройства, либо его отказ, которые представляют собой события. Но при каждом конкретном испытании отказ может произойти, а может и не произойти. В этом смысле отказ является случайным событием.
Обозначим случайное событие буквой А. Центральным в теории вероятностей является определение частоты наступления события А.
где
- число испытаний, соответствующих наступлению события А
- общее число испытаний

При достаточно большом числе всех проведенных испытаний (теоретически при n→∞) частота наступления события А отождествляется с вероятностью
Отсюда следует, что 0 ≤ р(А) ≤ 1 - т.е. вероятность является неотрицательной величиной, принимающей значение в диапазоне чисел от 0 до 1.
Если р(А)=0 то событие называется невозможным, если р(А)=1 то событие называется достоверным.
Понятие вероятности можно применить и к группе событий А1, А2, …,Аi…, Аn.
Если
то события образуют полную группу и в результате испытания одно из них наступит обязательно.
События называются несовместными, если появление одного из них исключает появление другого.

Если в результате эксперимента возможно одновременное наступление событий, они называются совместными.
Пример: радиоприемник исправен (событие А) и настроен на заданную частоту (событие В).
Вероятность наступления события В при условии, что произошло событие А, называется условной вероятностью р(В/А).
Вероятность одновременного наступления совместных событий А и В определяется выражением
События А и В называются независимыми, если наступление одного из них не связано с наступлением другого. Вероятность наступления двух независимых совместных событий равна
Отсюда следует, что для независимых совместных событий условная вероятность р(В/А)=р(В), т.е. равна безусловной вероятности.

Вероятность события А , которое может наступить с одним из событий Н1, Н2, …,Нj…, НN, образующих полную группу несовместных событий, называемых гипотезами, определяется формулой полной вероятности
Вероятность наступления гипотезы Нj, после того, как наступило событие А, определяется формулой Байеса
Случайные события характеризуют эксперимент с качественной стороны.
На практике, как правило, требуется количественная оценка результата. Если в результате эксперимента наступает или не наступает событие А, этому случайному событию можно поставить в соответствие величину, принимающую только два значения: 1 или 0 в зависимости от того, произошло событие или нет.
Так как событие А случайно, случайной будет и величина, оценивающая результат эксперимента.

Обозначим случайную величину через Х, а значения, которые она может принимать,− через х. Если случайная величина (СВ) Х принимает значения из множества
возможных конкретных значений, то такая СВ называется дискретной СВ.
Если же множество значений Х непрерывно, то такая величина называется непрерывной СВ.
Как дискретная, так и непрерывная СВ полностью характеризуются законами распределения.
Функцией распределения дискретной СВ называется зависимость
Функция распределения непрерывной СВ представляет собой зависимость
и является интегральным законом распределения непрерывной СВ

Плотностью распределения непрерывной СВ называется зависимость
представляет собой отношение вероятности р(Δх) того, что непрерывная СВ будет находиться в пределах элементарного интервала Δх к величине этого интервала.
Если функция F(x) непрерывна, и интервал значений СВ составляет (- ∞ ≤ х ≤ ∞), то функция распределения и плотность распределения связаны между собой соотношениями

Понятия законов распределения можно распространить и на совокупность случайных величин. Так, для двух случайных величин функцией распределения называется вероятность того, что случайная величина не превзойдет значения
Очевидно, что данная функция является двумерной.
Двумерная плотность распределения двух СВ
Если случайные величины Х и Y независимы, то
При наличии зависимости случайных величин

2. Числовые характеристики случайных процессов
− вероятность попадания дискретной СВ в интервал (a,b) равна
- вероятность попадания непрерывной СВ в интервал (a,b) равна
- математическое ожидание дискретной СВ
- математическое ожидание непрерывной СВ
- математическое ожидание случайного процесса

- дисперсия дискретной СВ
- дисперсия непрерывной СВ
Для зависимых случайных величин имеет место функция корреляции
характеризующая степень зависимости этих величин.
- дисперсия случайного процесса
Важнейшей характеристикой случайного процесса служит автокорреляционная функция (АКФ)
устанавливающая степень статистической связи между значениями СП в моменты времени t1 и t2

Взаимную связь между двумя случайными процессами устанавливает взаимная корреляционная функция (ВКФ).
Взаимная корреляционная функция характеризует степень статистической связи между значениями случайных процессов в моменты времени t и t+τ
Часто используют коэффициент взаимной корреляции
Если ρ=0, то случайные процессы некоррелированны (независимы).

Представление СП в виде ансамбля реализаций приводит к понятию стационарности процесса. Случайный процесс является стационарным, если все начальные и центральные моменты не зависят от времени, т.е.
Это жесткие условия, поэтому при их выполнении СП считается стационаром в узком смысле
На практике используется понятие стационарности в широком смысле. Случайный процесс стационарен в широком смысле, если его математическое ожидание и дисперсия не зависят от времени, т.е.:
а автокорреляционная функция определяется только интервалом τ=t2-t1 и не зависит от выбора t1

Случайный процесс называется эргодическим, если его вероятностные характеристики, полученные усреднением по ансамблю, совпадают с вероятностными характеристиками, полученными усреднением по времени единственной реализации из этого ансамбля.
- математическое ожидание – это среднее значение (постоянная составляющая) процесса.
- дисперсия, имеет физический смысл средней мощности переменной составляющей процесса
- автокорреляционная функция

Использование выражений для нахождения характеристик эргодического СП требует реализации случайного процесса большой (теоретически бесконечной) протяженности.
При решении практических задач интервал времени Т ограничен. При этом большинство процессов считают приблизительно эргодическими и вероятностные характеристики определяют в соответствии с выражениями
Случайные процессы, у которых исключено математическое ожидание, называются центрированными.

В практической радиотехнике наиболее широко используются следующие законы распределения, которые обычно описываются рядом распределения для дискретных СВ и плотностью вероятности – для непрерывных СВ.
Для дискретных СВ
− равномерный закон:
- биномиальный закон определяет вероятность числа k появления случайного события при n независимых испытаниях (например, вероятность появления k единиц в кодовой комбинации из n разрядов):
3. Законы распределения случайных величин

Для непрерывных СВ
− равномерный закон
где (a, b) – область определения случайной величины;
- нормальный закон
- закон Релея - определяет распределения модуля вектора на плоскости, составляющие которого по обеим осям независимы и распределены нормально с нулевым математическим ожиданием и дисперсией σ2.

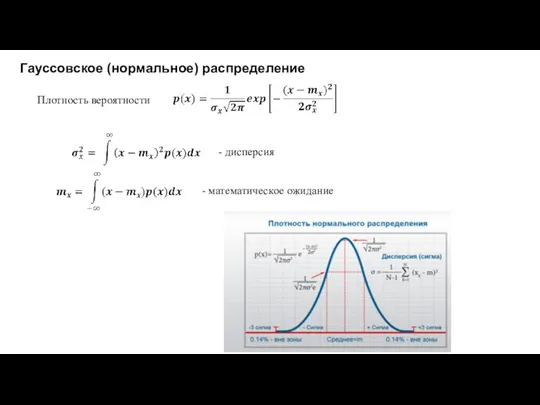
Плотность вероятности
- дисперсия
- математическое ожидание
Гауссовское (нормальное) распределение

4. Энергетический спектр случайного процесса
Передача информации в радиотехнических системах связана со спектральными преобразованиями сигналов.
Спектры детерминированных сигналов определяются преобразованием Фурье
где s(t) – детерминированная функция, описывающая сигнал
S(jω) – спектр, т.е. распределение комплексных амплитуд по частоте.
К реализации случайного процесса x(t) можно формально применить преобразование Фурье и вычислить ее спектр
Энергия реализации определяется выражением

При таком подходе когда Т→∞ энергия реализации неограниченно возрастает. Поэтому переходят от энергии реализации к средней мощности на интервале Т
где Sx(ω)/T - спектральная плотность средней мощности, т.е. средняя мощность, приходящаяся на единицу полосы частот.
Функция
характеризует энергетический спектр, т.е. распределение средней мощности по частоте
Дисперсия процесса Dx равна площади под кривой

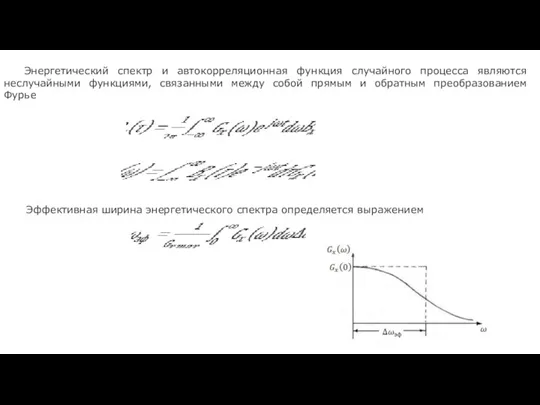
Энергетический спектр и автокорреляционная функция случайного процесса являются неслучайными функциями, связанными между собой прямым и обратным преобразованием Фурье
Эффективная ширина энергетического спектра определяется выражением

Автокорреляционная функция случайного процесса характеризует степень статистической связи между значениями процесса, разделенными интервалом времени τ
Значение τ, при котором значения случайного процесса x(t) и x(t+τ) становятся статистически несвязанными, называется интервалом корреляции
Cвязь между эффективной шириной спектра и интервалом корреляции
Отсюда

Noise & Random Processes
Mon, March 02
EE 495 Modern Navigation Systems
We can NOT describe all of the parameters that contribute to a signal or sensor measurement
Deterministic: Can exactly model the relationship between the input (stimulus) and output (sensor meas)
Random: Can NOT exactly model the relationship
Can characterize attributes of the signal
e.g., mean (μ), standard deviation (σ), probability density function (pdf), power spectral density (PSD), …
i.e., Noise (random signals)
Slide of 19

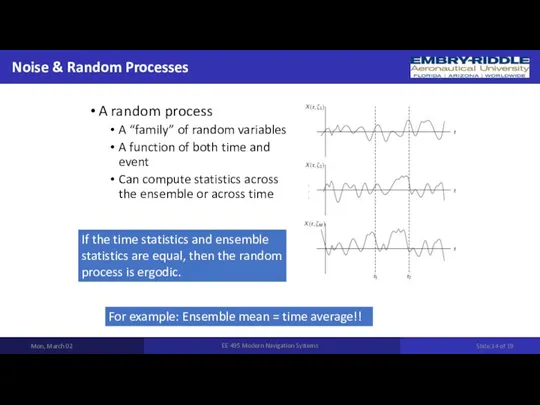
Noise & Random Processes
Mon, March 02
EE 495 Modern Navigation Systems
A random process
A “family” of random variables
A function of both time and event
Can compute statistics across the ensemble or across time
If the time statistics and ensemble statistics are equal, then the random process is ergodic.
For example: Ensemble mean = time average!!
Slide of 19

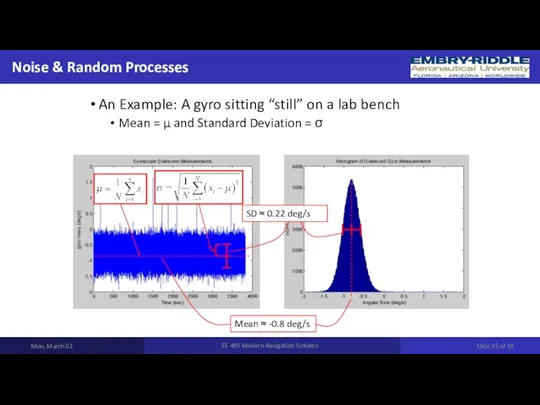
Noise & Random Processes
Mon, March 02
EE 495 Modern Navigation Systems
An Example: A gyro sitting “still” on a lab bench
Mean = μ and Standard Deviation = σ
Slide of 19