Содержание
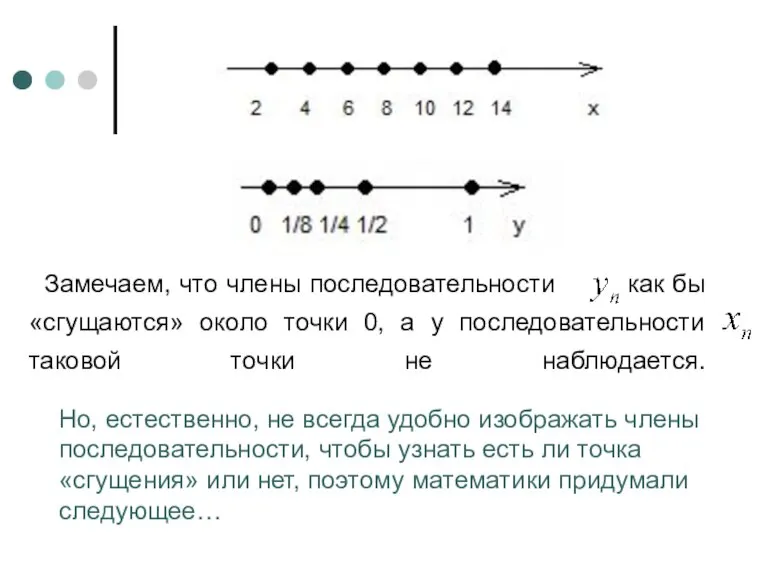
- 2. Предел числовой последовательности Рассмотрим две числовые последовательности: : 2, 4, 6, 8, 10, …, ,…; :
- 3. Замечаем, что члены последовательности как бы «сгущаются» около точки 0, а у последовательности таковой точки не
- 4. Определение 1. Пусть a - точка прямой, а r - положительное число. Интервал (a-r, a+r) называют
- 5. Теперь можно перейти к определению точки «сгущения», которую математики назвали «пределом последовательности». Например (-0.1, 0.5) –
- 6. Определение 2. Число называют пределом последовательности , если в любой заранее выбранной окрестности точки содержатся все
- 7. Комментарий Пусть . Возьмем окрестность точки r радиуса, r, то есть (b-r, b+r) . Тогда существует
- 8. Пример. Существует ли номер , начиная с которого все члены последовательности попадают в окрестность точки радиуса
- 9. Пример Существует ли номер n0, начиная с которого все члены последовательности (хn) попадают в окрестность точки
- 10. Практические задания 1. Запишите окрестность точки радиуса в виде интервала, если: 2. Окрестностью какой точки и
- 12. Скачать презентацию








 Ситуация успеха на уроках математики как средство повышения качества образования
Ситуация успеха на уроках математики как средство повышения качества образования Методика изучения объема
Методика изучения объема Матрицы
Матрицы Семейство четырехугольников
Семейство четырехугольников ЕГЭ 2014. Задачи первой и второй части (Вариант 43)
ЕГЭ 2014. Задачи первой и второй части (Вариант 43)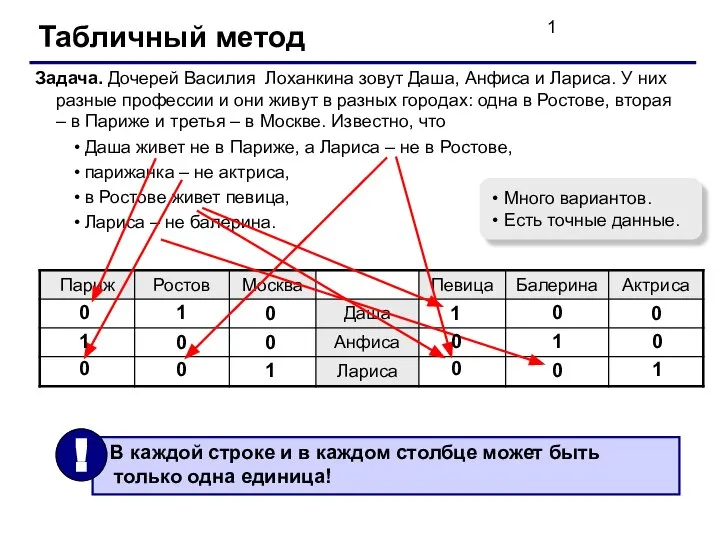 Табличный метод решения логических задач
Табличный метод решения логических задач Исследование корреляции
Исследование корреляции Вычислите логарифм. Практическая работа
Вычислите логарифм. Практическая работа Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже 2 погрешности ру с
2 погрешности ру с Значение переменной после выполнения алгоритма
Значение переменной после выполнения алгоритма Презентация на тему Вычисление объемов пространственных тел
Презентация на тему Вычисление объемов пространственных тел  Деление дробей. 6 класс
Деление дробей. 6 класс Свойства действий над числами
Свойства действий над числами Vorlesung. Blatt 2
Vorlesung. Blatt 2 Построение Сечения
Построение Сечения Преобразования неравенств
Преобразования неравенств Первый признак равенства треугольников
Первый признак равенства треугольников Презентация на тему Меры длинны Древней Руси
Презентация на тему Меры длинны Древней Руси  Презентация на тему Подготовка к ЕГЭ по математике
Презентация на тему Подготовка к ЕГЭ по математике  ВКР: Исследование нормального строения конечных групп
ВКР: Исследование нормального строения конечных групп Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Решение задач
Решение задач Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Математический квест Хакерская атака
Математический квест Хакерская атака Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Классификация оптимизационных задач
Классификация оптимизационных задач Квадрат. Основные свойства квадрата
Квадрат. Основные свойства квадрата