Слайд 2План вебинара
1)Разбор ДЗ
2) Интегралы:
неопределённые интегралы
определённые интегралы
3) Дифференциальные уравнения

Слайд 3Разбор ДЗ (ФНП). Часть 1.
1. Найти область определения функции.

Слайд 42. Найти частные производные 1-го порядка функции.

Слайд 63. Найти полный дифференциал функции в точке (1;1).

Слайд 94. Исследовать на экстремум функцию
Решение: https://www.wolframalpha.com/input/?i=extrema+calculator&assumption=%7B%22F%22%2C+%22GlobalExtremaCalculator%22%2C+%22curvefunction%22%7D+-%3E%22x%5E2%2Bxy%2By%5E2-6x-9y%22
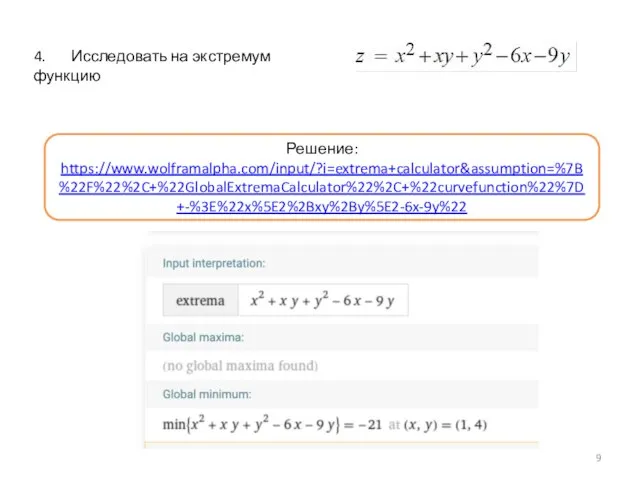
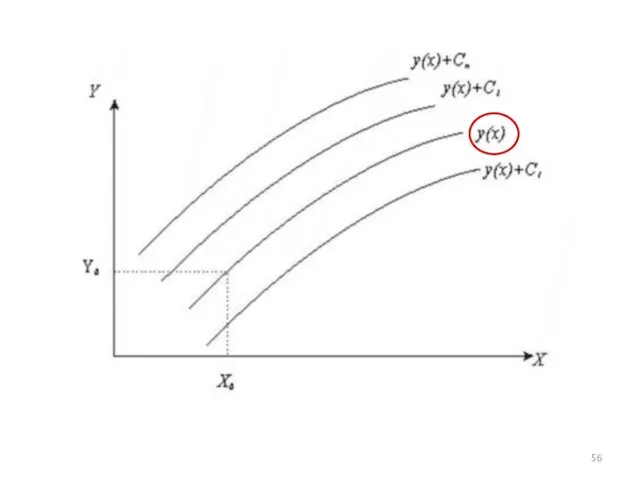
Слайд 11Приращение функции и приращение аргумента
Слайд 14Интегрирование
по сути, это противодействие дифференцированию.
Знак интегрирования:
SQUARE -> S ->

Слайд 15При интегрировании проверить себя довольно просто: достаточно взять производную от ответа -

должна получится функция под интегралом.
Слайд 20Весь процесс интегрирования сводится к тому, что необходимо привести подынтегральную функцию к

табличному виду.
Слайд 23Метод замены переменной
(по сути, он идентичен внесению под знак дифференциала)

Слайд 24В этом методе важно вернуться к исходной переменной:

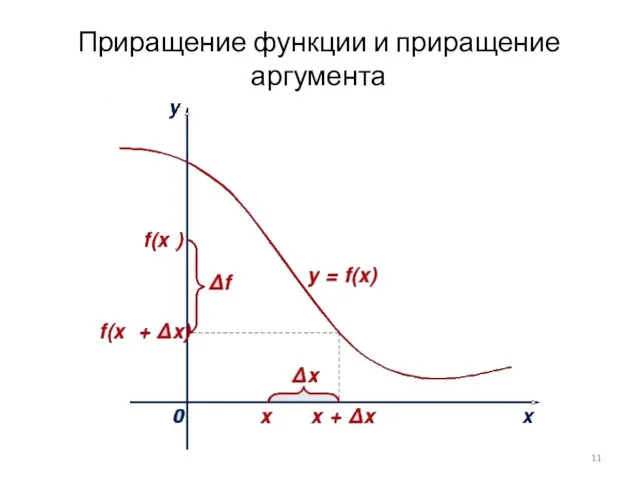
Слайд 27Интегрируем правую и левую части
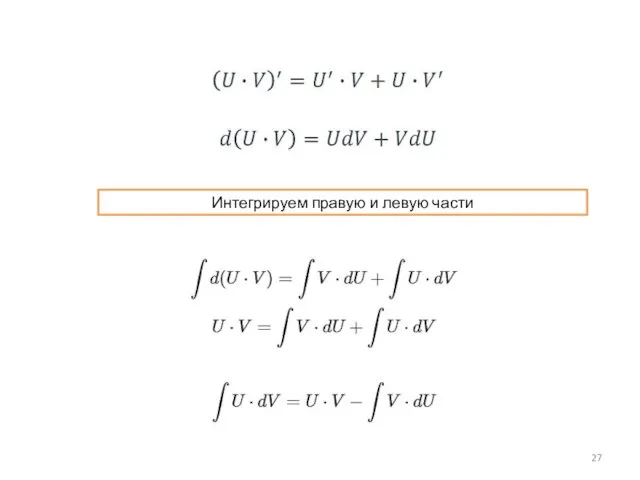
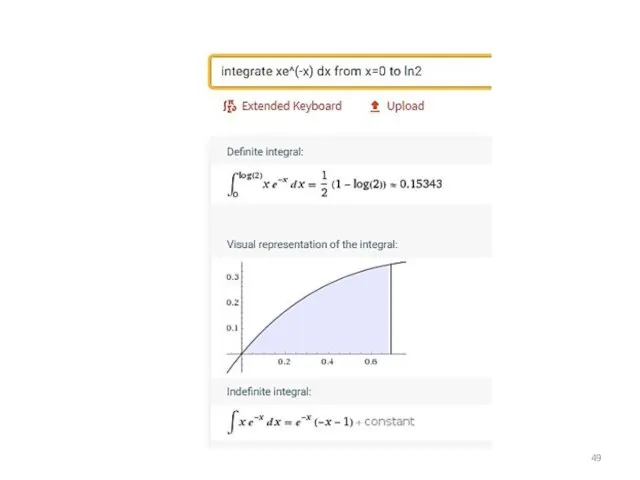
Слайд 31Какие интегралы берутся по частям

Слайд 32
Дробь правильная
(старшая степень выражения в знаменателе выше степени выражения в числителе)

Слайд 40 Для интеграла Римана функция должна быть непрерывна и дифференцируема во всех

точках заданного отрезка [a,b] . Для интеграла Лебега таких ограничений нет.
Т.е. интеграл Лебега совпадает с интегралом Римана там, где интеграл Римана существует. При этом интеграл Лебега можно брать и от не дифференцируемых в точке функций. Например, от функции Дирихле.
Слайд 41Интегрирование
по Риману
Интегрирование
по Лебегу
Слайд 42Статьи по интегралам Лебега
Интеграл Лебега: https://mathworld.wolfram.com/LebesgueIntegral.html
Мера Лебега:
https://mathworld.wolfram.com/Measure.html
Пример вычисления интеграла Лебега:
https://demonstrations.wolfram.com/LebesgueIntegration/

Слайд 50Несобственные интегралы
определённые интегралы с особенностями на границах.
Одна из границ -- бесконечность
Особенность на

одной из границ интегрирования
Слайд 51Примеры вычисления несобственных интегралов

Слайд 52Дифференциальные уравнения: где применяются.
DSP (Цифровая обработка сигналов)
Computer vision
«Анализ любых экспериментальных данных (зависимости

величин) - только диффуры! А это - весь мир». (c, @xmoonlight, https://qna.habr.com/q/149841)
Слайд 53Решение дифференциальных уравнений

Слайд 58Как определить, что ДУ однородное и использовать замену вида
смотрим тут
http://mathprofi.ru/odnorodnye_diffury_pervogo_poryadka.html






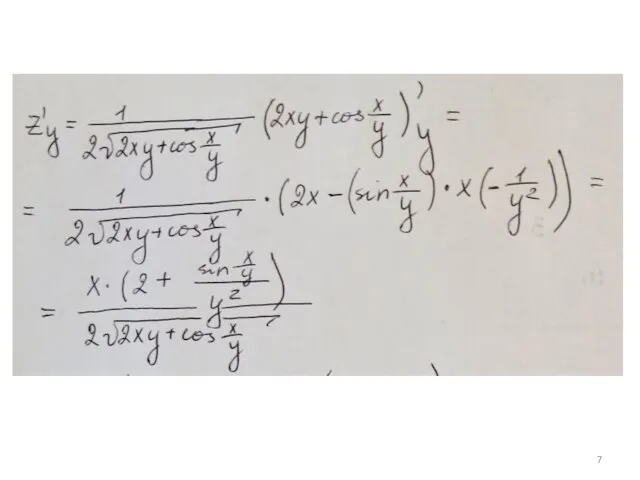





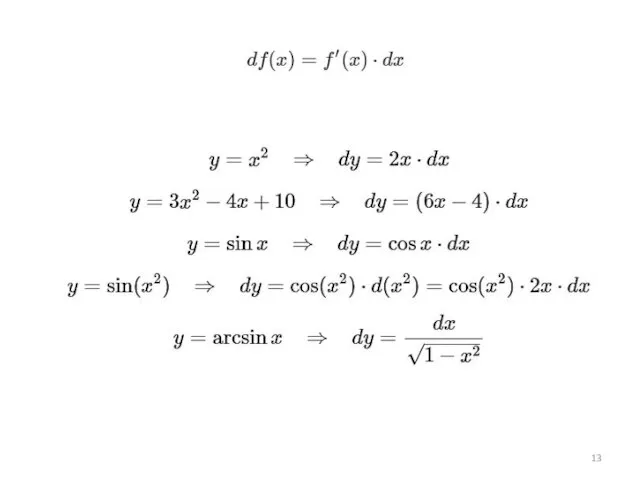


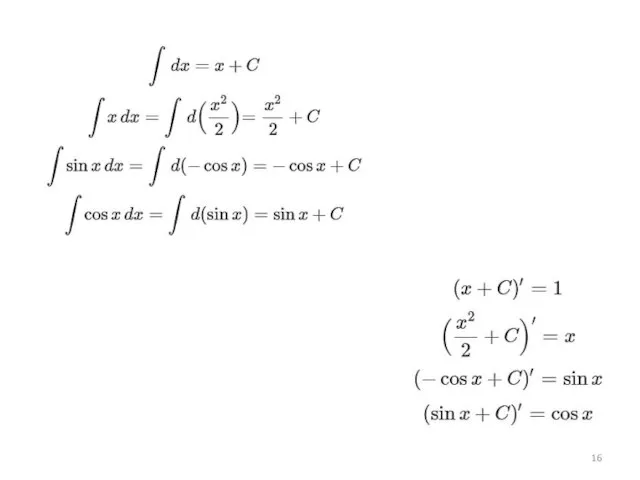








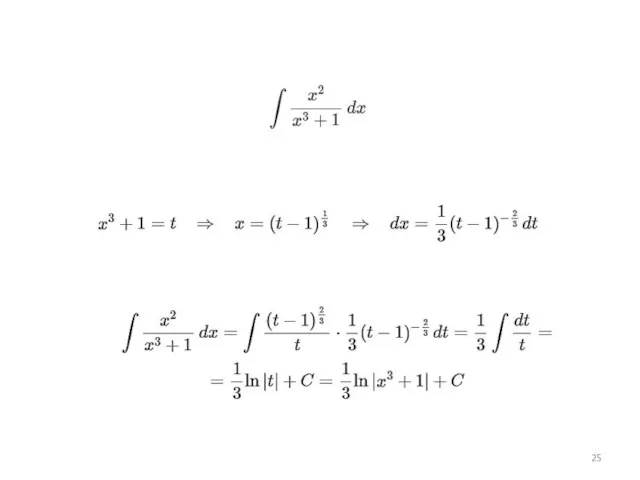

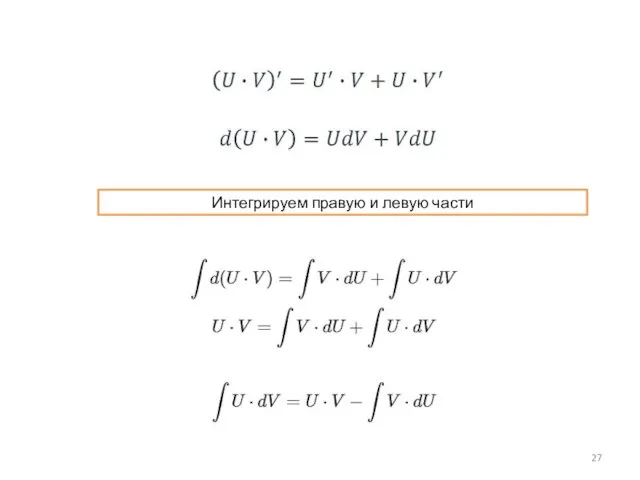

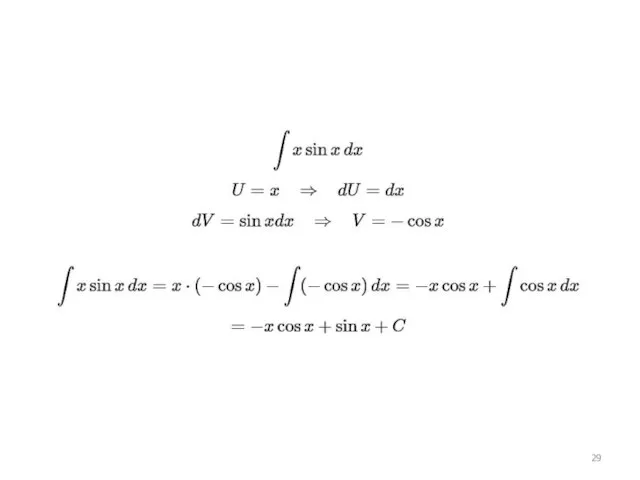














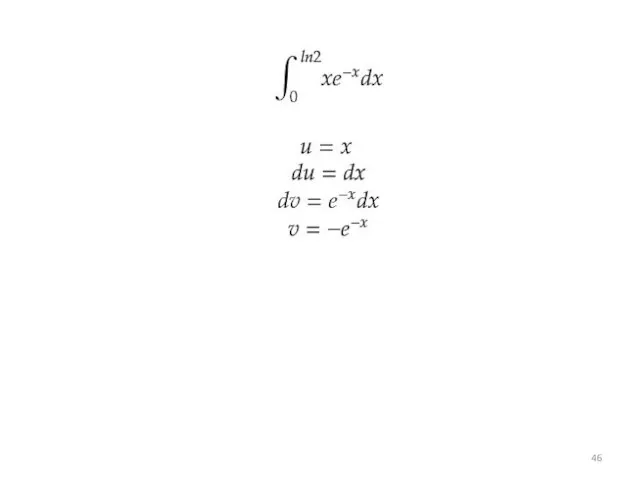

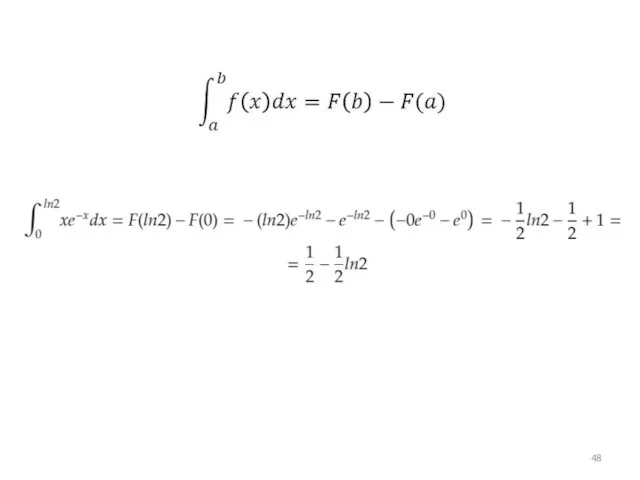








 Повторение. Свойства умножения. Свойства деления
Повторение. Свойства умножения. Свойства деления Математика. 1 класс
Математика. 1 класс Площадь фигуры. Сравнение площадей
Площадь фигуры. Сравнение площадей Векторы. Обобщающий урок
Векторы. Обобщающий урок Сложение и вычитание смешанных чисел. Графический диктант
Сложение и вычитание смешанных чисел. Графический диктант Частные случаи длины дуги. Лекция №10
Частные случаи длины дуги. Лекция №10 Нахождение корней уравнения методом деления отрезка пополам
Нахождение корней уравнения методом деления отрезка пополам Математические ребусы (1 класс)
Математические ребусы (1 класс) Конструирование фигур из кубов и прямоугольных параллелепипедов
Конструирование фигур из кубов и прямоугольных параллелепипедов Вынужденные гармонические колебания стержней с распределенной массой при изгибе
Вынужденные гармонические колебания стержней с распределенной массой при изгибе Погрешность результата измерения
Погрешность результата измерения Презентация на тему Деление чисел
Презентация на тему Деление чисел  Проекция группы геометрических тел
Проекция группы геометрических тел Математическая игра «Звездный час»
Математическая игра «Звездный час» Числовые функции
Числовые функции Задача 6.15 из сборника задач к начальному курсу эконометрики
Задача 6.15 из сборника задач к начальному курсу эконометрики Арифметические выражения
Арифметические выражения Решение Уравнений, содержащих модуль
Решение Уравнений, содержащих модуль Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Понятие вектора. Векторы на плоскости
Понятие вектора. Векторы на плоскости Площадь треугольника
Площадь треугольника Нахождение наибольшего и наименьшего значений функции на отрезке с помощью производной
Нахождение наибольшего и наименьшего значений функции на отрезке с помощью производной Понятие логарифма
Понятие логарифма Решение прямоугольных треугольников
Решение прямоугольных треугольников Роль дисплазии соединительной ткани в формировании остеопенического синдрома у детей
Роль дисплазии соединительной ткани в формировании остеопенического синдрома у детей Параллельность плоскостей
Параллельность плоскостей Методы статистического анализа литературных текстов
Методы статистического анализа литературных текстов Элективный курс. Алгебра 11 класс. Уроки 07-08
Элективный курс. Алгебра 11 класс. Уроки 07-08