- Главная
- Математика
- Интегрированный урок: Многогранники вокруг нас

Содержание
Слайд 2ИЗ ИСТОРИИ
Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона
ИЗ ИСТОРИИ
Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона

(427-347 до н. э.) "Тимаус". Поэтому правильные многогранники также называются платоновыми телами. Каждый из правильных многогранников, а всего их пять, Платон ассоциировал с четырьмя "земными" элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с "неземным" элементом - небом (додекаэдр).
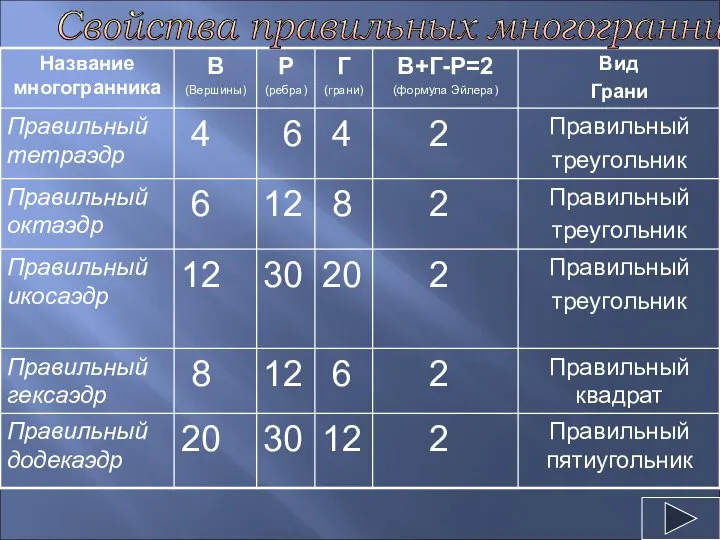
Слайд 3Свойства правильных многогранников
Свойства правильных многогранников
Слайд 4Огонь
ТЕТРАЭДР
Огонь
ТЕТРАЭДР

Слайд 5Вода
ИКОСАЭДР
Вода
ИКОСАЭДР

Слайд 6Воздух
ОКТАЭДР
Воздух
ОКТАЭДР

Слайд 7Земля
КУБ
Земля
КУБ

- Предыдущая
Арагон ў перыяд Высокага сярэднявеччаСледующая -
Гражданская оборона на объекте 3.2 Численные методы решения систем линейных алгебраических уравнений
3.2 Численные методы решения систем линейных алгебраических уравнений Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Симметрия 11кл
Симметрия 11кл Первый признак подобия треугольников. 8 класс
Первый признак подобия треугольников. 8 класс Следствия из аксиом I - III
Следствия из аксиом I - III Метод Гаусса для решения систем линейных уравнений
Метод Гаусса для решения систем линейных уравнений Презентация на тему Перпендикулярность прямой и плоскости
Презентация на тему Перпендикулярность прямой и плоскости  Прогрессия. Анзац
Прогрессия. Анзац Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Прямые на плоскости. Задачи 6 и 7
Прямые на плоскости. Задачи 6 и 7 Состав числа. Тренажер. Старшая группа
Состав числа. Тренажер. Старшая группа Введение в дисциплину Математические модели в экологических системах
Введение в дисциплину Математические модели в экологических системах Касательная к окружности. Свойства касательных к окружности
Касательная к окружности. Свойства касательных к окружности Построения в пространстве
Построения в пространстве Прямоугольный параллелепипед
Прямоугольный параллелепипед Тригонометриялық теңдеулерді шешу тәсілдерін үйрену
Тригонометриялық теңдеулерді шешу тәсілдерін үйрену Единицы измерения. Килограмм. Грамм
Единицы измерения. Килограмм. Грамм Площадь и периметр ромба
Площадь и периметр ромба Великий квадрат не знает пределов
Великий квадрат не знает пределов Матрицы. Действия над матрицами
Матрицы. Действия над матрицами Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Треугольники. Задача
Треугольники. Задача Фигуры. Геометрия
Фигуры. Геометрия С чего начать подготовку к ЕГЭ по профильной математике
С чего начать подготовку к ЕГЭ по профильной математике Деление одночлена на одночлен. 7 класс. Урок 49
Деление одночлена на одночлен. 7 класс. Урок 49 Кривые Безье
Кривые Безье