Содержание
- 2. Задание Записать план исследования функции Исследовать функцию и построить ее график.
- 3. Область определения функции Определение. Областью определения функции называется множество значений независимой переменной, при которых функция определена.
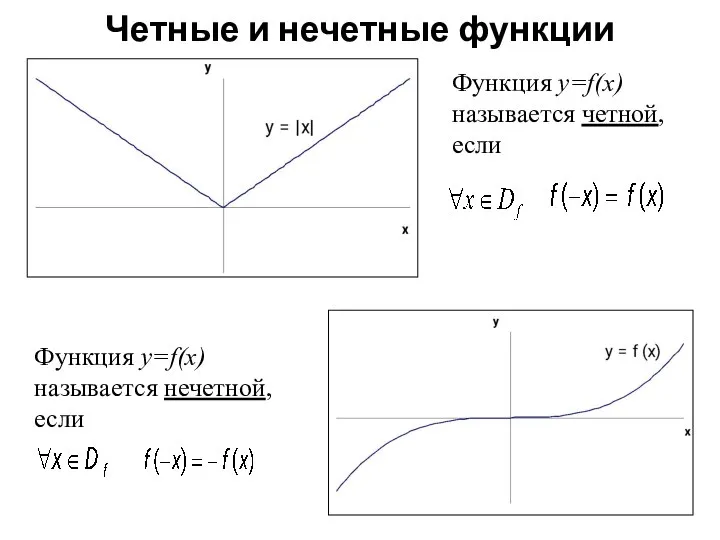
- 4. Четные и нечетные функции Функция y=f(x) называется четной, если Функция y=f(x) называется нечетной, если
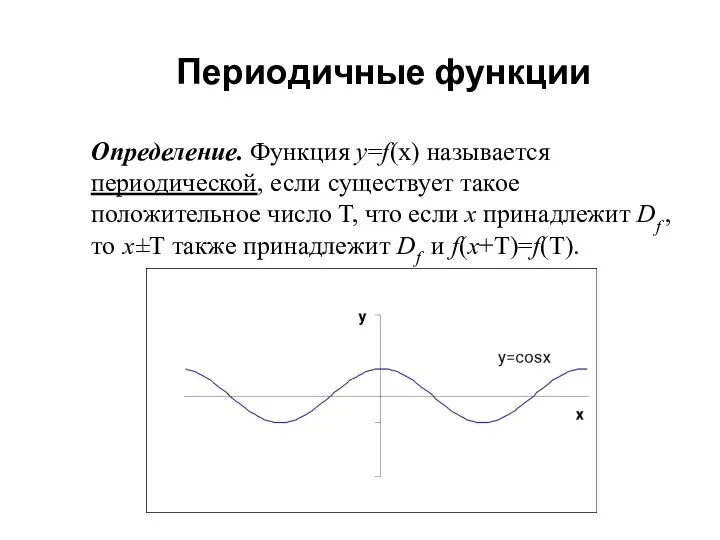
- 5. Периодичные функции Определение. Функция y=f(x) называется периодической, если существует такое положительное число Т, что если х
- 6. Точки пересечения с осями координат При исследовании функции необходимо найти координаты точек пересечения графика функции с
- 7. Непрерывность. Характер точек разрыва Функция у=f(x) называется непрерывной в точке х0, если функция определена в точке
- 8. Точки разрыва функции Определение. Точкой разрыва функции называется точка из области определения функции, в которой функция
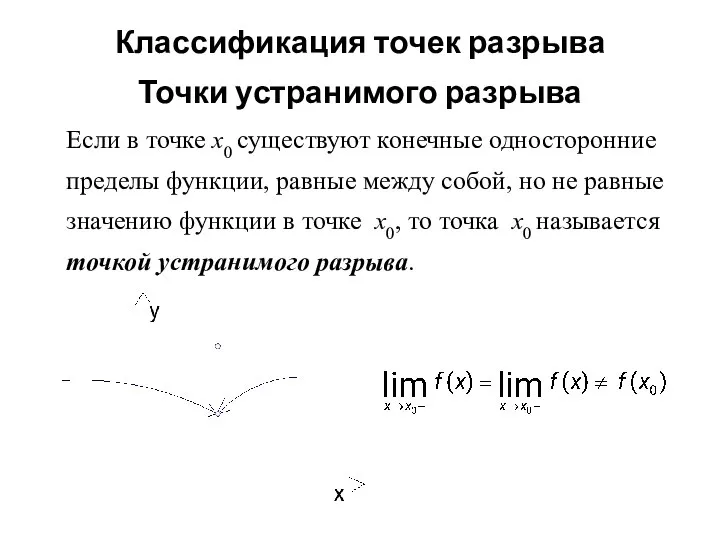
- 9. Классификация точек разрыва Точки устранимого разрыва Если в точке х0 существуют конечные односторонние пределы функции, равные
- 10. Классификация точек разрыва Точки скачка Если в точке х0 существуют конечные односторонние пределы функции, не равные
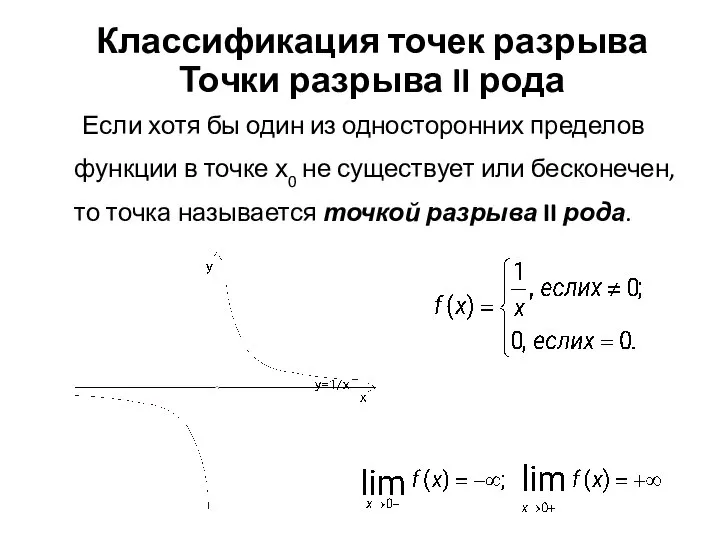
- 11. Классификация точек разрыва Точки разрыва II рода Если хотя бы один из односторонних пределов функции в
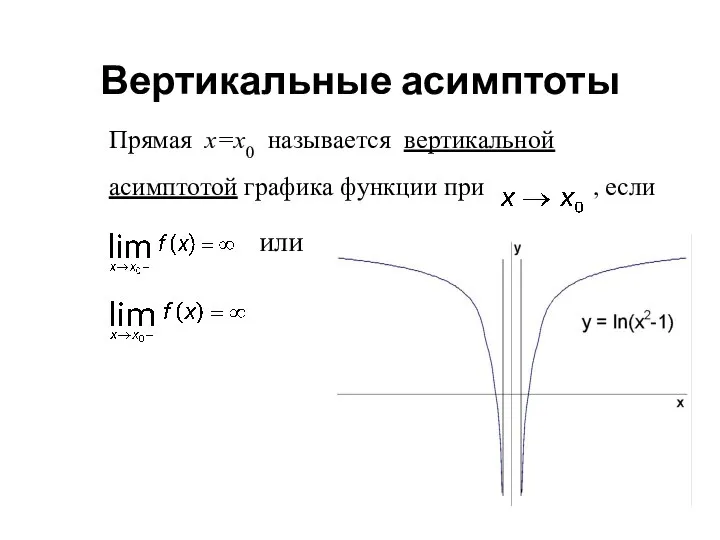
- 12. Вертикальные асимптоты Прямая х=х0 называется вертикальной асимптотой графика функции при , если или
- 13. Наклонные асимптоты Если существует прямая y=kx+b такая, что , то эта прямая называется асимптотой графика функции
- 14. Экстремумы функции Пусть функция f (x) определена и непрерывна на интервале (а, b). Точка х0 интервала
- 15. Исследование функции на монотонность Критические точки функции х=±1. f '(x)>0 при х 1; f '(x) функция
- 16. Выпуклость функции Функция у=f(х), определенная на интервале (а, b), называется выпуклой вверх (вниз) в интервале (а,
- 17. Выпуклость функции. Точки перегиба Если график функции в точке (х0, f(x0)) переходит с одной стороны касательной
- 18. Достаточные условия выпуклости функции и существования точек перегиба Достаточное условие строгой выпуклости функции Если на интервале
- 19. Пример. Исследуем функцию f(x) = (x2 – 2x)ex и построим её график. D(f) = R, поскольку
- 20. Будем искать наклонные асимптоты в виде y = kx + b. Коэффициент k найдём по формуле:
- 21. Теперь найдём значение b по формуле . Имеем: Таким образом, k=0 и b=0, так что при
- 22. Знак функции определяется множителем x2 – 2x, поскольку ex >0 при всех x. Значит, f(x)>0 при
- 23. Значение функции в этой точке равно В точке √2 убывание сменяется возрастанием, значит, точка √2 -
- 24. Становится очевидно, что область значений функции -- это По эскизу графика видно, что где-то в местах,
- 26. Скачать презентацию


















 Свойства логарифмов
Свойства логарифмов Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Координатная плоскость
Координатная плоскость Показательные и логарифмические уравнения, системы, неравенства
Показательные и логарифмические уравнения, системы, неравенства Числа 6 и 7. Письмо цифры 7 (1 класс)
Числа 6 и 7. Письмо цифры 7 (1 класс) Справочник по геометрии
Справочник по геометрии Презентация на тему Высказывания со словами: есть, существует, некоторые
Презентация на тему Высказывания со словами: есть, существует, некоторые  Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши)
Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши) Решение задач по теме: Объем цилиндра 11 класс
Решение задач по теме: Объем цилиндра 11 класс Распределительное свойства умножения
Распределительное свойства умножения Общее решение неполного квадратного уравнения. 8 класс
Общее решение неполного квадратного уравнения. 8 класс Задания по геометрии
Задания по геометрии Составление алгоритма
Составление алгоритма Конус
Конус Логарифмические уравнения
Логарифмические уравнения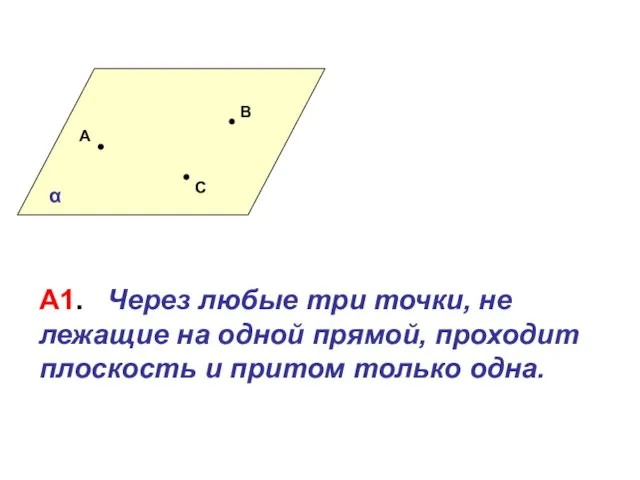 Плоскости
Плоскости Комплексные числа и действия над ними
Комплексные числа и действия над ними Найди значение выражений
Найди значение выражений Размерность. Единицы измерения
Размерность. Единицы измерения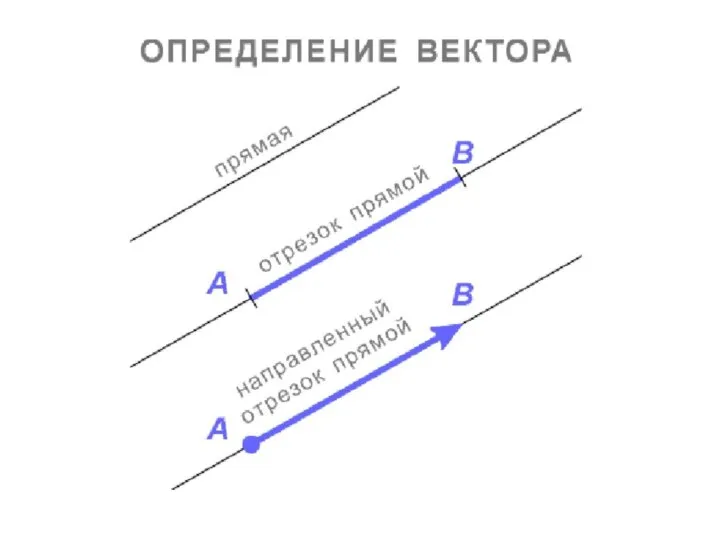 Определение вектора
Определение вектора Закрепление изученного. Решение задач
Закрепление изученного. Решение задач Понятие цилиндра
Понятие цилиндра Коэффициент корреляции
Коэффициент корреляции Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3
Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3 Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Системы степенных неравенств
Системы степенных неравенств