Содержание
- 3. Сходства и отличия квадрата и куба
- 4. Сходства и отличия квадрата и куба
- 5. Куб — геометрическое тело, каждая грань которого представляет собой квадрат. Из словаря:
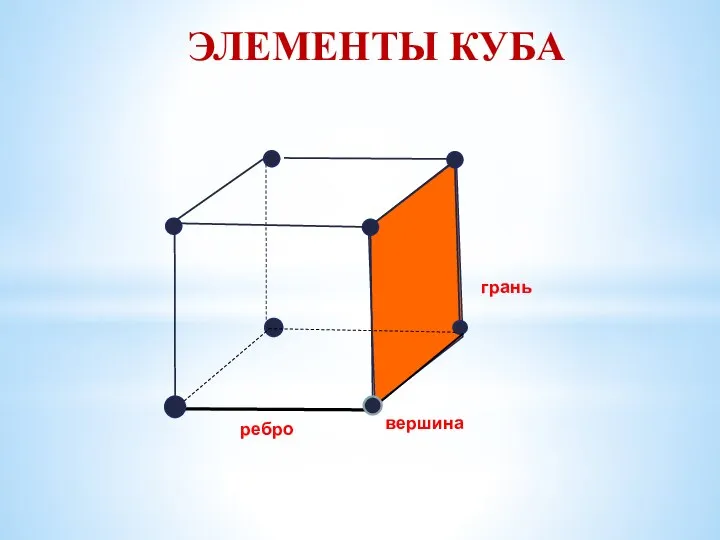
- 6. ЭЛЕМЕНТЫ КУБА грань вершина ребро
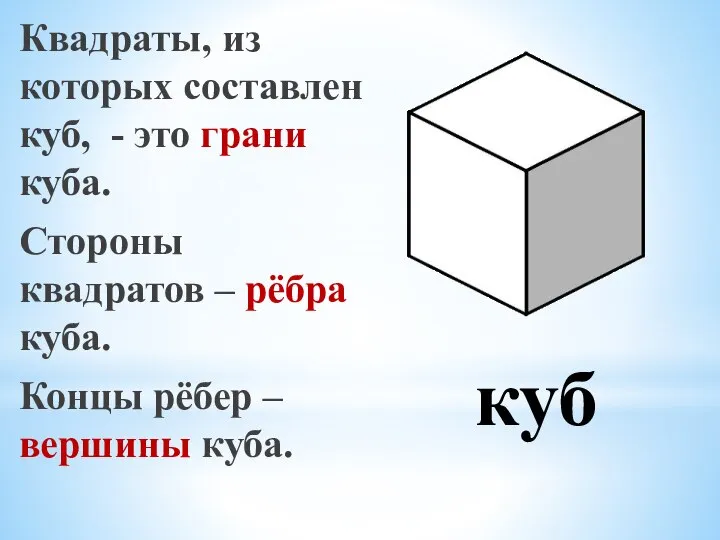
- 7. Квадраты, из которых составлен куб, - это грани куба. Стороны квадратов – рёбра куба. Концы рёбер
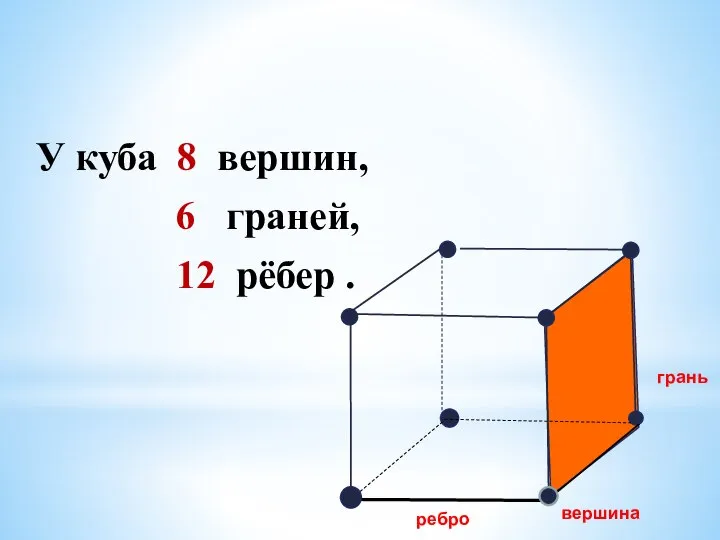
- 8. У куба 8 вершин, 6 граней, 12 рёбер . грань вершина ребро
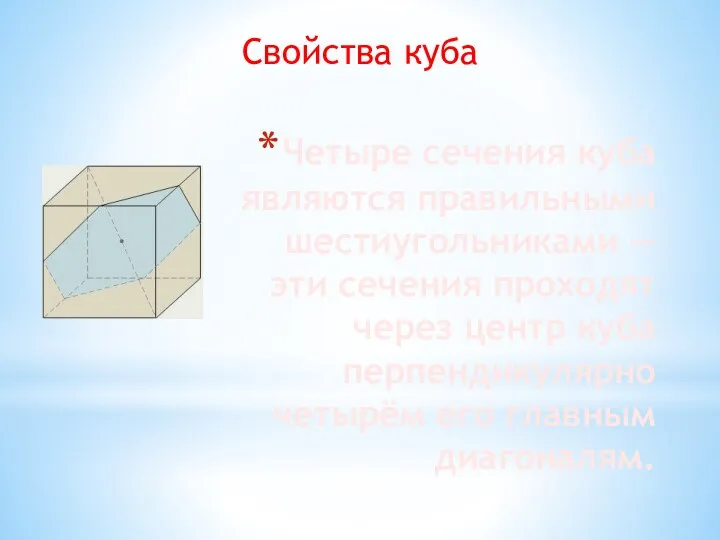
- 9. Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его
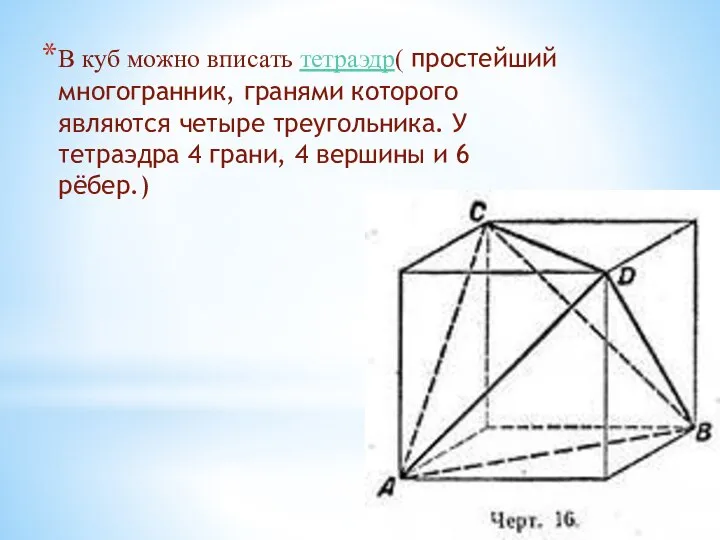
- 10. В куб можно вписать тетраэдр( простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани,
- 11. А) В куб можно вписать октаэдр(один из пяти выпуклых правильных многогранников, так называемых Платоновых тел.), притом
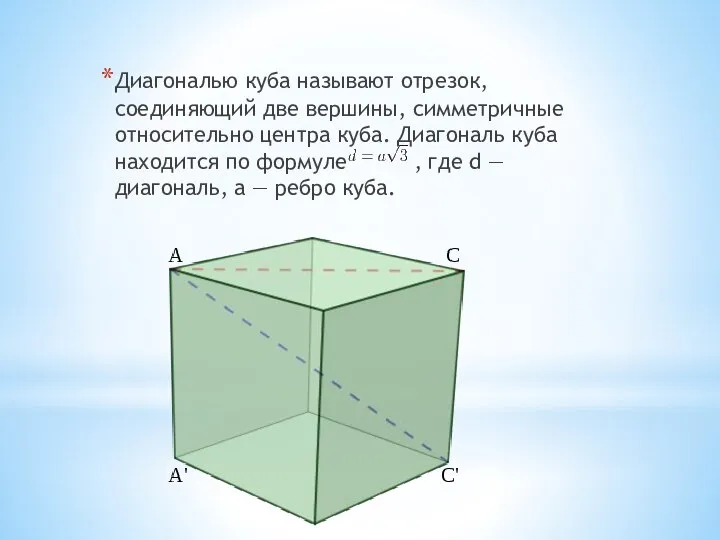
- 12. Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Диагональ куба находится по формуле
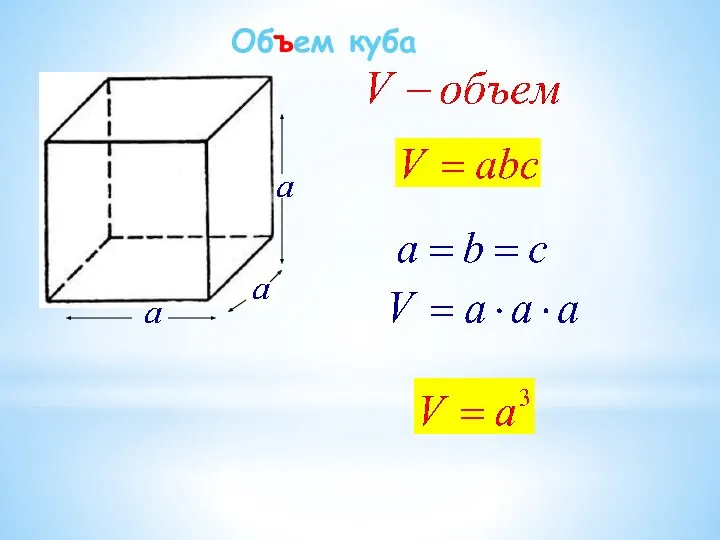
- 13. Объем куба
- 14. Формула для нахождения площади поверхности куба: S=
- 15. Задача №1 Площадь полной поверхности куба равна 24 см². Найдите его объем. Задача №2 Длина ребра
- 17. Скачать презентацию







 Урок геометрии в 7 классе Искусство рассуждать
Урок геометрии в 7 классе Искусство рассуждать Проверочная работа
Проверочная работа Формулы двойного аргумента
Формулы двойного аргумента Функции и их графики
Функции и их графики Презентация на тему Занимательная математика (4 класс)
Презентация на тему Занимательная математика (4 класс)  Несобственные интегралы второго рода
Несобственные интегралы второго рода Числовая последовательность
Числовая последовательность Сигнальные карточки
Сигнальные карточки Презентация на тему Функция y=x2
Презентация на тему Функция y=x2  Площадь треугольника
Площадь треугольника Представление информации. Решение задач на проценты
Представление информации. Решение задач на проценты Рациональные уравнения
Рациональные уравнения Рене Декарт (1596 -1650)
Рене Декарт (1596 -1650) Математика. Задачи
Математика. Задачи На лесной поляне
На лесной поляне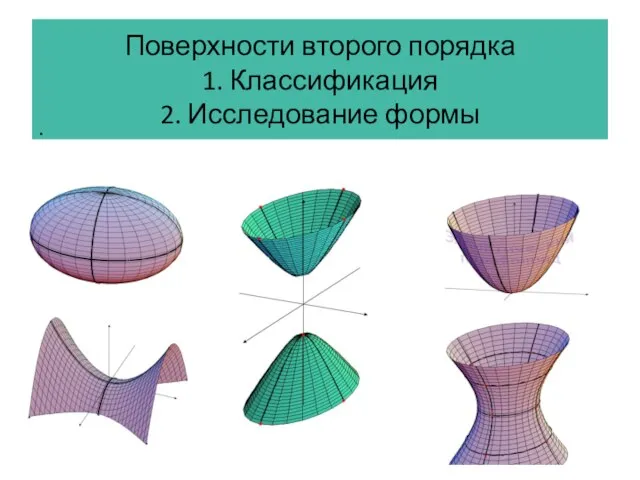 Поверхности второго порядка
Поверхности второго порядка Признаки равенства треугольников
Признаки равенства треугольников Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем Метод резолюций в алгебре высказываний
Метод резолюций в алгебре высказываний Ломаная линия. Обозначение ломаной
Ломаная линия. Обозначение ломаной Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Начальные геометрические сведения. Признаки равенства треугольников
Начальные геометрические сведения. Признаки равенства треугольников Состав 12 и 11. Карточки
Состав 12 и 11. Карточки Шаблон презентации по математике
Шаблон презентации по математике Иррациональные уравнения
Иррациональные уравнения Презентация на тему Объём многогранника
Презентация на тему Объём многогранника  Составление текстовых задач по математике , связанные с историей, литературой, географией и др
Составление текстовых задач по математике , связанные с историей, литературой, географией и др Эта загадочная Бутылка Клейна
Эта загадочная Бутылка Клейна