Содержание
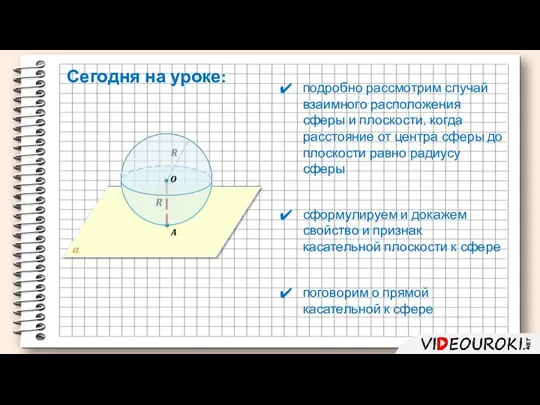
- 2. подробно рассмотрим случай взаимного расположения сферы и плоскости, когда расстояние от центра сферы до плоскости равно
- 3. Определение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
- 4. В зависимости от соотношения расстояния от центра сферы до плоскости и радиуса сферы возможны три случая
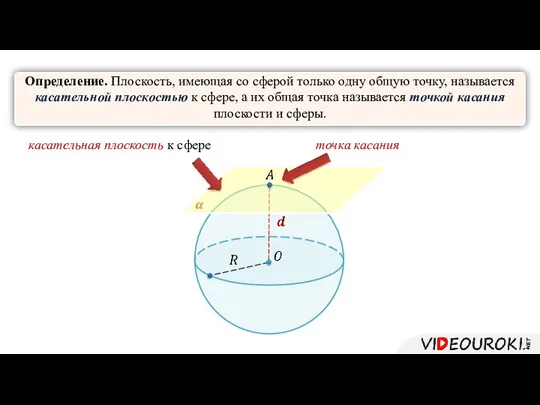
- 5. Определение. Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их
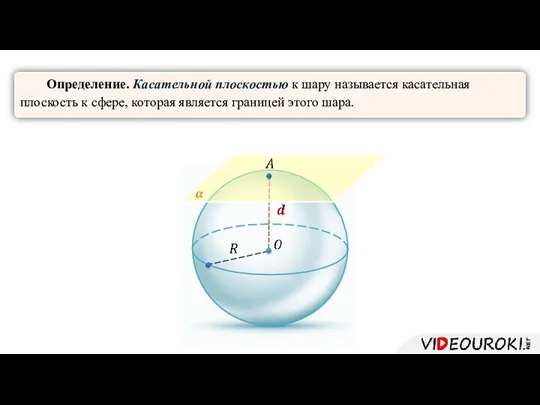
- 6. Определение. Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.
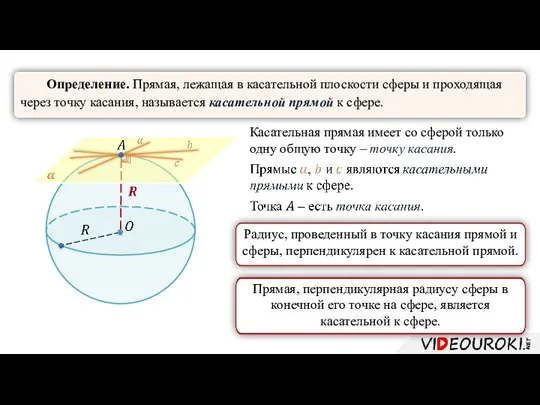
- 7. Теорема (свойство касательной плоскости к сфере). Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен
- 8. Обратная теорема (признак касательной плоскости к сфере). Если радиус сферы перпендикулярен к плоскости, проходящей через его
- 9. Решение.
- 10. Решение. В равностороннем треугольнике высота является и биссектрисой, и медианой.
- 11. Определение. Прямая, лежащая в касательной плоскости сферы и проходящая через точку касания, называется касательной прямой к
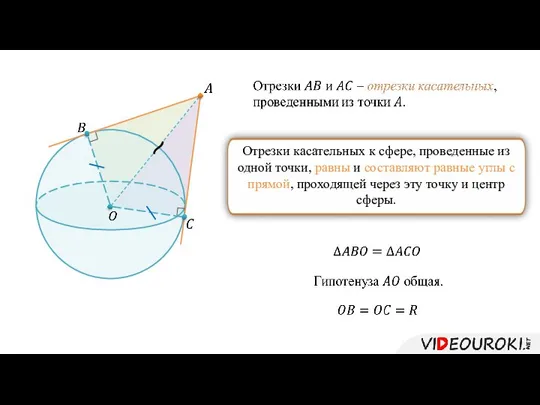
- 12. Отрезки касательных к сфере, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей
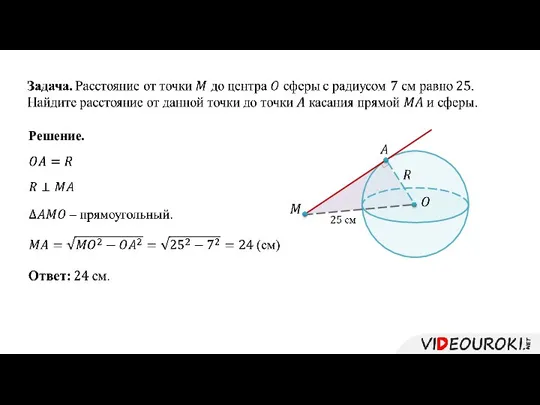
- 13. Решение.
- 15. Скачать презентацию






 Квадратичная функция и ее график
Квадратичная функция и ее график Классификация систем массового обслуживания
Классификация систем массового обслуживания Deterministic finite automata. Nondeterministic finite automata
Deterministic finite automata. Nondeterministic finite automata Математическая интеллектуальная игра для всей семьи
Математическая интеллектуальная игра для всей семьи urok_1_10_klass_geom
urok_1_10_klass_geom Формулы площади
Формулы площади Множество и его элементы
Множество и его элементы Статистический опрос жителей Санкт-Петербурга о применении ими пиротехнических изделий
Статистический опрос жителей Санкт-Петербурга о применении ими пиротехнических изделий Презентация на тему Приемы доказательства неравенств, содержащих переменные
Презентация на тему Приемы доказательства неравенств, содержащих переменные  Геометрические тела. 9 класс
Геометрические тела. 9 класс Статистика оплаты труда. Статистическое изучение фонда заработной платы и фонда материального поощрения
Статистика оплаты труда. Статистическое изучение фонда заработной платы и фонда материального поощрения Режим поступления заявок
Режим поступления заявок Презентация на тему Письменное умножение на двузначное число (4 класс)
Презентация на тему Письменное умножение на двузначное число (4 класс)  Основы тригонометрии. Упражнения
Основы тригонометрии. Упражнения Римские Числа Копылова Ольга 6 класс
Римские Числа Копылова Ольга 6 класс Морское путешествие
Морское путешествие Вероятность случайного события. Математика
Вероятность случайного события. Математика Час занимательной математики
Час занимательной математики Частные случаи длины дуги. Лекция №10
Частные случаи длины дуги. Лекция №10 Законы булевой алгебры
Законы булевой алгебры Свойство описанного четырехугольника
Свойство описанного четырехугольника Производная элементарных функций
Производная элементарных функций 20140130_dekada
20140130_dekada Решение уравнений
Решение уравнений Критические точки функции
Критические точки функции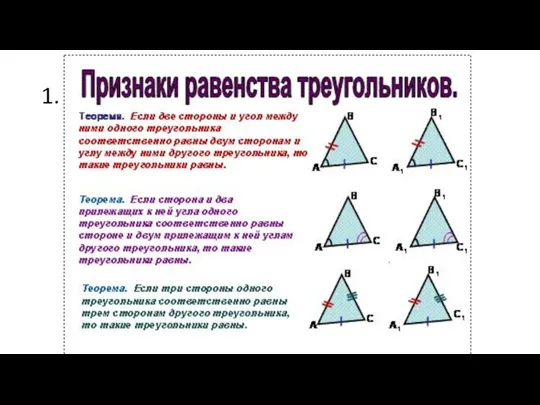 Признаки равенства треугольников
Признаки равенства треугольников Рациональные дроби и их свойства
Рациональные дроби и их свойства Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число