- Главная
- Математика
- Презентация на тему ВЕКТОРНАЯ АЛГЕБРА

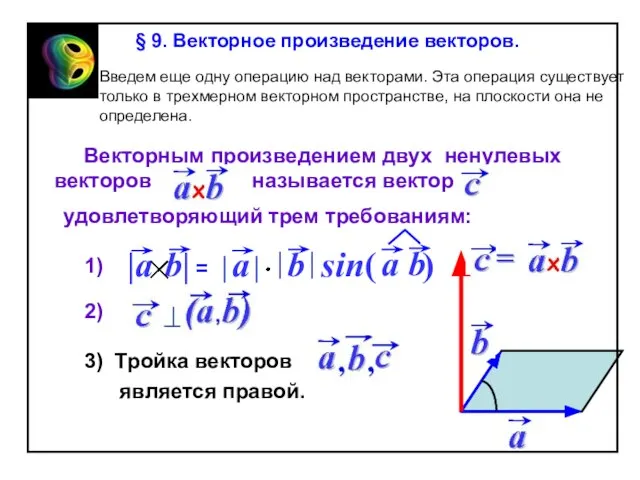
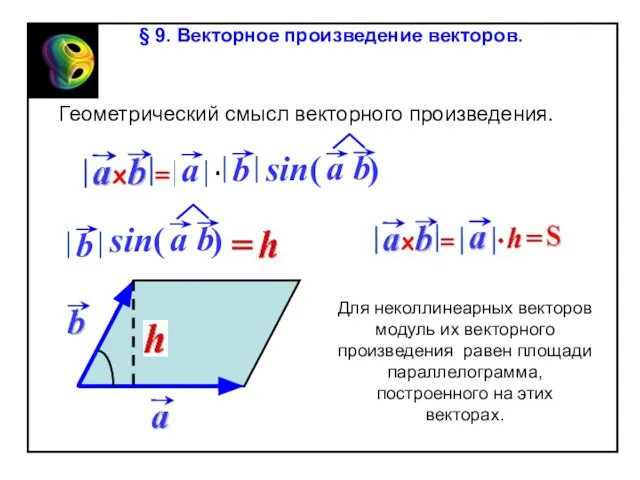
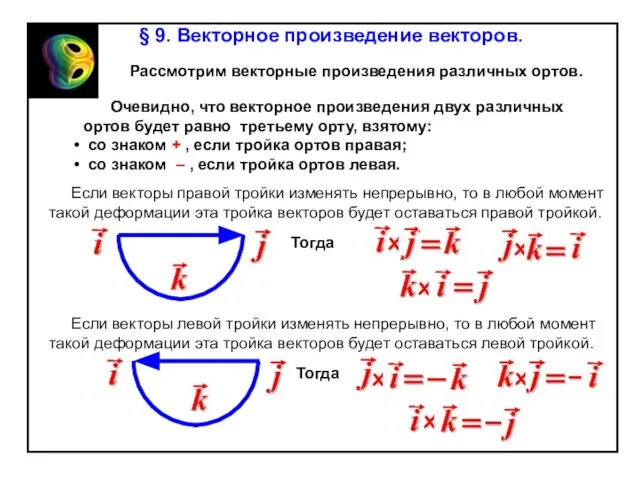
Содержание
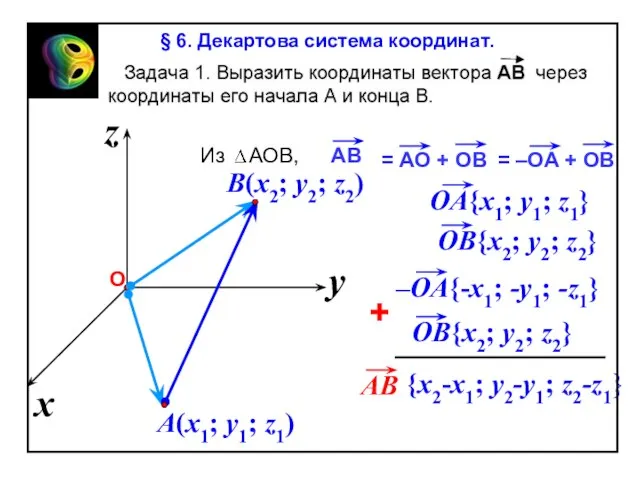
- 11. Если точка А – начало вектора , то говорят, что вектор отложен от точки А От
- 57. x z y Вычисление длины вектора по его координатам OA2= OA12 + OA22 + OA32 По
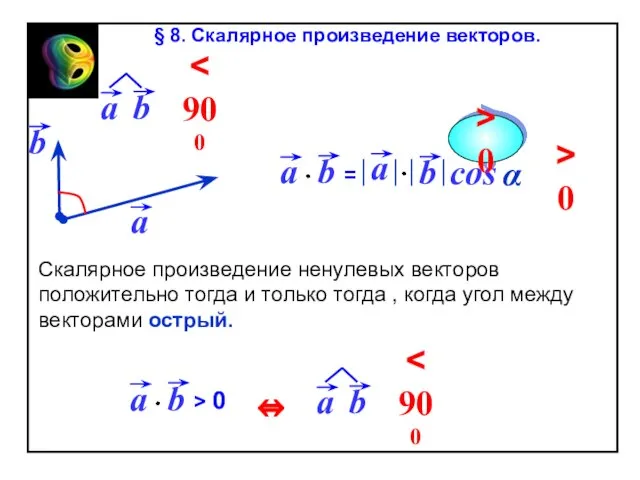
- 65. cos Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой.
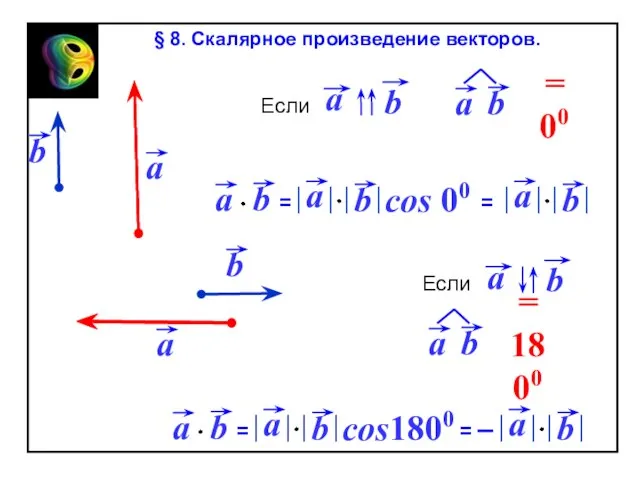
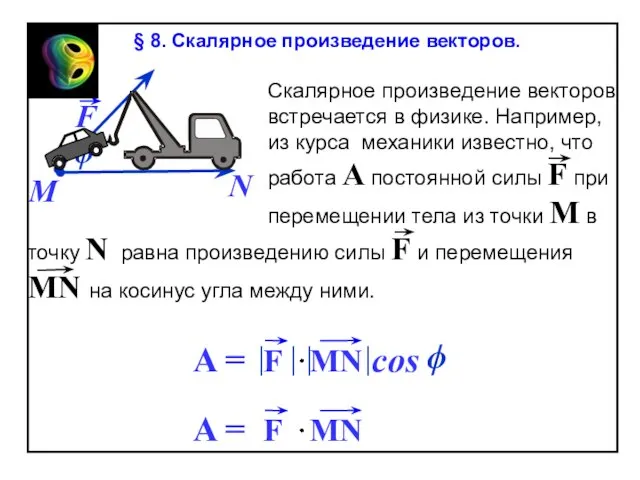
- 66. cos 00 cos1800 § 8. Скалярное произведение векторов.
- 99. Скачать презентацию
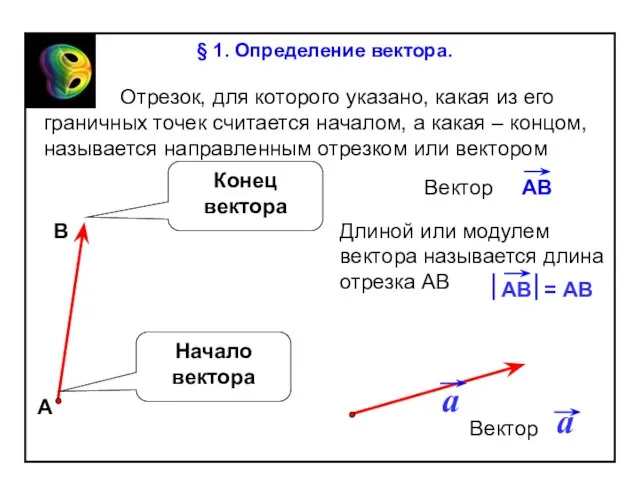
Слайд 11 Если точка А – начало вектора , то говорят, что
Если точка А – начало вектора , то говорят, что
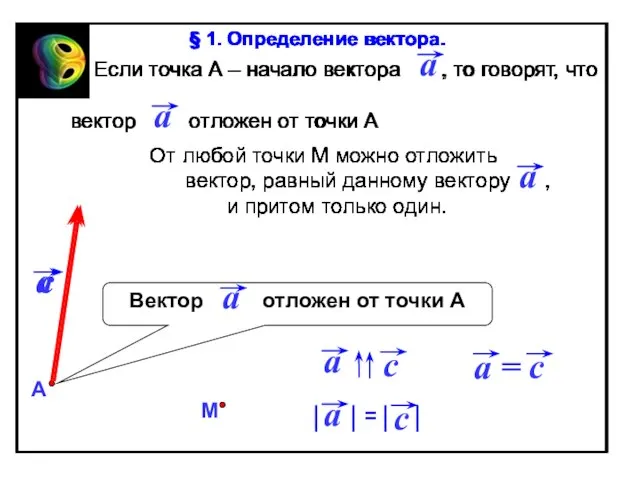
От любой точки М можно отложить
вектор, равный данному вектору ,
и притом только один.
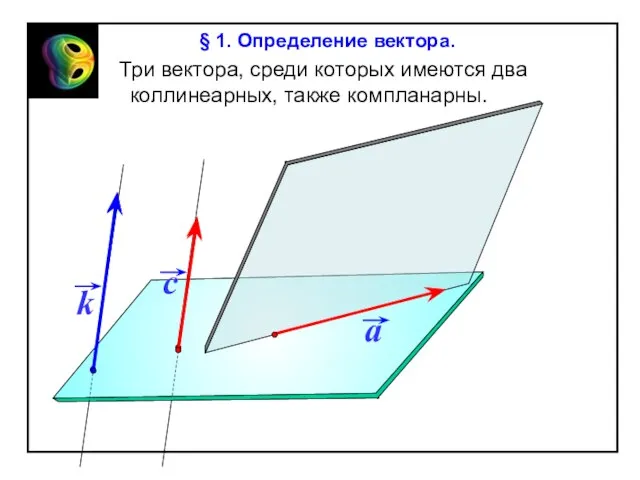
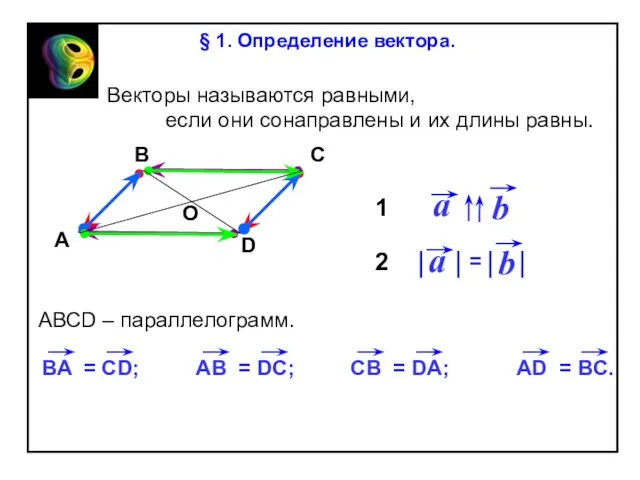
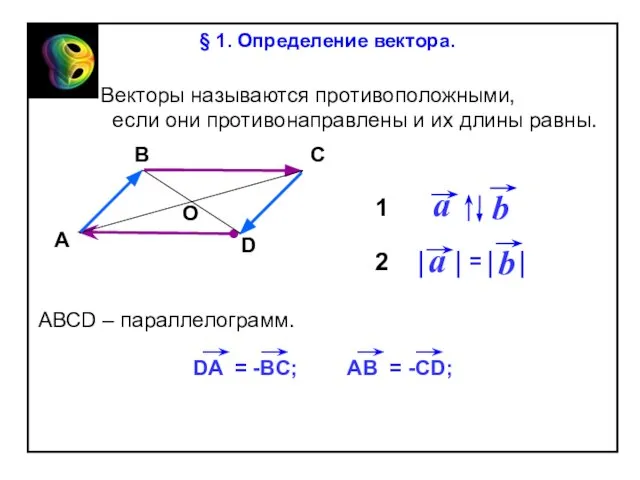
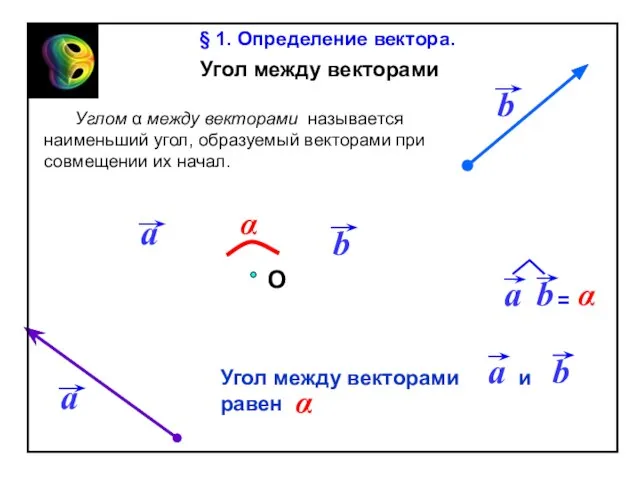
§ 1. Определение вектора.
Если точка А – начало вектора , то говорят, что
вектор отложен от точки А
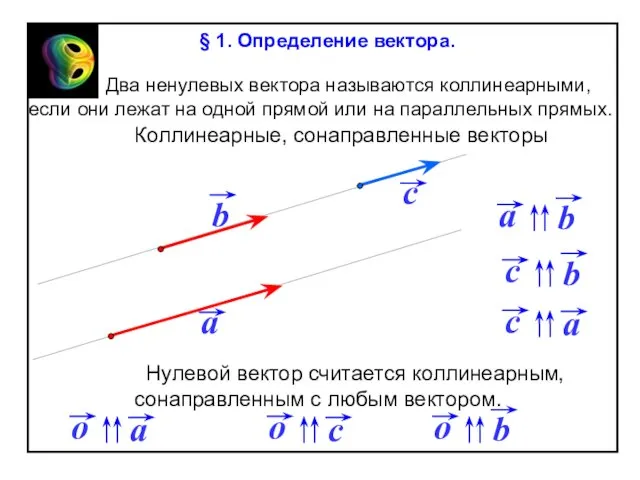
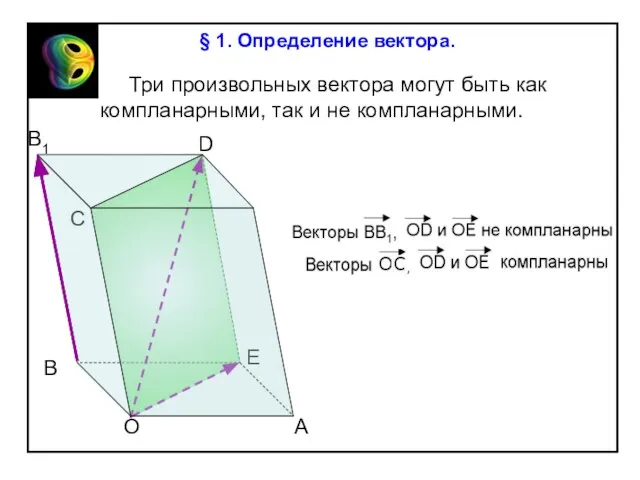
§ 1. Определение вектора.
От любой точки М можно отложить
вектор, равный данному вектору ,
и притом только один.
Если точка А – начало вектора , то говорят, что
вектор отложен от точки А
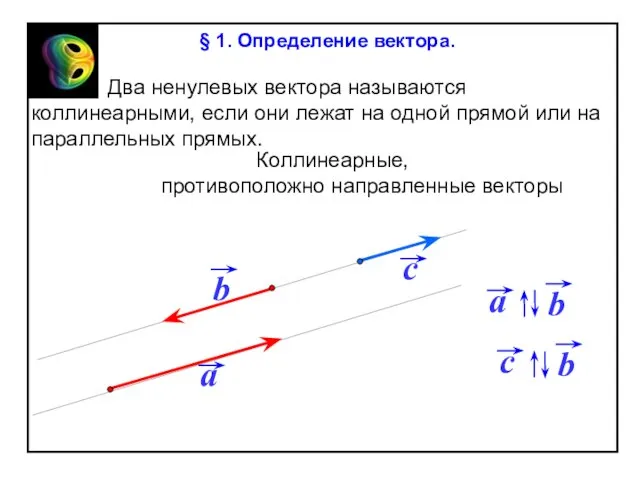
§ 1. Определение вектора.
От любой точки М можно отложить
вектор, равный данному вектору ,
и притом только один.
Если точка А – начало вектора , то говорят, что
вектор отложен от точки А
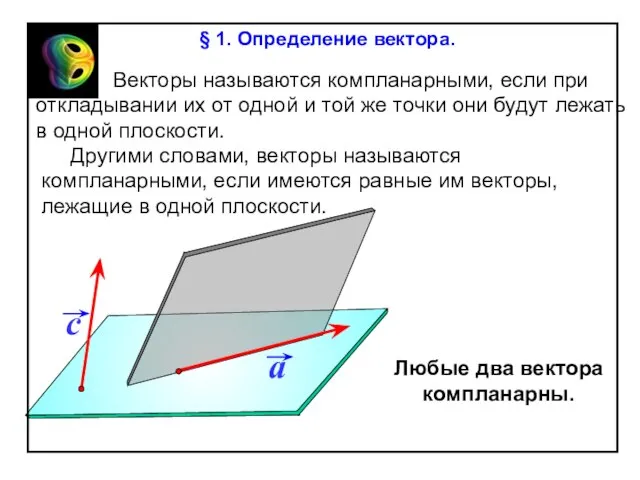
§ 1. Определение вектора.
От любой точки М можно отложить
вектор, равный данному вектору ,
и притом только один.
От любой точки М можно отложить
вектор, равный данному вектору ,
и притом только один.
Если точка А – начало вектора , то говорят, что
вектор отложен от точки А
От любой точки М можно отложить
вектор, равный данному вектору ,
и притом только один.
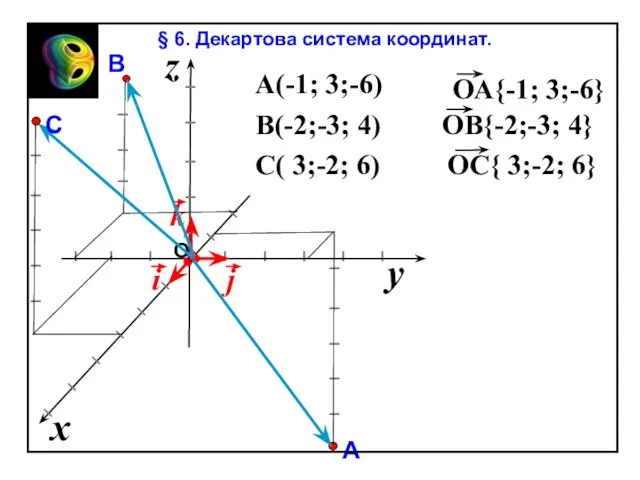
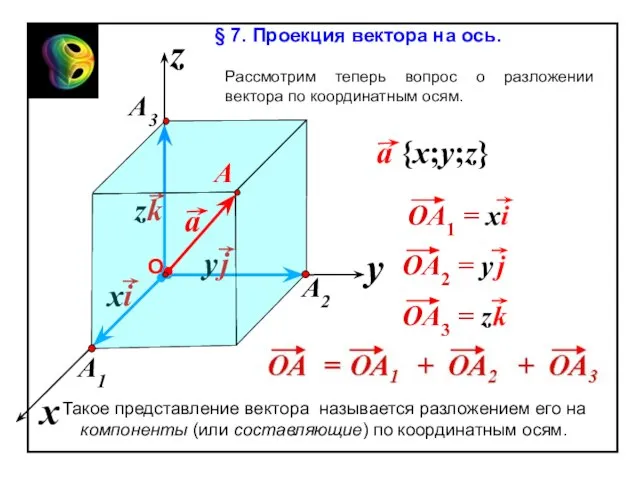
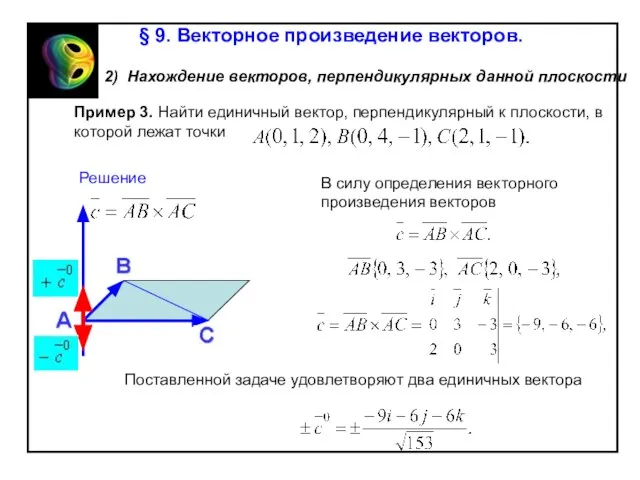
Слайд 57x
z
y
Вычисление длины вектора по его координатам
OA2= OA12 + OA22 + OA32
По
x
z
y
Вычисление длины вектора по его координатам
OA2= OA12 + OA22 + OA32
По
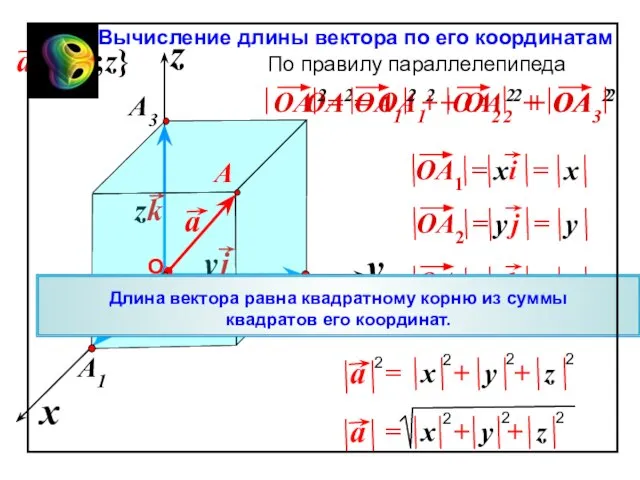
=
=
=
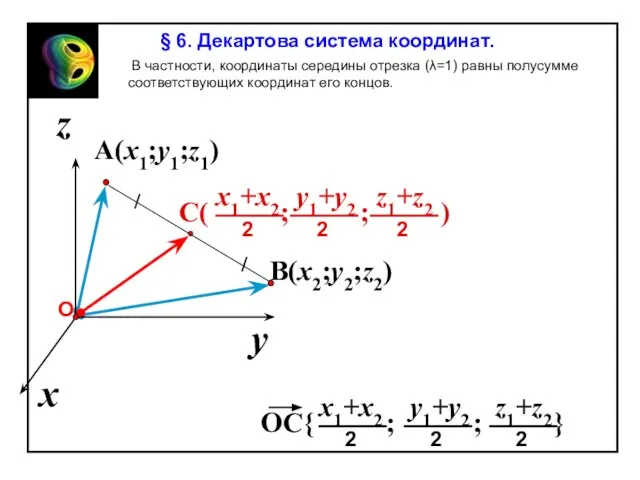
Длина вектора равна квадратному корню из суммы
квадратов его координат.
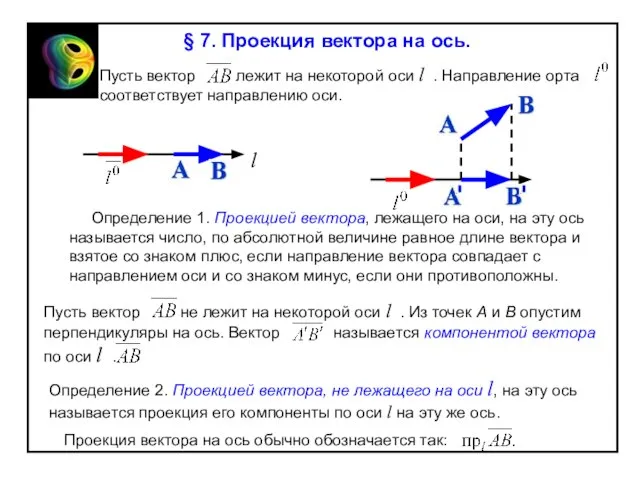
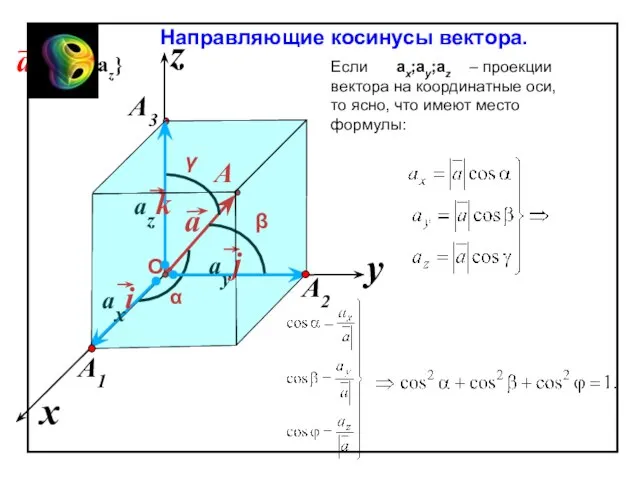
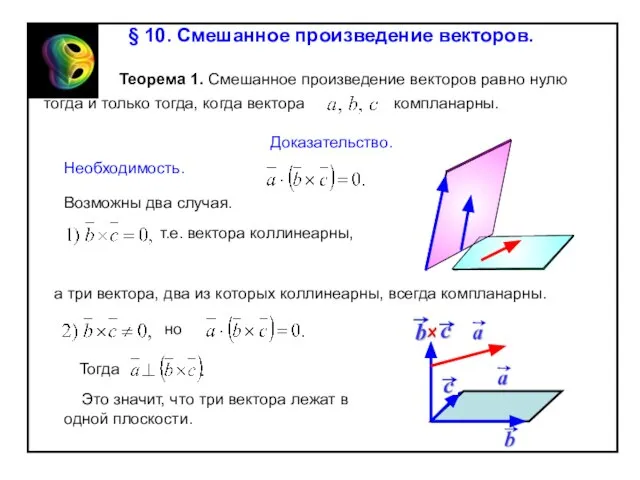
Слайд 65cos
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол
cos
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол
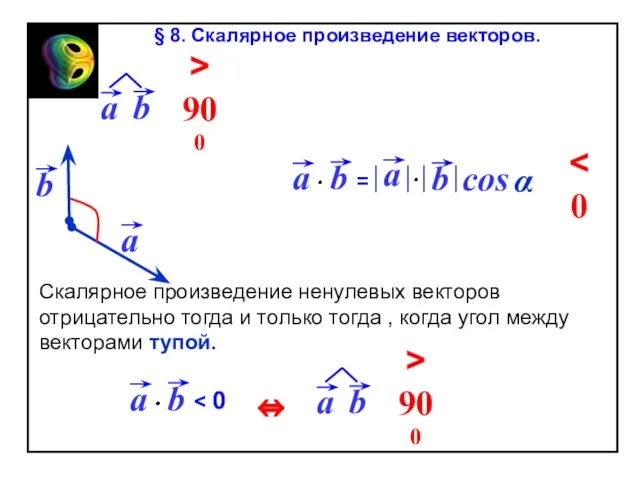
Û
a
< 0
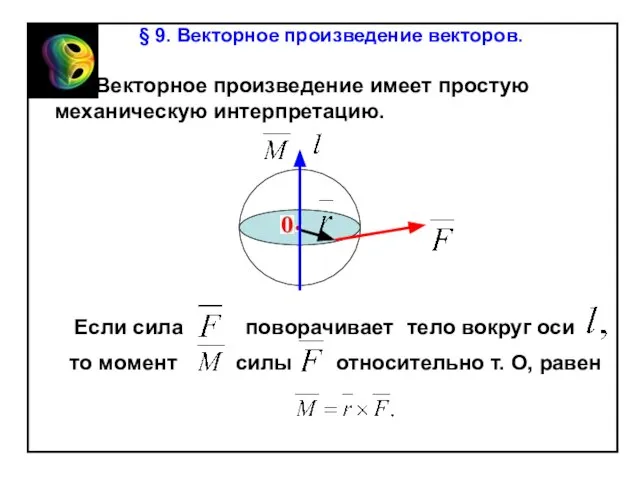
§ 8. Скалярное произведение векторов.
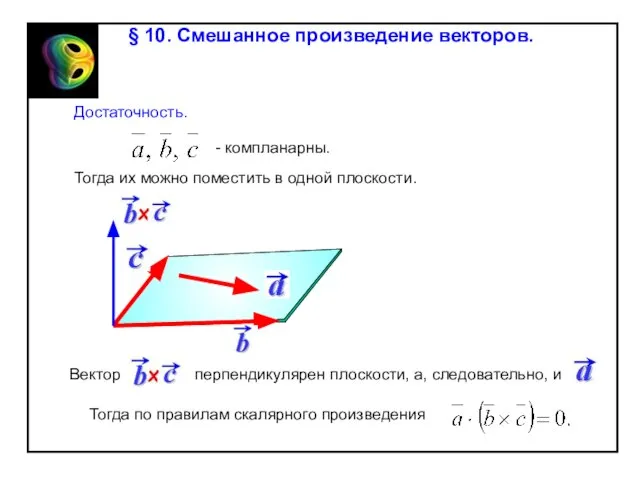
Слайд 66cos 00
cos1800
§ 8. Скалярное произведение векторов.
cos 00
cos1800
§ 8. Скалярное произведение векторов.



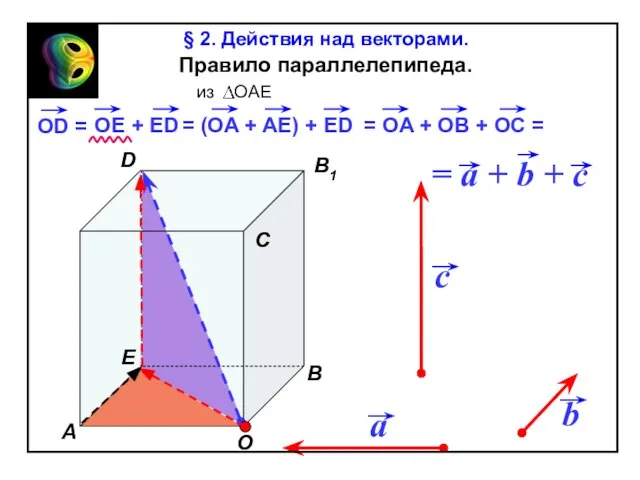
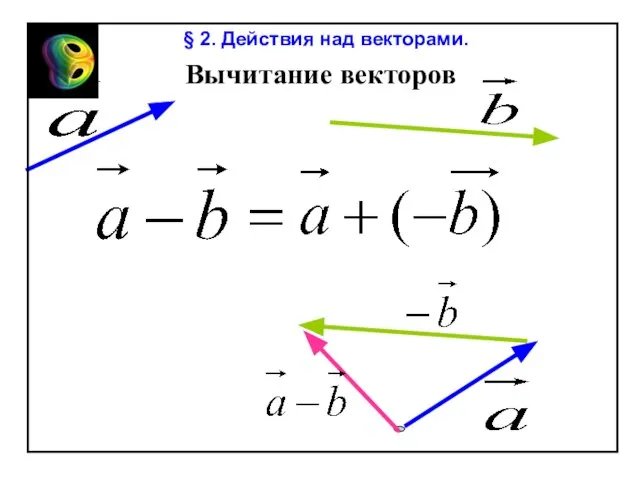
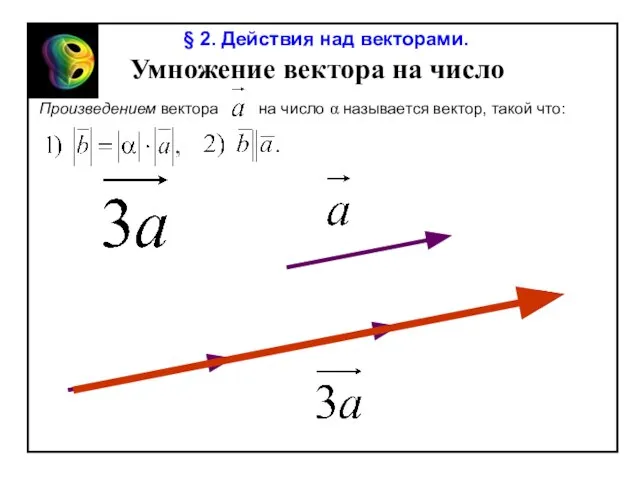

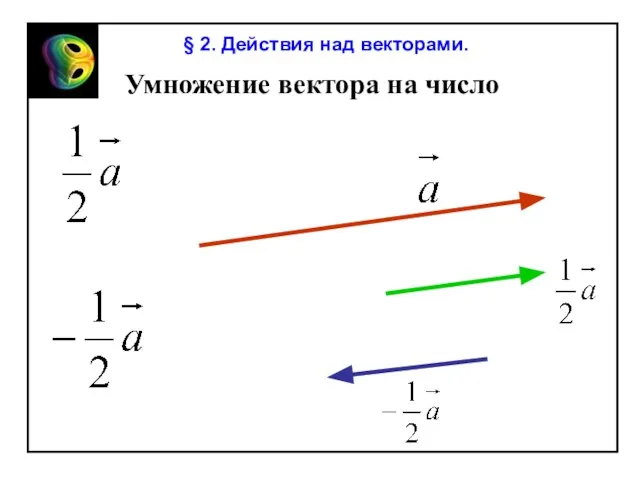















































 Coordinate plane
Coordinate plane Движение в математике
Движение в математике Презентация на тему Приведение дробей к общему знаменателю
Презентация на тему Приведение дробей к общему знаменателю  Множества точек
Множества точек Корреляционный и спектральный анализ случайных процессов
Корреляционный и спектральный анализ случайных процессов Численное интегрирование. Метод средних прямоугольников
Численное интегрирование. Метод средних прямоугольников Сечение поверхности плоскостью
Сечение поверхности плоскостью Логарифмические неравенства
Логарифмические неравенства Треугольник
Треугольник Вписанные и описанные окружности
Вписанные и описанные окружности Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Многомерные случайные величины
Многомерные случайные величины Многоугольники
Многоугольники СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ Счёт до 9. Состав числа 9
Счёт до 9. Состав числа 9 Векторы в пространстве
Векторы в пространстве Урок математики во 2 классе. Повторение
Урок математики во 2 классе. Повторение Заниматика. Миром управляют числа
Заниматика. Миром управляют числа ДПА 11 класс Первообразная и интеграл
ДПА 11 класс Первообразная и интеграл Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат Презентация на тему Математическое моделирование и проектирование
Презентация на тему Математическое моделирование и проектирование  Тригонометрически уравнения
Тригонометрически уравнения Элементы комбинаторики
Элементы комбинаторики Сравни площади фигур на глаз
Сравни площади фигур на глаз Классическое определение вероятности
Классическое определение вероятности Презентация на тему Геометрия в музыке 11 класс
Презентация на тему Геометрия в музыке 11 класс  Презентация на тему Угол между прямыми
Презентация на тему Угол между прямыми  Чертёж призмы
Чертёж призмы