Содержание
- 2. ℕ, ℤ, ℚ, ‖, ℝ _ _
- 4. ℕ, ℤ, ℚ, ‖, ℝ _ _
- 5. Что такое число?
- 8. 2 + 3 = 5
- 9. 2 + 3 = 5
- 10. 2 + 3 = 5
- 11. 1
- 12. «Ку» деревьев «Ололо» собак
- 13. | | | Число
- 14. ℕ = 1, 2, 3 …
- 17. Хватит решать это в натуральных числах!!!
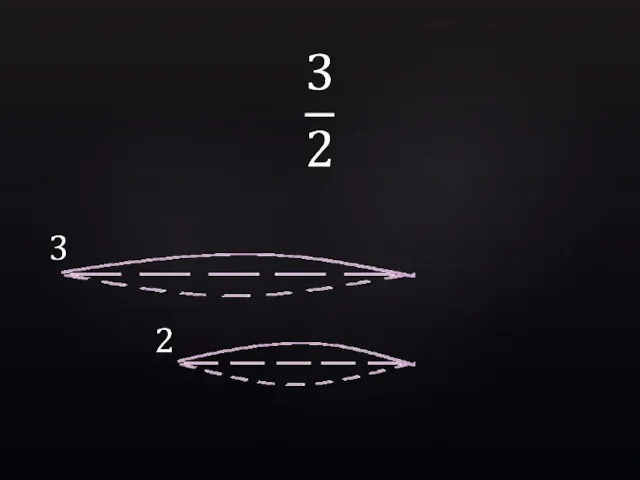
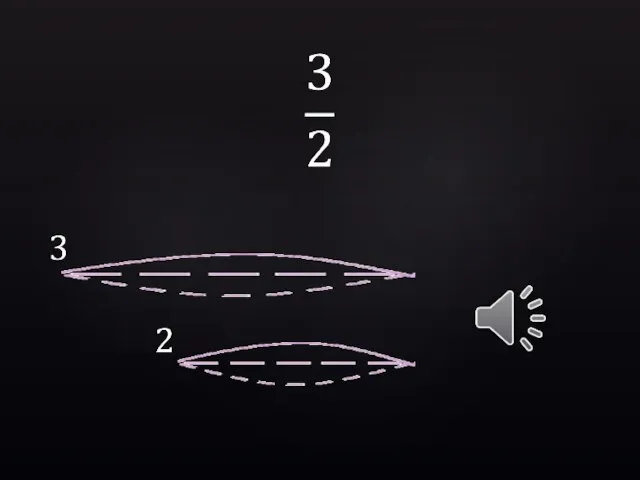
- 20. 1 1 ?
- 27. Φ = 1,618033988749894…
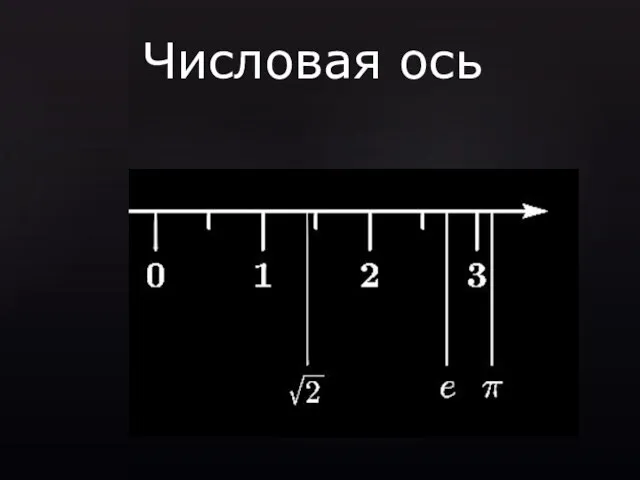
- 28. Числовая ось
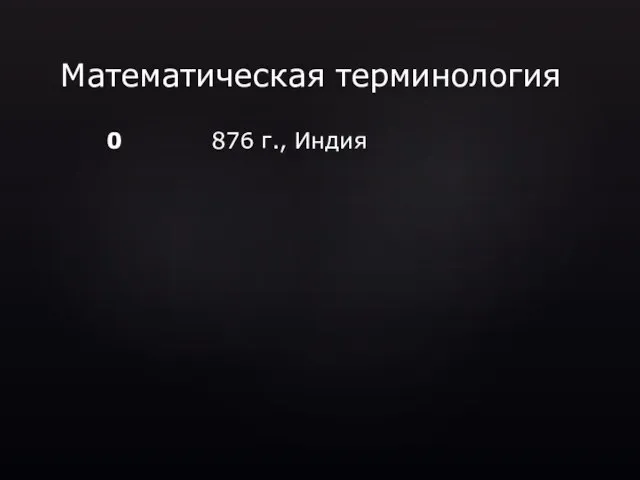
- 29. Математическая терминология 0
- 30. Математическая терминология 0 876 г., Индия
- 31. Математическая терминология 0 876 г., Индия + и - 1489 г., И. Видман = 1557 г.,
- 32. Математическая терминология 0 876 г., Индия + и - 1489 г., И. Видман = 1557 г.,
- 33. Для любых целых m и n
- 39. ℕ, ℤ, ℚ, ‖, ℝ _ _ 0 1
- 40. Какие бывают числа? Комплексные Кватернионы Диофантовы Простые Совершенные Избыточные Трансцендентные Вычислимые Числа Кэли Числа Ферма Числа
- 42. Скачать презентацию






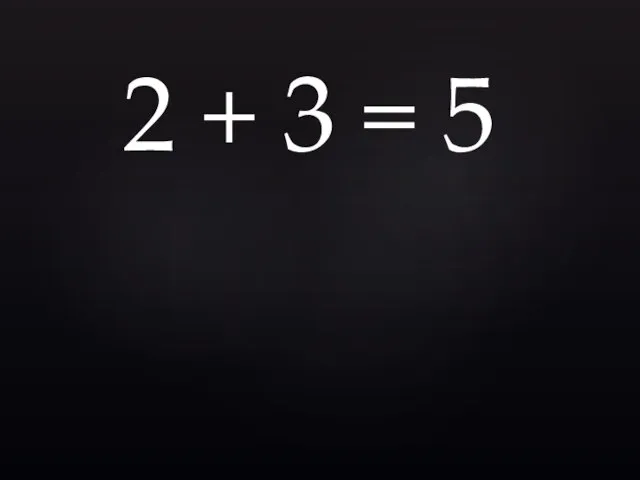
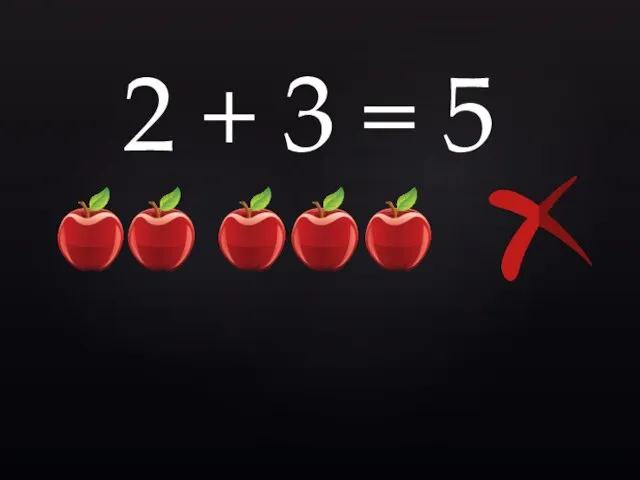
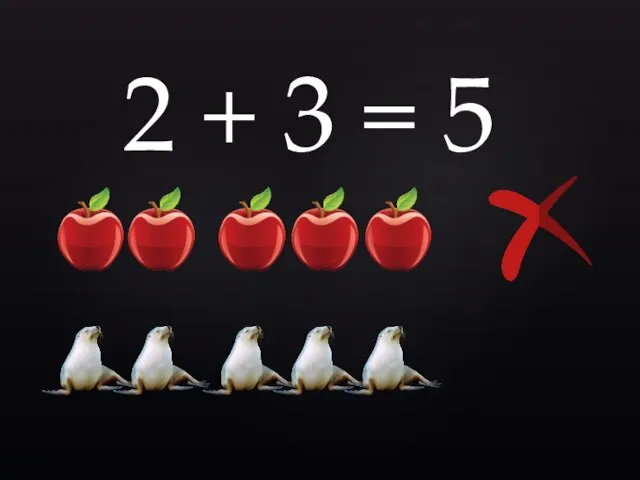



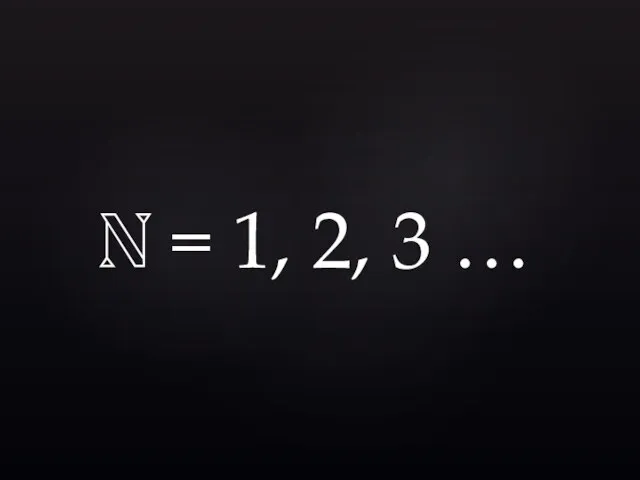







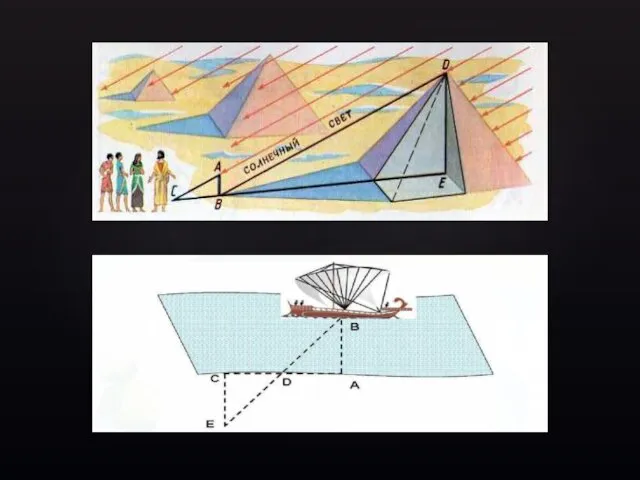
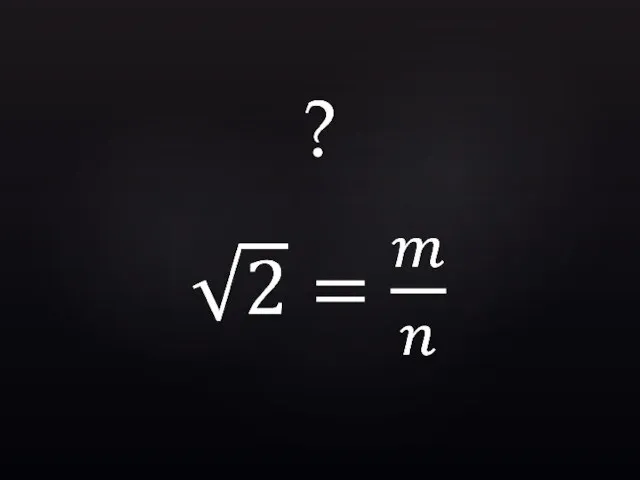

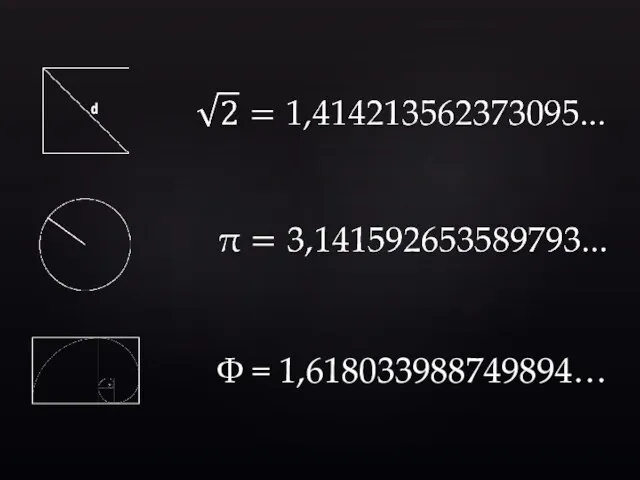




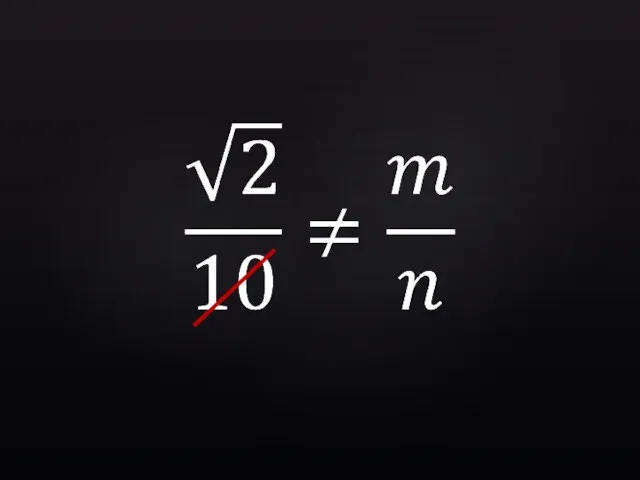
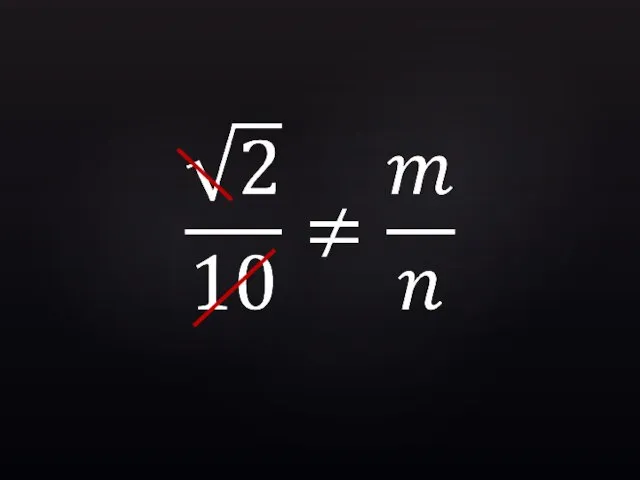
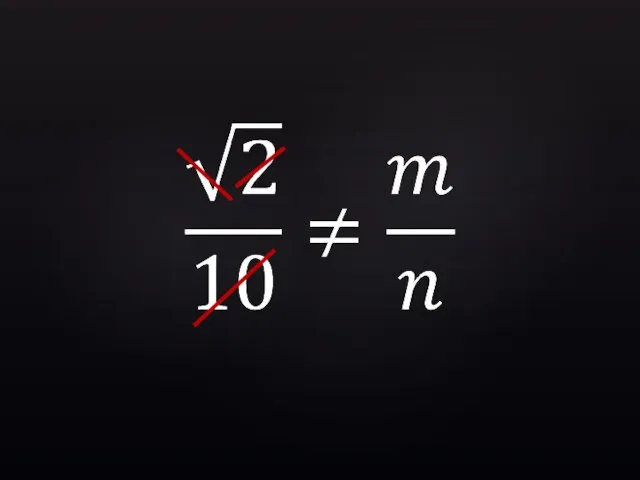
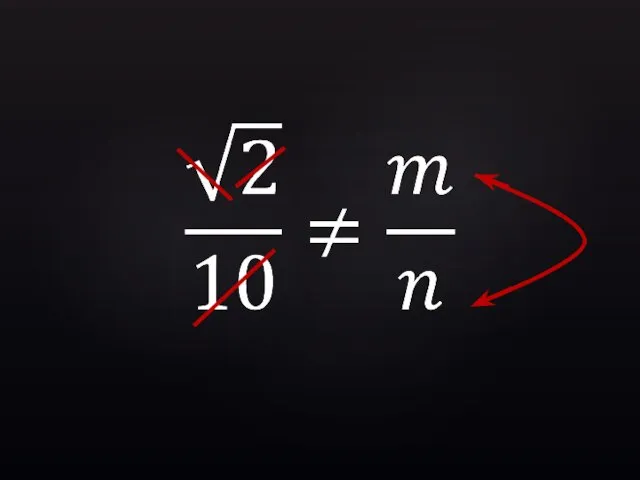
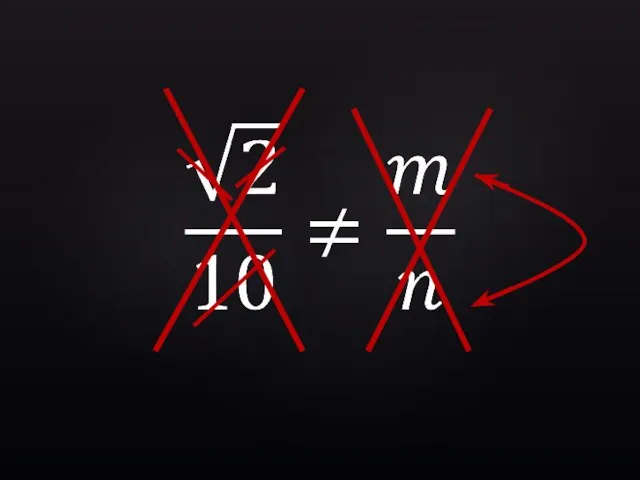


 Аксиомы стереометрии
Аксиомы стереометрии Занимательная математика
Занимательная математика Комплексный анализ. Аналитические функции и конформные отображения
Комплексный анализ. Аналитические функции и конформные отображения Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Задачи по математике. Математический диктант
Задачи по математике. Математический диктант Преобразование логарифмических выражений
Преобразование логарифмических выражений Золотое сечение в архитектуре, скульптуре, живописи
Золотое сечение в архитектуре, скульптуре, живописи Мощность множества
Мощность множества Многонранники в нашей жизни
Многонранники в нашей жизни Можно ли без шаблона разметить круг?
Можно ли без шаблона разметить круг? Построение узла
Построение узла Решение примеров в пределах 10
Решение примеров в пределах 10 Презентация на тему Симметрия относительно прямой
Презентация на тему Симметрия относительно прямой  Математика в литературе
Математика в литературе Критические точки функции
Критические точки функции Математика в медицине
Математика в медицине Аналитическая геометрия в пространстве
Аналитическая геометрия в пространстве Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс) Переместительное свойство умножения
Переместительное свойство умножения Рівняння руху гіроскопу в кардановому підвісі
Рівняння руху гіроскопу в кардановому підвісі Умножение и деление десятичных дробей на двузначное число
Умножение и деление десятичных дробей на двузначное число Понятие логарифма
Понятие логарифма Модели статистического прогнозирования. Урок 31
Модели статистического прогнозирования. Урок 31 Простейшие дифференциальные уравнения 2 порядка
Простейшие дифференциальные уравнения 2 порядка Занимательные математические задания
Занимательные математические задания Свойство дроби. Сравнение обыкновенных дробей
Свойство дроби. Сравнение обыкновенных дробей Решение задач. Самостоятельная работа (ЕГЭ)
Решение задач. Самостоятельная работа (ЕГЭ) Многоугольники в нашей жизни
Многоугольники в нашей жизни