Содержание
- 2. Тригонометрия (греч.) – измерение треугольника Почему в геодезии (и в классической геометрии) большое внимание уделяется измерению
- 3. Наиболее распространены следующие определения синуса и косинуса: По тригонометрическому кругу. Хорошо подходит для определения ограничений и
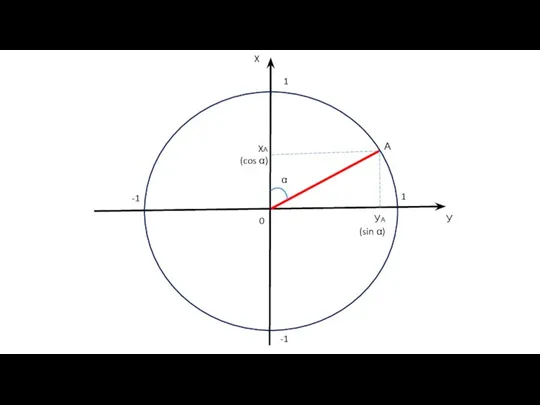
- 4. Тригонометрический круг – это: окружность с центром, совпадающим с началом координат (пересечением осей абсцисс – ОХ
- 5. У X α УА (sin α) XА (cos α) 1 1 -1 -1 0 А
- 6. Таким образом, косинус – проекция на ось ОХ (абсцисс); синус – проекция на ось ОУ (ординат).
- 7. Знаки косинуса и синуса угла в зависимости от четверти (направления движения) X Y I IV III
- 8. Прежде, чем перейти к определениям синуса и косинуса по соотношению длин сторон прямоугольного треугольника, напоминаем, что
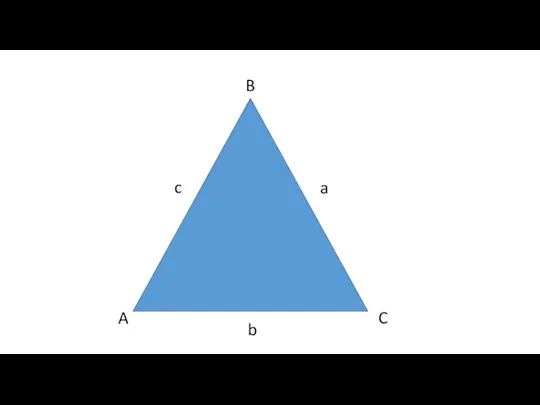
- 9. A B C a b c
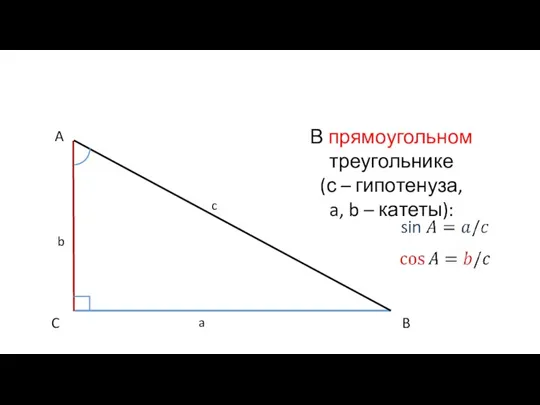
- 10. A B C a b c В прямоугольном треугольнике (с – гипотенуза, a, b – катеты):
- 11. синус угла – это отношение противолежащего катета к гипотенузе; косинус угла – это отношение прилежащего катета
- 12. Определения синуса и косинуса по соотношению катетов и гипотенузы в геодезии и картографии применяют в двух
- 13. 1. Когда проводят работу с прямоугольными системами координат (например, с Декартовой системой, рассматриваемой в курсе «школьной»
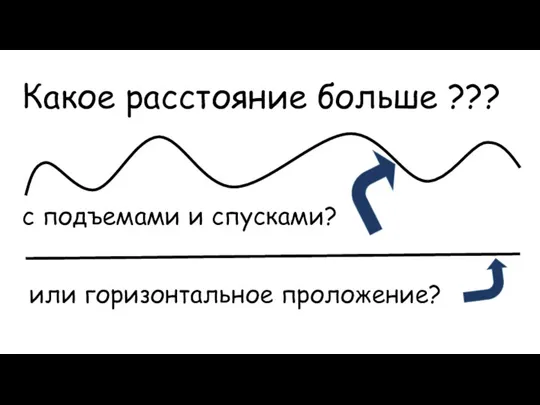
- 14. 2. Когда имеют дело с перпендикулярными проекциями на различные плоскости (например, с горизонтальным проложением). Так, расстояния
- 15. Какое расстояние больше ??? с подъемами и спусками? или горизонтальное проложение?
- 16. Задача 1. Расстояние между пунктами А и В по карте составляет 1800 км, средний подъем трассы
- 18. Скачать презентацию











 Неравенства. Практическая работа №3
Неравенства. Практическая работа №3 Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Презентация Понономарев
Презентация Понономарев Задачки от жителей Солнечного города. 1 класс
Задачки от жителей Солнечного города. 1 класс Простые и составные числа
Простые и составные числа Умножение обыкновенных дробей
Умножение обыкновенных дробей Решение треугольников
Решение треугольников Кенгуру – математика для всех
Кенгуру – математика для всех Основные законы распределения непрерывных случайных величин
Основные законы распределения непрерывных случайных величин Перпендикулярные прямые
Перпендикулярные прямые Справочник по геометрии
Справочник по геометрии Геометрический смысл производной. Производная и её геометрический смысл
Геометрический смысл производной. Производная и её геометрический смысл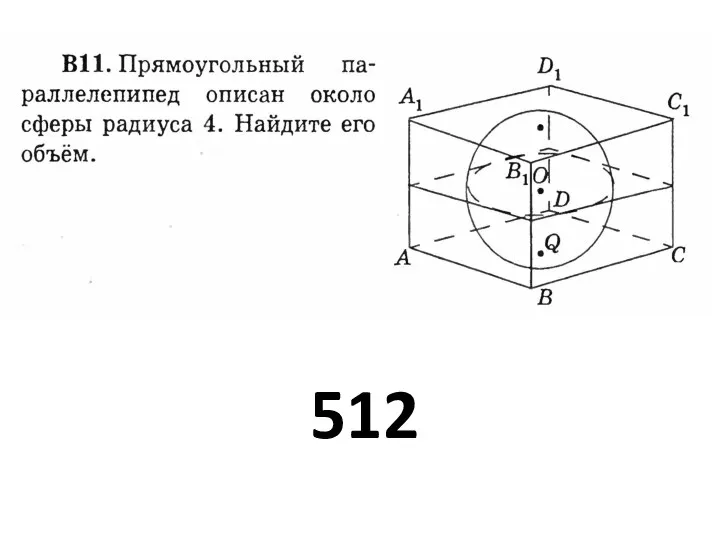 Решение задач по геометрии
Решение задач по геометрии Критические точки функции
Критические точки функции Рациональные числа 6 класс - Презентация по математике_
Рациональные числа 6 класс - Презентация по математике_ Регрессионный анализ
Регрессионный анализ Призма. Площадь полной поверхности прямой призмы
Призма. Площадь полной поверхности прямой призмы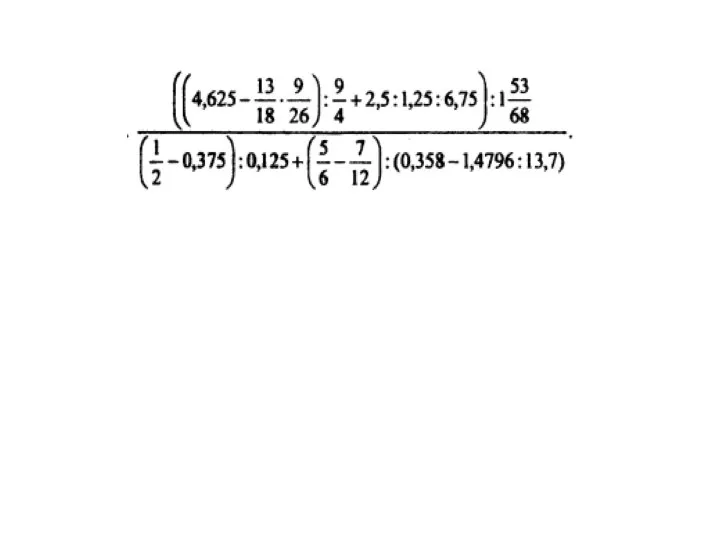 Тождественное преобразование алгебраических выражений. Продолжение
Тождественное преобразование алгебраических выражений. Продолжение Золотое сечение - красота и гармония в математических расчетах
Золотое сечение - красота и гармония в математических расчетах Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ  Презентация на тему ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЧАСОВ
Презентация на тему ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЧАСОВ  Математика в медицине
Математика в медицине Пропорция
Пропорция Интеграл. Первообразная
Интеграл. Первообразная Единицы объёма. Задания
Единицы объёма. Задания Среднее арифметическое. Задания
Среднее арифметическое. Задания Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, сводящиеся к квадратным Математика. Вычитание
Математика. Вычитание