Слайд 4Метод перебора
Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных

таблиц и схем.
Способ перебора может применяться в простых задачах, например в таких, как эта:
Задача 1. Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?
Двузначные числа состоят из двух цифр. Будем помещать по очереди каждую цифру на первую позицию в роли десятков, а потом все цифры переберём в качестве единиц:
11, 12, 13, 14, 15,
21, 22, 23, 24, 25,
31, 32, 33, 34, 35,
41, 42, 43, 44, 45,
51, 52, 53, 54, 55
Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.




 Степень с натуральным показателем
Степень с натуральным показателем Применение производной. Задание 8 (профильный уровень)
Применение производной. Задание 8 (профильный уровень) Использование приема классификации в процессе развития мышления учащихся
Использование приема классификации в процессе развития мышления учащихся Математическое ралли. Итоговое повторение 5 класс
Математическое ралли. Итоговое повторение 5 класс Численное решение алгебраических и трансцендентных уравнений
Численное решение алгебраических и трансцендентных уравнений Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Действия с дробями. Устная работа
Действия с дробями. Устная работа Функция и график
Функция и график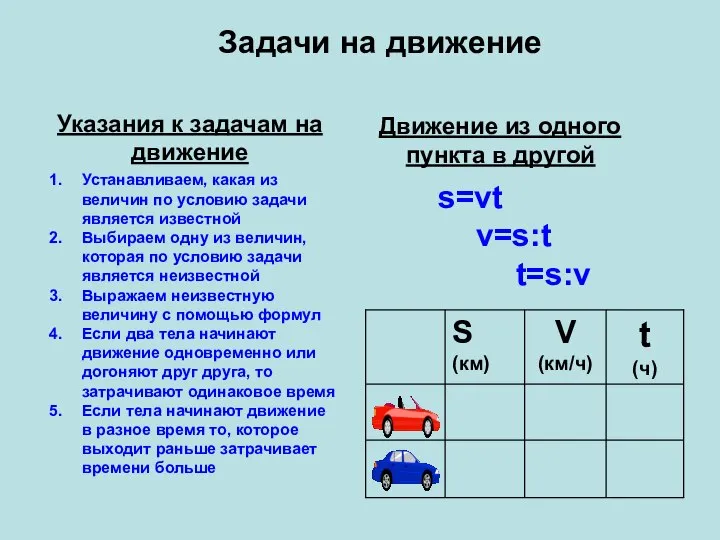 Задачи на движение Указания к задачам на движение
Задачи на движение Указания к задачам на движение Способ группировки
Способ группировки Уравнение окружности и прямой
Уравнение окружности и прямой Обобщение. Высказывания. Ориентирование на местности
Обобщение. Высказывания. Ориентирование на местности Объем шара
Объем шара Своя игра. Вычисление корней
Своя игра. Вычисление корней Презентация на тему Параллельные прямые в пространстве
Презентация на тему Параллельные прямые в пространстве  Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Станция Геометрическая. По тропинкам занимательной математики
Станция Геометрическая. По тропинкам занимательной математики Арксинус. Решение уравнения sin t = a. 10 класс
Арксинус. Решение уравнения sin t = a. 10 класс Вычисление длины дуги
Вычисление длины дуги Логарифмические уравнения
Логарифмические уравнения Презентация на тему Площадь прямоугольника: практикум
Презентация на тему Площадь прямоугольника: практикум  ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ»
ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ» Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Интересные факты про математику
Интересные факты про математику Презентация на тему Геометрические построения с помощью циркуля и линейки
Презентация на тему Геометрические построения с помощью циркуля и линейки  Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Одночлен и его стандартный вид
Одночлен и его стандартный вид Состав числа (домики)
Состав числа (домики)