- Главная
- Математика
- Касательная к окружности

Содержание
Слайд 2Пусть d – расстояние от центра O до прямой KM. Тогда
Касательная к
Пусть d – расстояние от центра O до прямой KM. Тогда
Касательная к

окружности
Свойство касательной. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Признак касательной. Прямая, проходящая через точку окружности и перпендикулярная к радиусу, проведенному в эту точку, является касательной.
KM – касательная ⇔ d = R.
Свойство + признак: если K – точка окружности, то KM – касательная ⇔ KM ⊥ OK.
Доказательство
K
M
d
d = R
Но R = OK, а d = OK ⇔ OK ⊥ KM, ч.т.д.
Слайд 3Касательная к окружности
O
A
K
M
Отрезки касательных, проведенные к окружности из одной точки, равны
Касательная к окружности
O
A
K
M
Отрезки касательных, проведенные к окружности из одной точки, равны
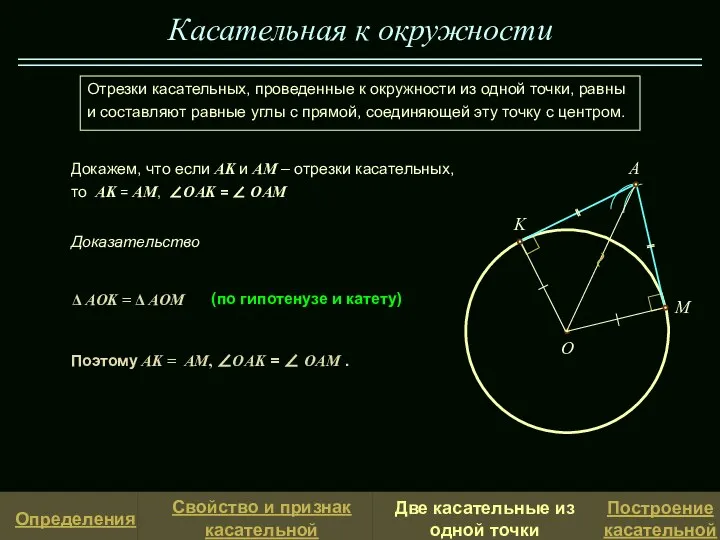
и составляют равные углы с прямой, соединяющей эту точку с центром.
Доказательство
~
Δ AOK = Δ AOM
Поэтому AK = AM, ∠OAK = ∠ OAM .
Докажем, что если AK и AM – отрезки касательных, то AK = AM, ∠OAK = ∠ OAM
(по гипотенузе и катету)
- Предыдущая
Роль жиров в жизни человекаСледующая -
Анализ художественного произведения Исследование транспортной задачи с нечёткими условиями
Исследование транспортной задачи с нечёткими условиями Точка перегиба
Точка перегиба Умножение дробей
Умножение дробей Решение задач на тему Энергосбережение
Решение задач на тему Энергосбережение Наслідки з аксіом стереометрії
Наслідки з аксіом стереометрії Как лгать при помоощи статистики
Как лгать при помоощи статистики Морской бой
Морской бой Формула Пика
Формула Пика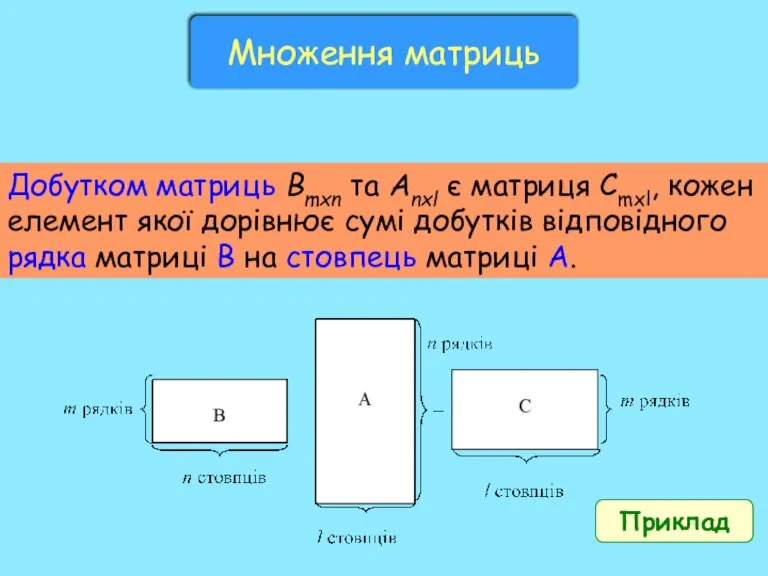 Множення матриць
Множення матриць Теория вероятности
Теория вероятности Единица длины миллиметр
Единица длины миллиметр Презентация на тему Число 8. Цифра 8
Презентация на тему Число 8. Цифра 8  Играем и считаем. Комплекс учебно-развивающих компьютерных игровых тренажеров по начальному обучению математике
Играем и считаем. Комплекс учебно-развивающих компьютерных игровых тренажеров по начальному обучению математике Простейшие функции и их графики
Простейшие функции и их графики Понятие площади и свойства (8 класс)
Понятие площади и свойства (8 класс) СРС 2 ВСК 2. Задачи
СРС 2 ВСК 2. Задачи Внимание: свойства, функции и виды
Внимание: свойства, функции и виды Презентация на тему СОСТАВ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА
Презентация на тему СОСТАВ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА  Математика. Больше Меньше Равно (1 класс )
Математика. Больше Меньше Равно (1 класс ) Математическая игра
Математическая игра Симмертия. Зеркальное отражение – симметрия
Симмертия. Зеркальное отражение – симметрия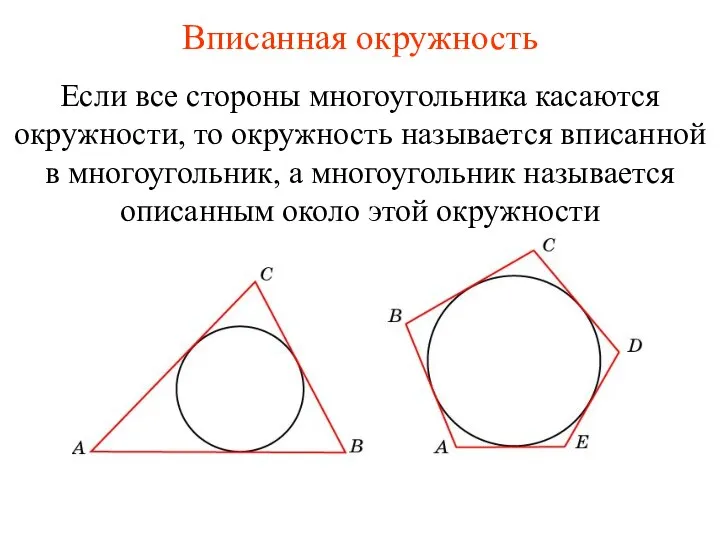 Вписанная окружность
Вписанная окружность Раз, два, три. Спортивно-математический турнир
Раз, два, три. Спортивно-математический турнир Декартовы координаты на плоскости (решение задач)
Декартовы координаты на плоскости (решение задач) Задача о Покупке фруктов
Задача о Покупке фруктов А-11 Триг функции и их свойства 29.09.22 - копия
А-11 Триг функции и их свойства 29.09.22 - копия Параллельность плоскостей (10 класс)
Параллельность плоскостей (10 класс) Презентация на тему Произведение чисел с разными знаками
Презентация на тему Произведение чисел с разными знаками