Слайд 2Докажем, что семейство {Tξ}ξ∈V операторов Дункла является коммутативным относительно композиции.
Теорема 4. Для

произвольных ненулевых векторов ξ, η ∈ V соответствующие операторы Дункла коммутируют:
TξTη = TηTξ.
Доказательство. Рассмотрим разность
Слайд 3которую перепишем в следующем виде:

Слайд 4Очевидно ∂ξ∂η − ∂η∂ξ = 0. Далее, преобразуем выражение
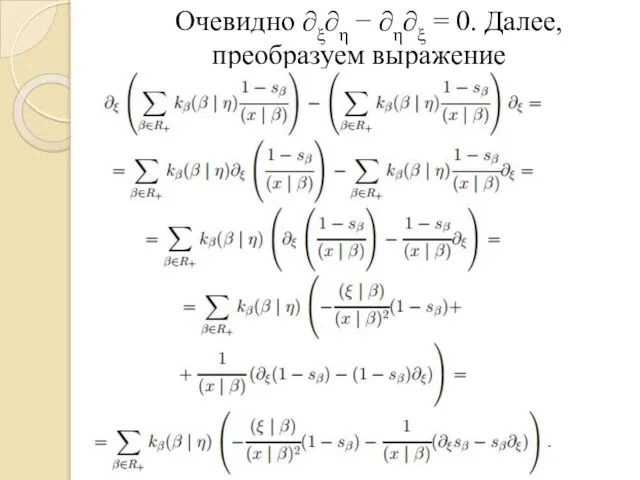
Слайд 5Из эквивариантности оператора ∇ вытекает, что
Поэтому рассматриваемая разность может быть преобразована к

выражению
Слайд 6которое симметрично относительно векторов ξ и η. Но это означает, что к

такому же выражению может быть приведена и разность
Таким образом, получаем следующее соотношение:
Слайд 7Преобразуем правую часть последнего равенства:

Слайд 11Рассмотрим сумму Ω1, которую преобразуем, пользуясь инвариантностью скалярного произведения относительно действия группы

Коксетера.
Получаем
Слайд 12Ясно, что при фиксированном β найдется единственный положительный корень α ′, такой

что sβα = ±α ′. Замечая, что во второй сумме корень sβα находится в числителе и знаменателе, имеем
Слайд 14Заменяя α ′ на α, окончательно получаем, что
Аналогичные рассуждения показывают, что

Слайд 15Меняя в последней сумме α на β и β на α, получаем

Ω1 = Ω2.
Покажем, что Ω3 = 0. В самом деле, меняя во второй сумме α на β и β на α, и пользуясь инвариантностью скалярного произведения, получаем
Слайд 16По тем же причинам, что и выше вместо sαβ можно писать β

′ и считать, что β ′ — положительный корень. И тогда, поскольку sαsβ = ssαβsα,
Слайд 17
Но внутренняя сумма в Ω3 равна нулю в силу леммы 2.1, где

форма
Итак, для произвольных ξ, η
Теорема доказана!


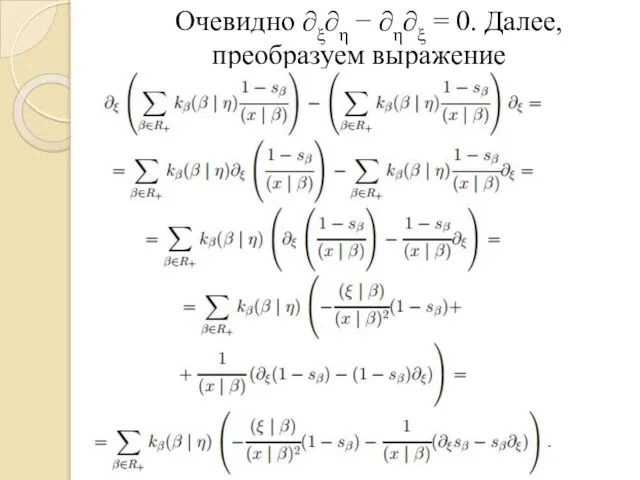



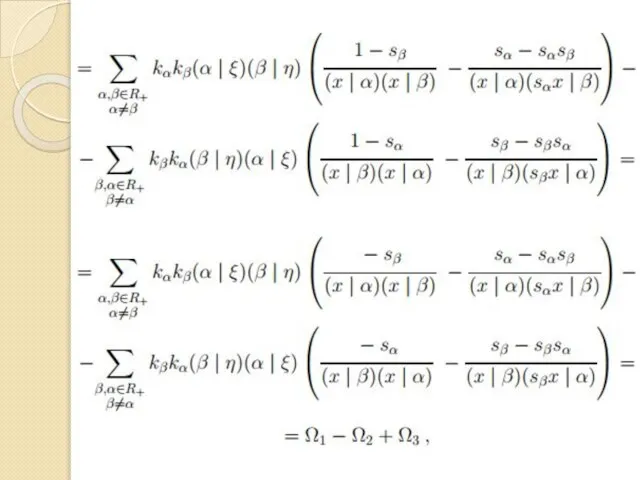








 Понятие числовой последованности
Понятие числовой последованности Действительные числа
Действительные числа Алгебра логики
Алгебра логики Понятие десятичной дроби
Понятие десятичной дроби Алгебраические уравнения
Алгебраические уравнения Глобальная динамическая модель Форрестера
Глобальная динамическая модель Форрестера Практикум по теме х2 = а
Практикум по теме х2 = а Повторение.Геометрия(ЕМН) 10 класс
Повторение.Геометрия(ЕМН) 10 класс Презентация на тему Цифра 3
Презентация на тему Цифра 3 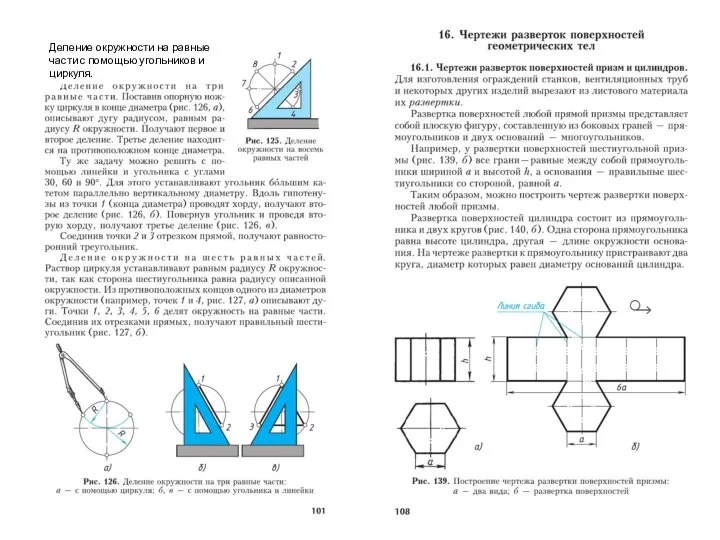 Деление окружности на равные части с помощью угольников и циркуля
Деление окружности на равные части с помощью угольников и циркуля Определители второго и третьего порядка
Определители второго и третьего порядка Решение задач по теме треугольники
Решение задач по теме треугольники Перестановки. Размещения
Перестановки. Размещения Площади фигур. 8 класс
Площади фигур. 8 класс Аксиомы стереометрии
Аксиомы стереометрии Презентация на тему Итоговый тест по математике для 1 класса
Презентация на тему Итоговый тест по математике для 1 класса  Площадь трапеции
Площадь трапеции Размерные цепи
Размерные цепи Десятичные дроби по-английски. Бинарный урок
Десятичные дроби по-английски. Бинарный урок Построение угла, равного данному
Построение угла, равного данному Конспект занятия по математике для будущих первоклассников
Конспект занятия по математике для будущих первоклассников Статистическая теория радиотехнических систем. Постановка задач и классификация методов приема сигналов. (Лекция 10)
Статистическая теория радиотехнических систем. Постановка задач и классификация методов приема сигналов. (Лекция 10) Стереометрия. Теория
Стереометрия. Теория Проверь свои знания. Игра для девятиклассников
Проверь свои знания. Игра для девятиклассников Физико-математических КВН
Физико-математических КВН Разные задачи. Урок 140
Разные задачи. Урок 140 Логарифмы и их свойства
Логарифмы и их свойства Сложение смешанных дробей
Сложение смешанных дробей