Содержание
- 2. Димәк теләсә нинди комплекс санга яссы-лыкның бары тик бер генә ноктасы тиңдәш була һәм киресенчә яссылыкның
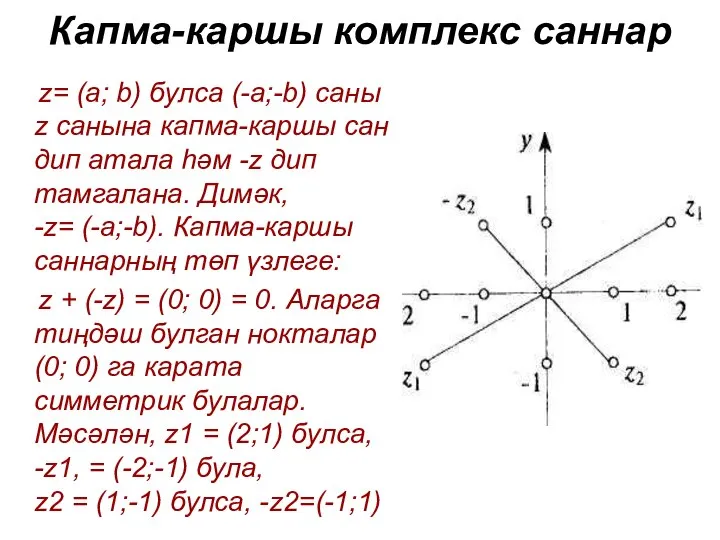
- 3. Капма-каршы комплекс саннар z= (а; b) булса (-а;-b) саны z санына капма-каршы сан дип атала һәм
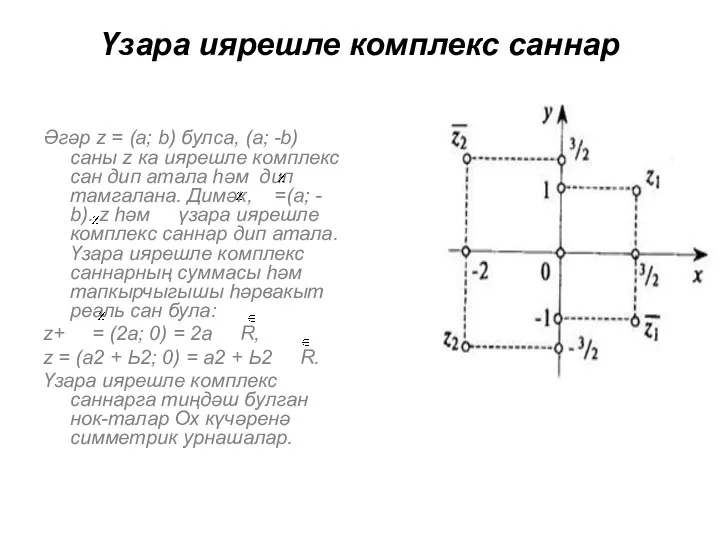
- 4. Үзара иярешле комплекс саннар Әгәр z = (а; b) булса, (а; -b) саны z ка иярешле
- 5. Алгебраик формада бирелгән комплекслы саннарны кушу. z=(a; b) комлекс санын z=a+bi рәве-шендә язу аның алгебраик рәвеше
- 6. Ике комплекс санның аермасын тапканда реаль өлешләр аермасы реаль өлеш, аермасы уйланма өлешләр алдындагы коэффицентлар аермасы
- 7. Комплекс саннарны кушу һәм алуның геометрик мәгънәсе z1= a1 + ib1, z2= a2 + ib2 өчен
- 8. Комплекслы саннарны тапкырлау һәм бүлү Алгебраик формада бирелгән комплекслы саннарны тапкырлауны икебуынны тапкырлау кагыйдәсе буенча башкарырга
- 9. z=(0; 1) уйланма саны уйланма берәмлек дип атала. Ул уйланма берәмлек i дип тамгаланыла. Моңа кадәр
- 10. z3=(-2; -3) Күп вакытта теләсәсә нинди яссылык ноктасын радиус векторлар ярдәмендә күрсәтеп булмаганга теләсә нинди комплекс
- 11. Теләсә нинди реаль сан- уйланма өлеше 0 булган комплекс сан. Әгәр z= (0; b) бирелә, мондый
- 12. Тискәре саннан тамыр алу. Дискриминантты тискәре сан булган квадрат тигезләмәләр чишү. Квадраты -1 гә тигез булган
- 14. Скачать презентацию









 Uravnenia_i_neravenstva_Sistemy_uravneniy
Uravnenia_i_neravenstva_Sistemy_uravneniy Трапеция
Трапеция Турнир имени Лоповка
Турнир имени Лоповка Презентация на тему Подобные треугольники
Презентация на тему Подобные треугольники  График квадратичной функции, содержащей переменную под знаком абсолютной величины
График квадратичной функции, содержащей переменную под знаком абсолютной величины Учебно-методический комплект по математике по ФГОС второй ступени
Учебно-методический комплект по математике по ФГОС второй ступени Введение в геометрию
Введение в геометрию Треугольник паскаля
Треугольник паскаля Пперпендикулярные прямые
Пперпендикулярные прямые Начертательная геометрия – это не просто, это очень просто
Начертательная геометрия – это не просто, это очень просто Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс
Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Тела и поверхности вращения
Тела и поверхности вращения Интерактивная игра-тренажёр. Сколько? Соотношение числа и цифры
Интерактивная игра-тренажёр. Сколько? Соотношение числа и цифры Вписанные и описанные четырехугольники
Вписанные и описанные четырехугольники Дифференциальные уравнения
Дифференциальные уравнения Понятие функции, предел
Понятие функции, предел Движения. 9-й класс
Движения. 9-й класс Окружность и круг. Задачи
Окружность и круг. Задачи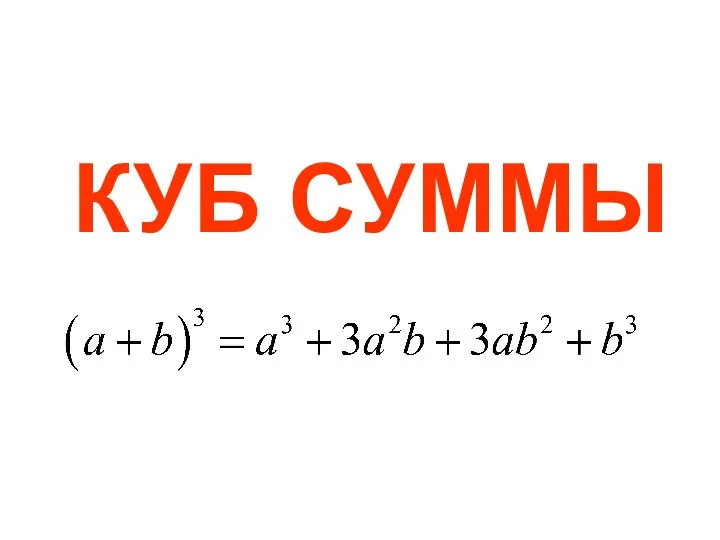 Куб суммы
Куб суммы Презентация на тему Комбинаторные задачи: размещения
Презентация на тему Комбинаторные задачи: размещения  Схемы к задачам
Схемы к задачам Функция у-сосх, её свойства и график
Функция у-сосх, её свойства и график Простейшие тригонометрические уравнения. Задания для устного счета
Простейшие тригонометрические уравнения. Задания для устного счета Отображения (функции)
Отображения (функции) Различные виды тестирования при изучении темы Десятичные дроби
Различные виды тестирования при изучении темы Десятичные дроби Логарифмы вокруг нас
Логарифмы вокруг нас Прикладная математика. Системы уравнений
Прикладная математика. Системы уравнений