Теорія множин. Відношення

Під множиною розуміють деяку сукупність різних поміж собою об’єктів, які добре розпізнаються нашою думкою або інтуїцією і розглядаються як єдине ціле.
Об’єкти, з яких складено множину, називають її елементами. Множини позначаються великими літерами латинської абетки: A, B , C,…, а об’єкти або елементи, які становлять множину, позначаються малими латинськими літерами: a, b, с, ..., або малими латинськими літерами з індексами
Твердження, що множина А складається з елементів a1,, a2, …, an, умовно записується як А = {a1,, a2, …, an}
Потужність множини, або кардинальне число множини, — характеристика множин (у тому числі нескінченних), що узагальнює поняття кількості (числа) елементів скінченної множини.
Порядок елементів множини не має значення.
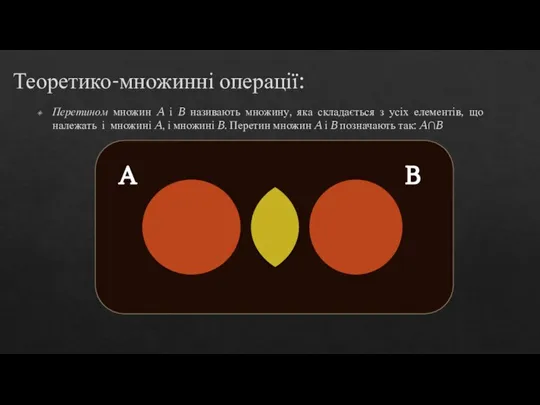
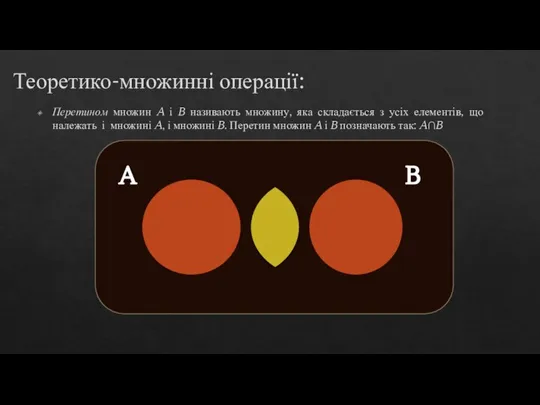
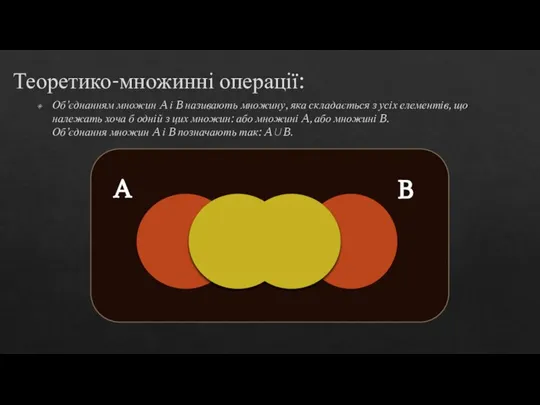
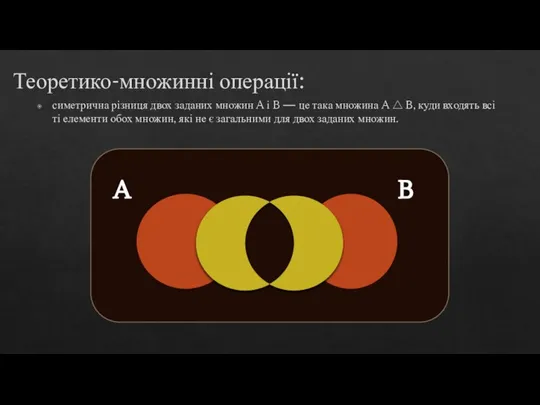
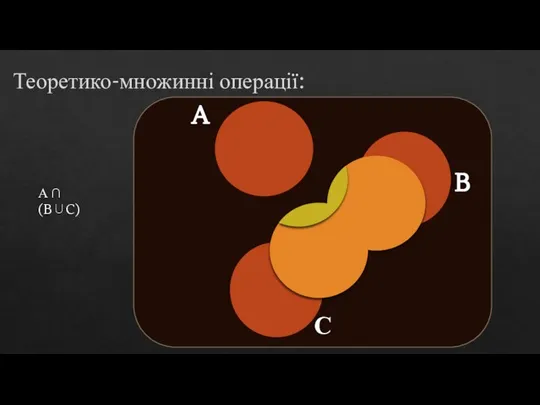
Теорія множин

Способи задання множин:
Множину можна задавати явним переліченням всіх її елементів: А = {a1,, a2, …, an}
За допомогою характеристичних властивостей, які мають всі елементи даної множини. Наприклад, цю ж множину А можна записати так:
За допомогою діаграм Ейлера-Венна:

Теоретико-множинні операції:
Перетином множин A і B називають множину, яка складається з усіх елементів, що належать і множині A, і множині B. Перетин множин A і B позначають так: A∩B
A
B

Теоретико-множинні операції:
Перетином множин A і B називають множину, яка складається з усіх елементів, що належать і множині A, і множині B. Перетин множин A і B позначають так: A∩B
A
B
∩

Теоретико-множинні операції:
Перетином множин A і B називають множину, яка складається з усіх елементів, що належать і множині A, і множині B. Перетин множин A і B позначають так: A∩B
A
B

Теоретико-множинні операції:
Об’єднанням множин A і B називають множину, яка складається з усіх елементів, що належать хоча б одній з цих множин: або множині A, або множині B.
Об’єднання множин A і B позначають так: A∪B.
A
B

Теоретико-множинні операції:
Різницею множин А і В називається множина, яка складаєть­ся з усіх елементів, які належать множині А і не належать мно­жині В.
Різницю A і B позначають так: A∖B.
A
B

Теоретико-множинні операції:
симетрична різниця двох заданих множин A і B — це така множина A △ B, куди входять всі ті елементи обох множин, які не є загальними для двох заданих множин.
A
B

Теоретико-множинні операції:
Якщо всі множини, які ми розглядаємо, є підмножинами якоїсь так званої універсальної множини U, то різниця U \ A називається доповненням множини A. Тобто доповненням множини A називається множина, яка складається з усіх елементів, які не належать множині А (але які належать універсальній множині U). Доповнення множини A позначають так: Ā.
A
Ā
U

Теоретико-множинні операції:
A
B
А ∩ (B∪C)
С

Відношення
Об’єднанням множин A і B називають множину, яка складається з усіх елементів, що належать хоча б одній з цих множин: або множині A, або множині B. Об’єднання множин A і B позначають так: A∪B.