HMM выравнивание

X
(+1,+0)
M
(+1,+1)
Y
(+0,+1)
-e
-d
-d
-e
s(xi,yj)
s(xi,yj)
s(xi,yj)
X
qxi
M
pxiyj
Y
qyj
ε
ε
1-ε
1-ε
δ
δ
1-δ
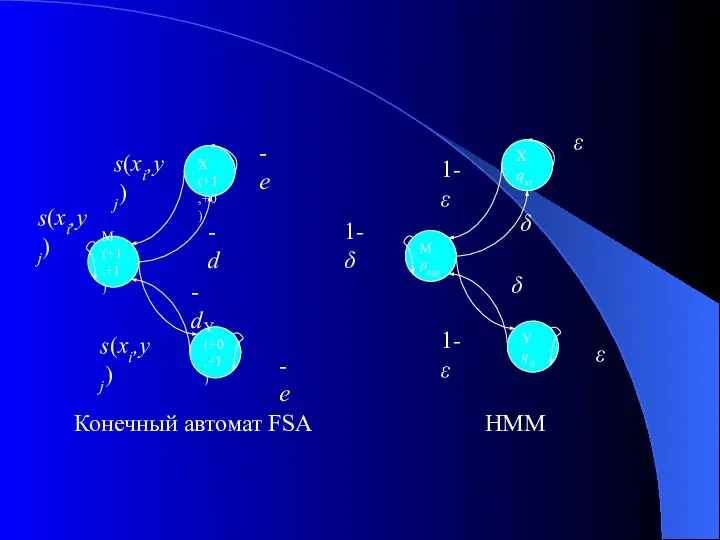
Конечный автомат FSA
HMM

Рекурсия FSA

X
qxi
M
pxiyj
Y
qyj
ε
ε
1-ε-τ
δ
δ
1-2δ-τ
1-ε-τ
δ
δ
τ
τ
τ
τ
Begin
End
1-2δ-τ

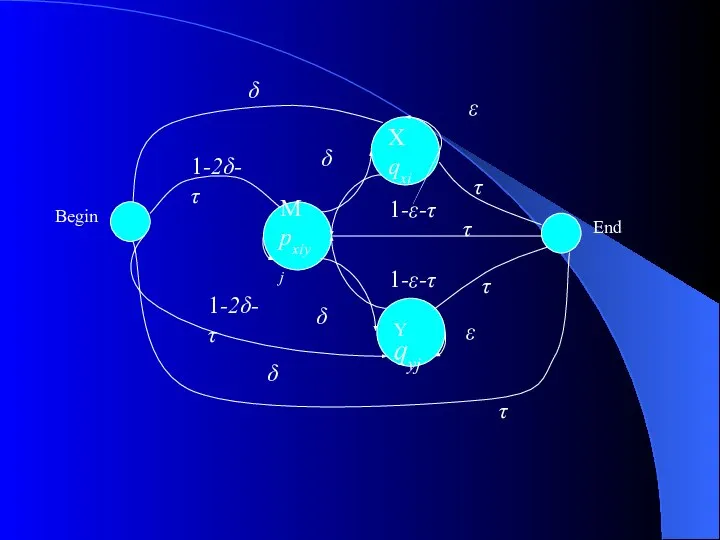
Алгоритм Витерби
Начало:
vM(0, 0) = 1. vX(0, 0) = vY(0, 0) = 0 v*(-1, j) = v*(i, -1) = 0.
Рекурсия: i = 0,…,n, j = 0,…,m, except for(0,0);
Вывод:

Полная вероятность выравниваний
Алгоритм: Forward для парных HMMs
Начало:
fM(0, 0) = 1, fX(0,0) = fY(0,0)= 0.
All f•(i,-1), f•(-1, j) are set to 0.
Рекурсия: i = 0,…,n, j = 0,…,m except (0,0);
Вывод:

Вероятность выровненных xi и yj
Forward algorithm
Backward algorithm
Forward algorithm