Содержание
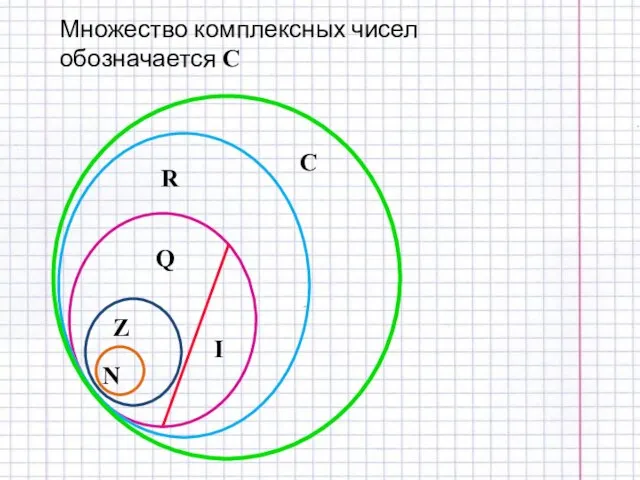
- 2. Множество комплексных чисел обозначается С N Z Q I R C
- 3. Термин “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777
- 4. Н. Н. Богомолов и В. С. Владимиров - к проблемам квантовой теории поля. Большой вклад в
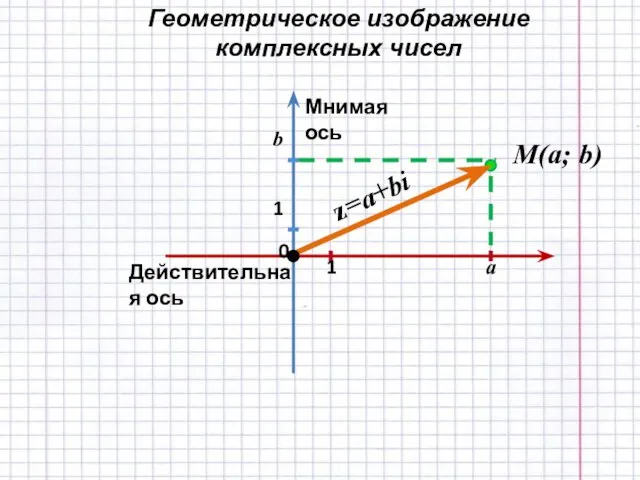
- 5. Обозначение: алгебраическая форма записи комплексного числа
- 6. a - действительная часть комплексного числа z. Обозначается a=Re z. b -мнимая часть комплексного числа z.
- 7. Мнимая ось Действительная ось 0 1 1 a b M(a; b) z=a+bi Геометрическое изображение комплексных чисел
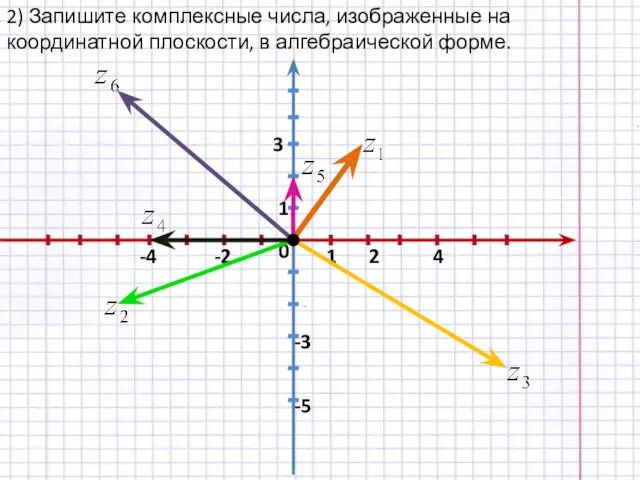
- 8. 2) Запишите комплексные числа, изображенные на координатной плоскости, в алгебраической форме. 0 1 1 -2 4
- 9. Примеры: 1) Изобразите комплексные числа на плоскости
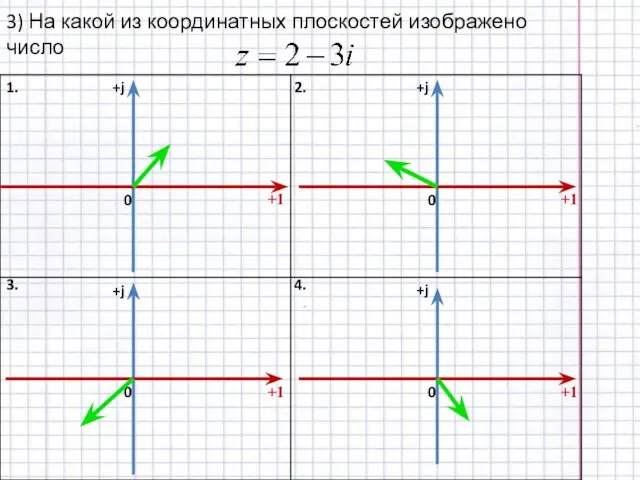
- 10. 3) На какой из координатных плоскостей изображено число +j +1 0 1. 2. 3. 4. +j
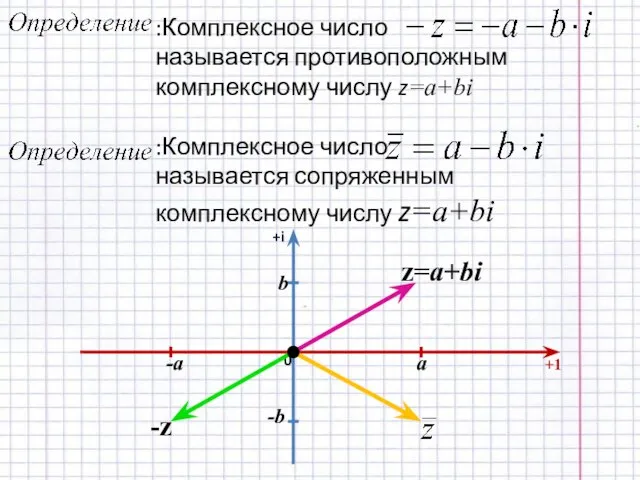
- 11. +i +1 0 z=a+bi -z a -a b -b
- 12. 1. Запишите числа, противоположные и сопряженные данным: 2. Какие из данных чисел являются сопряженным и противоположным
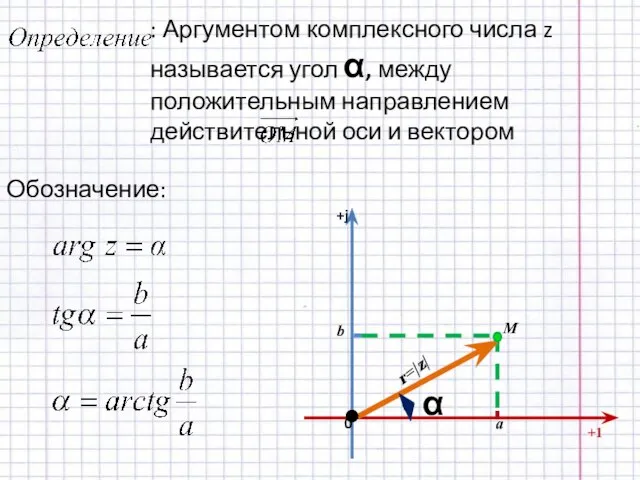
- 13. Модуль и аргумент комплексного числа
- 14. Примеры: Найти модуль комплексных чисел:
- 15. Обозначение: +1 α
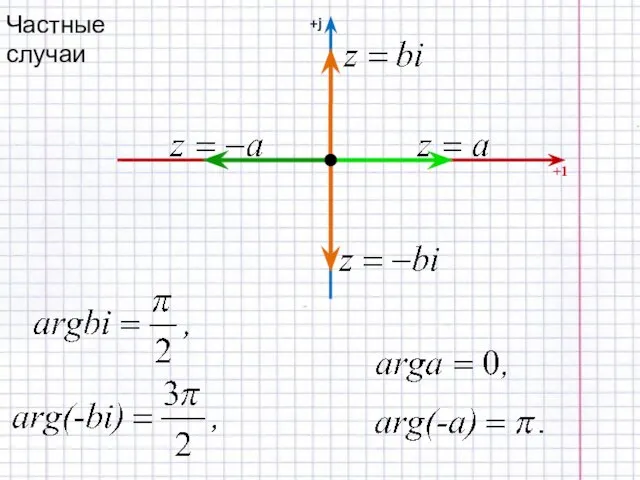
- 16. Частные случаи +1 +j
- 18. Скачать презентацию








 Ракеты и символы
Ракеты и символы Решение задач. Урок 22
Решение задач. Урок 22 1-2_1
1-2_1 Презентация на тему Полупрямая
Презентация на тему Полупрямая  Признаки подобия треугольников (урок-практикум)
Признаки подобия треугольников (урок-практикум) Проценты. Устный математический диктант
Проценты. Устный математический диктант Треугольники. Часть 1
Треугольники. Часть 1 Площади многогранников
Площади многогранников Задачи практического характера в разных областях науки и техники
Задачи практического характера в разных областях науки и техники Решение заданий с производной
Решение заданий с производной Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Иррациональные неравенства
Иррациональные неравенства Метод наименьших квадратов. Ordinary Least Squares, OLS
Метод наименьших квадратов. Ordinary Least Squares, OLS Объём параллелепипеда. Задачи
Объём параллелепипеда. Задачи Взаимно обратные числа
Взаимно обратные числа Тренинг по математике
Тренинг по математике Понятие предела функции
Понятие предела функции Цифры от 0 до 9
Цифры от 0 до 9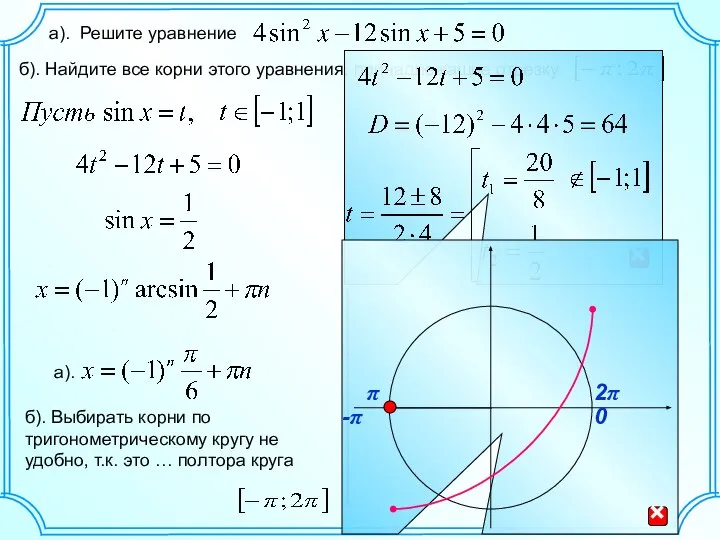 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Прямое сложение и вычитание
Прямое сложение и вычитание Производная сложной функции
Производная сложной функции Деление на двузначное число
Деление на двузначное число Планы второго порядка
Планы второго порядка Свойства бинарных отношений
Свойства бинарных отношений Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Методы решения экстремальных задач
Методы решения экстремальных задач Бинарный урок физики и геометрии
Бинарный урок физики и геометрии