Слайд 2ГЛАС учителя, уставшего от списываний
Работу выполняйте сами!
Жду фото до 14.00

Слайд 3Критерии отметок за работу
Оценка «5»:
Выполнены без ошибок (возможны недочеты 1-2) все задания,

включая выбор верных утверждений.
Оценка «4»:
Выполнены без ошибок (возможны недочеты 1-2) все задания, кроме №3 , включая выбор верных утверждений или не сделан выбор верных утверждений, но все задания выполнены без ошибок.
Оценка «3»:
Выполнены с ошибками – задание с выбором верных утверждений, №1, №2, №4.
В остальных случаях – оценка «2».
Слайд 4Выпишите верные утверждения:
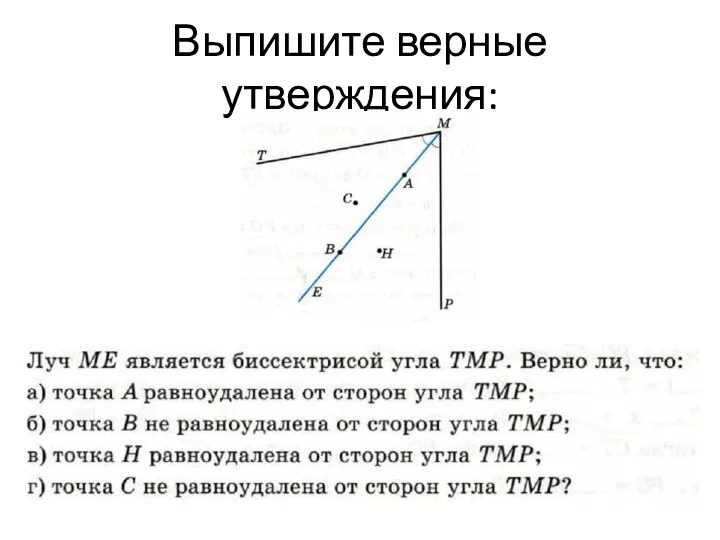
Слайд 5Задача №1
Записать решение в тетрадь, заполнив пропуски
т.е., вычислить НМ

Слайд 6Задача №2
Оформите решение в тетрадь
Стороны угла О касаются каждой из двух
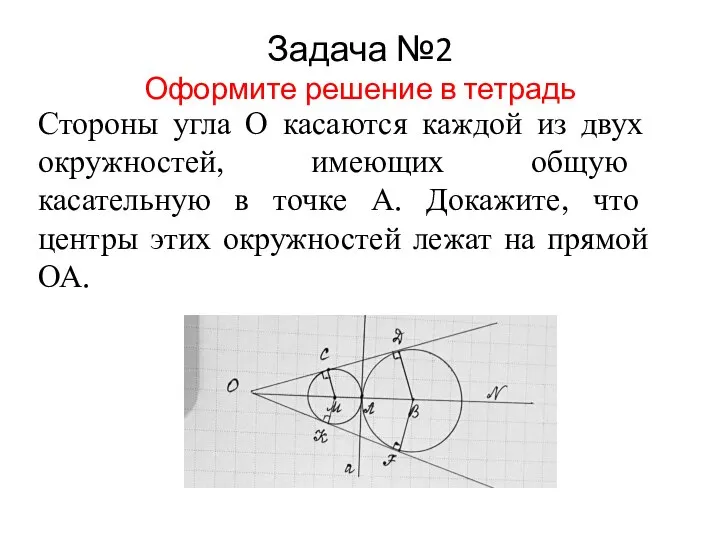
окружностей, имеющих общую касательную в точке А. Докажите, что центры этих окружностей лежат на прямой ОА.
Слайд 7Задача №2
План решения:
Доказать, что М лежит на биссектрисе угла О (смотри теорему

на с.173 часть 1).
Доказать, что В лежит на биссектрисе угла О.
МА ┴ а, ВА ┴ а, поэтому точки М, А и В лежат на одной прямой. Ранее было доказано, что В и М лежат на биссектрисе угла. Следовательно, точки О, М, А, В лежат на одной прямой (биссектрисе угла).
Слайд 8Задача №3
Оформите решение в тетрадь
Стороны угла А касаются окружности с центром О
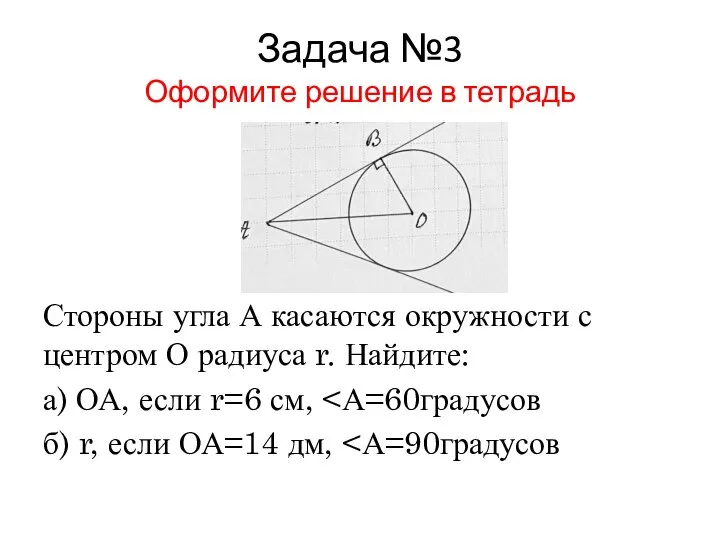
радиуса r. Найдите:
а) ОА, если r=6 см, <А=60градусов
б) r, если ОА=14 дм, <А=90градусов
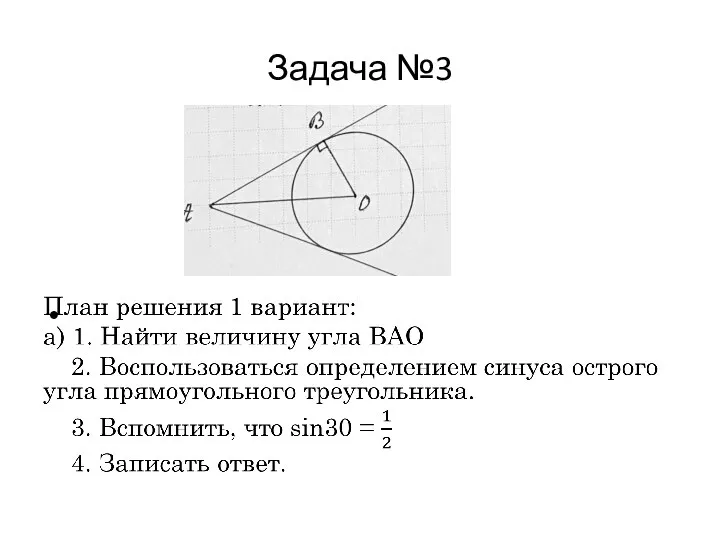
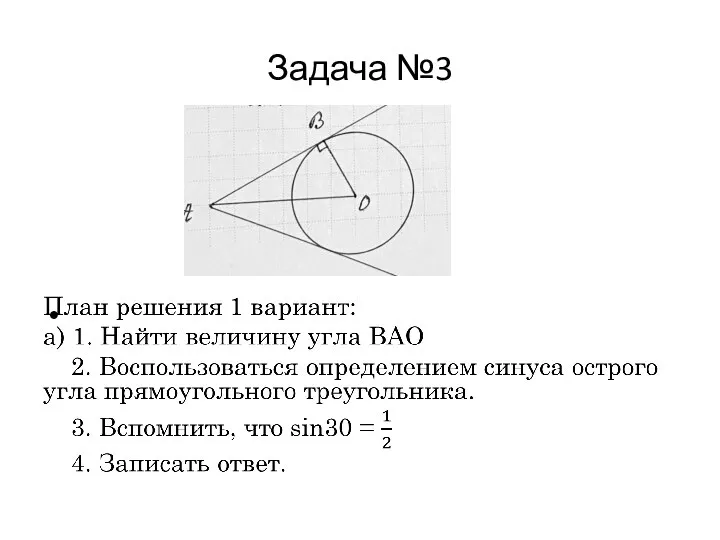
Слайд 11Задача №3
План решения 2 вариант:
б) 1. Найти величину угла ВАО
2. Найти
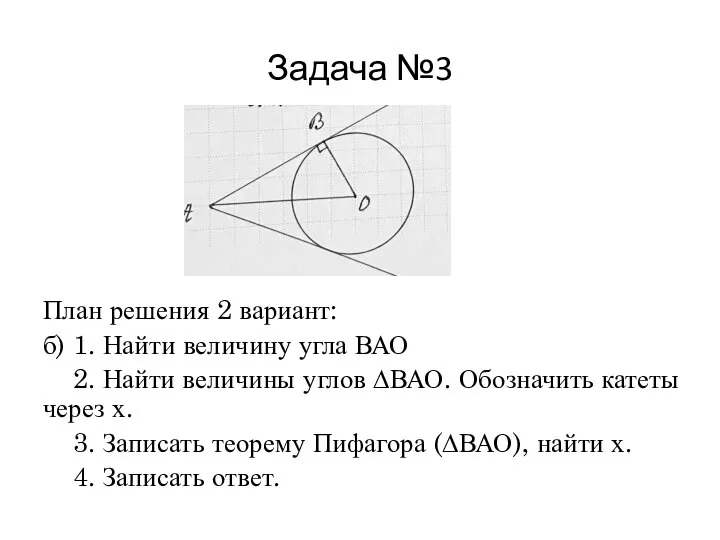
величины углов ∆ВАО. Обозначить катеты через х.
3. Записать теорему Пифагора (∆ВАО), найти х.
4. Записать ответ.
Слайд 12Задача №4
Записать решение в тетрадь, заполнив пропуски










 Неопределенный интеграл
Неопределенный интеграл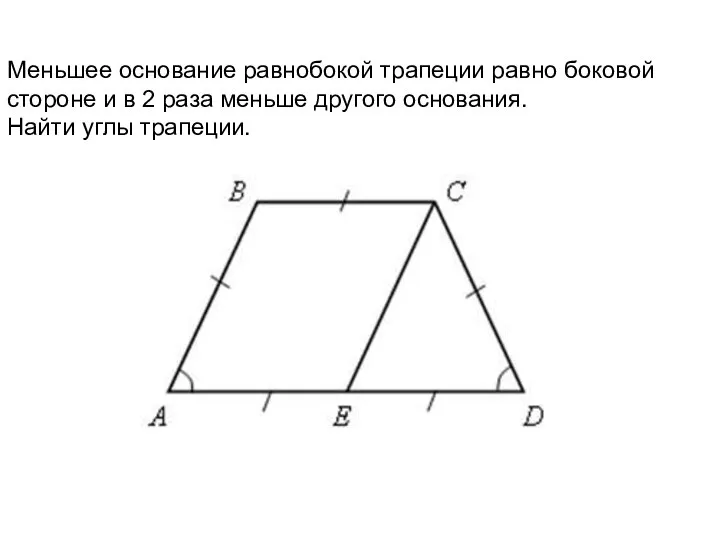 Параллелограмм и трапеция. Урок 8
Параллелограмм и трапеция. Урок 8 Геометрические фигуры
Геометрические фигуры Предел последовательности. Урок 1
Предел последовательности. Урок 1 Презентация на тему Десятичные дроби
Презентация на тему Десятичные дроби  Колесо истории математики
Колесо истории математики Стародубцева Анна 9-а класс
Стародубцева Анна 9-а класс Бой эрудитов
Бой эрудитов Математические ребусы. 4 класс
Математические ребусы. 4 класс Понятие квадратного корня из неотрицательного числа
Понятие квадратного корня из неотрицательного числа Лето в цифрах. Маршрут поездки
Лето в цифрах. Маршрут поездки Разбиение множеств на классы
Разбиение множеств на классы Сложение десятичных дробей
Сложение десятичных дробей Число и цифра 1. 1 класс
Число и цифра 1. 1 класс Урок математики в 4 классе по системе Л.В.Занкова (1-4) «Действия с многозначными числами» Автор: Каграманян Елена Владимировна, учи
Урок математики в 4 классе по системе Л.В.Занкова (1-4) «Действия с многозначными числами» Автор: Каграманян Елена Владимировна, учи Классы интегрируемых функций
Классы интегрируемых функций Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции
Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции Приложения производной
Приложения производной Презентация на тему Свойства функции
Презентация на тему Свойства функции  Волшебная страна - Геометрия. Занятие 3
Волшебная страна - Геометрия. Занятие 3 Тетраэдр
Тетраэдр Линейные рекуррентные соотношения и методы их решения
Линейные рекуррентные соотношения и методы их решения Численное решение алгебраических и трансцендентных уравнений
Численное решение алгебраических и трансцендентных уравнений Десятичные дроби. Выполнить действия
Десятичные дроби. Выполнить действия Презентация на тему Буквенная запись свойств сложения и вычитания (5 класс)
Презентация на тему Буквенная запись свойств сложения и вычитания (5 класс)  Системы принятия решений
Системы принятия решений Корень степени n
Корень степени n Начальные геометрические сведения. Признаки равенства треугольников
Начальные геометрические сведения. Признаки равенства треугольников