Содержание
- 2. Тема Геометрический смысл производной
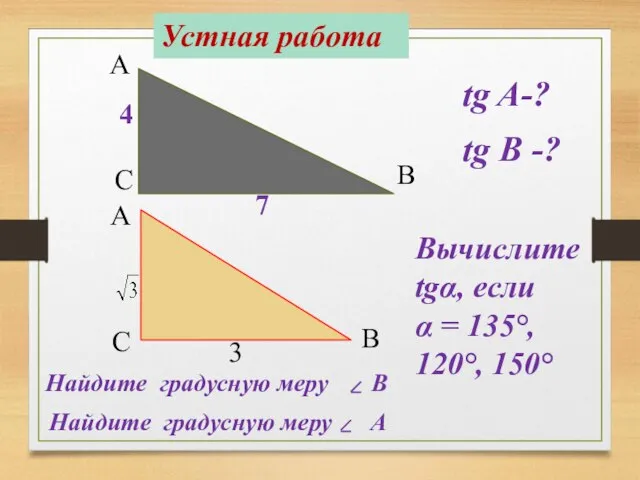
- 3. А С В tg A-? tg В -? 4 7 А В С Найдите градусную меру
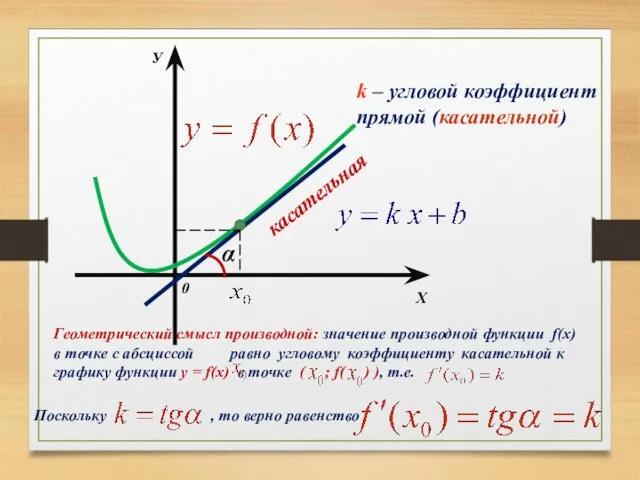
- 4. Х У 0 касательная α k – угловой коэффициент прямой (касательной) Геометрический смысл производной: значение производной
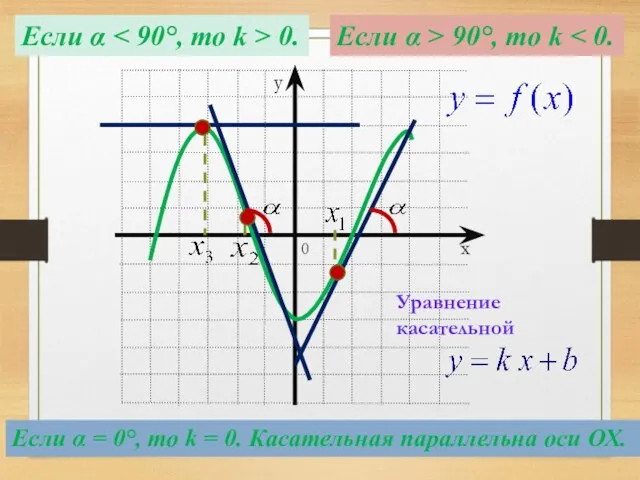
- 5. Если α 0. Если α > 90°, то k Если α = 0°, то k =
- 6. Острый или тупой угол образует касательная к графику функции в точке х₀ с положительной полуосью Ох?
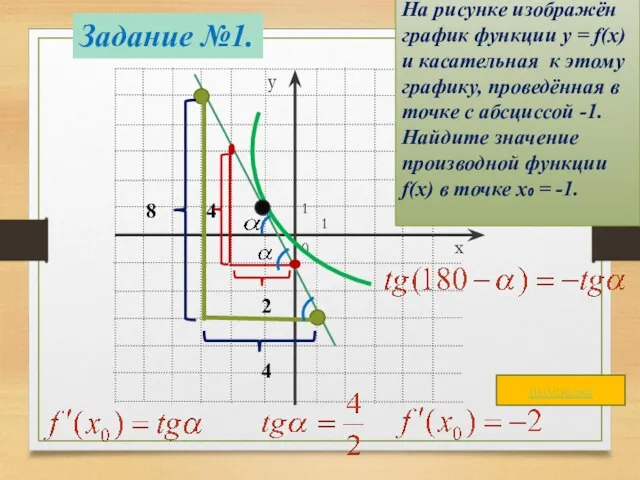
- 7. 1 0 1 4 2 Задание №1. На рисунке изображён график функции y = f(x) и
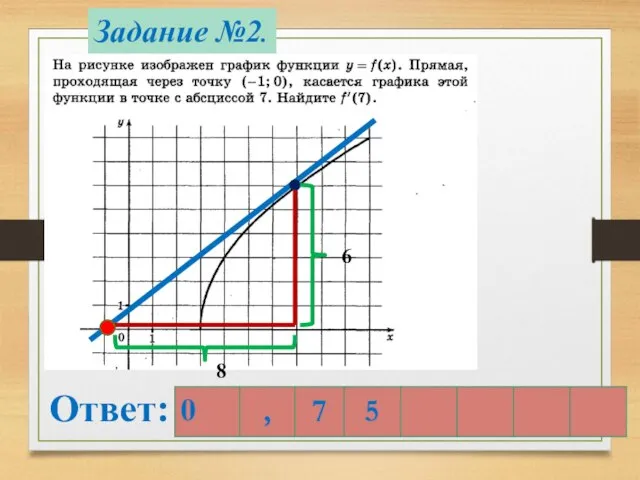
- 8. Задание №2. Ответ: 6 8
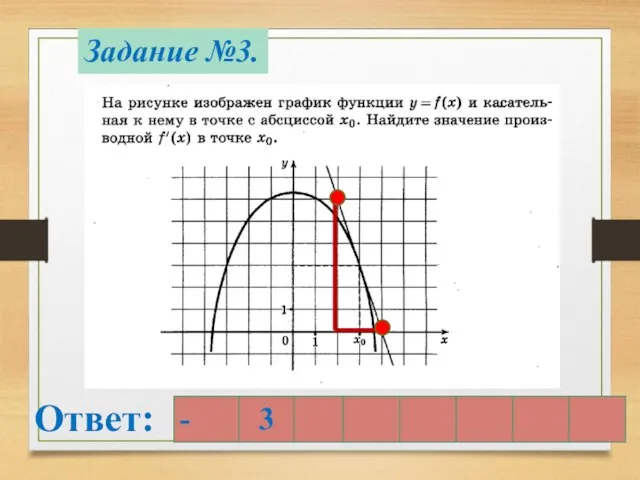
- 9. Задание №3. Ответ:
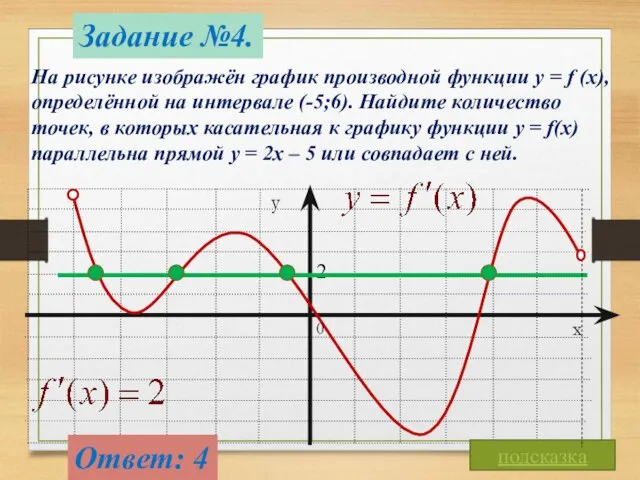
- 10. Задание №4. На рисунке изображён график производной функции y = f (x), определённой на интервале (-5;6).
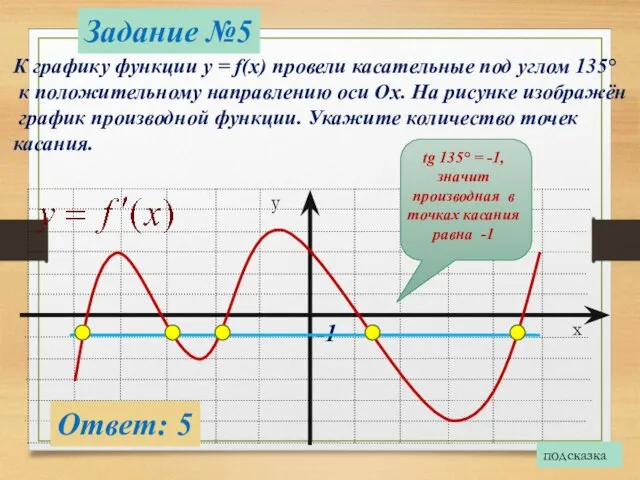
- 11. Задание №5 К графику функции y = f(x) провели касательные под углом 135° к положительному направлению
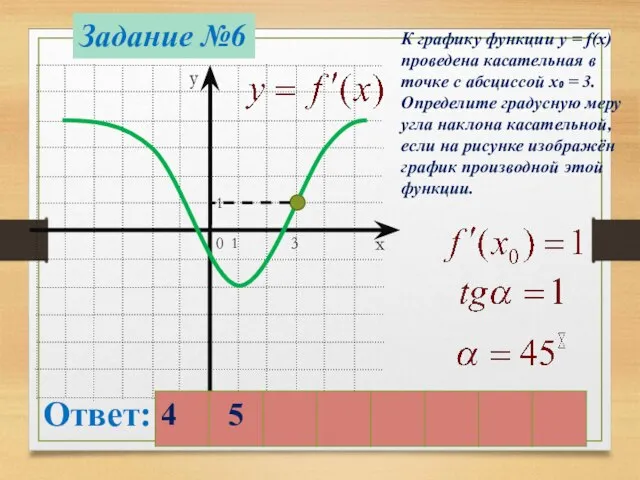
- 12. Задание №6 0 1 1 3 К графику функции y = f(x) проведена касательная в точке
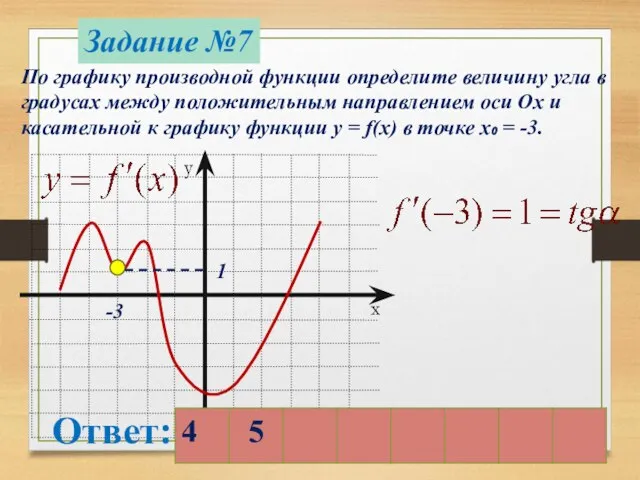
- 13. Задание №7 По графику производной функции определите величину угла в градусах между положительным направлением оси Ох
- 14. Задание №8 Задание №9 Ответ: Ответ: подсказка подсказка
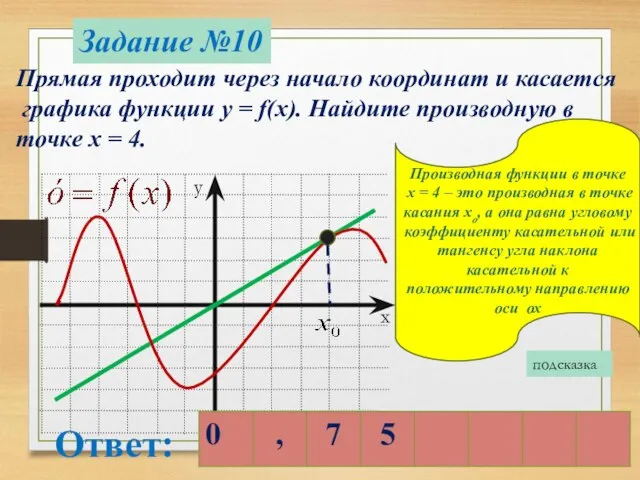
- 15. Производная функции в точке х = 4 – это производная в точке касания хо, а она
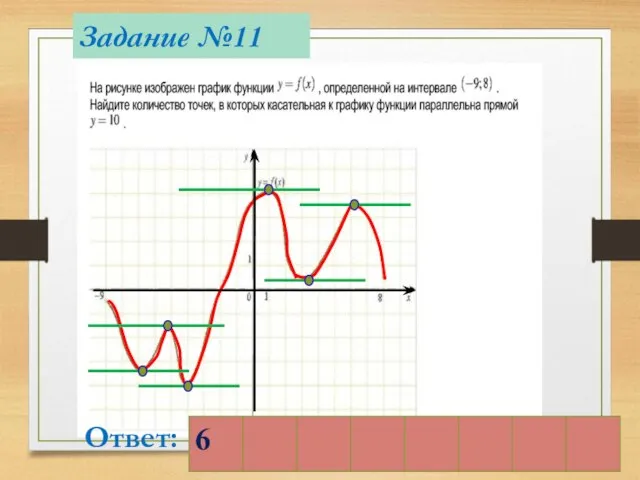
- 16. Задание №11 Ответ:
- 17. Решите самостоятельно следующие задания
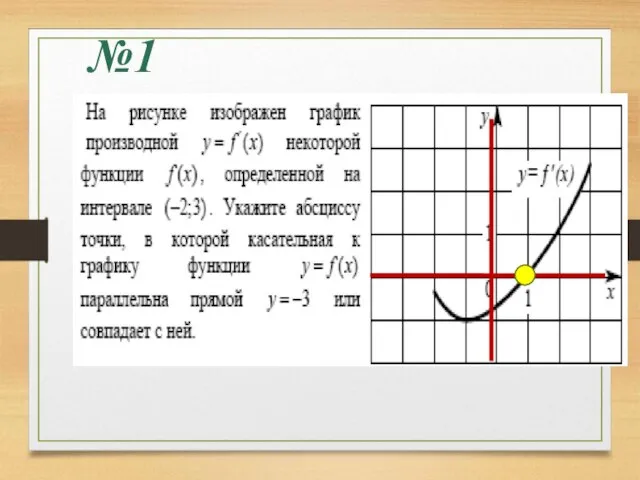
- 18. №1
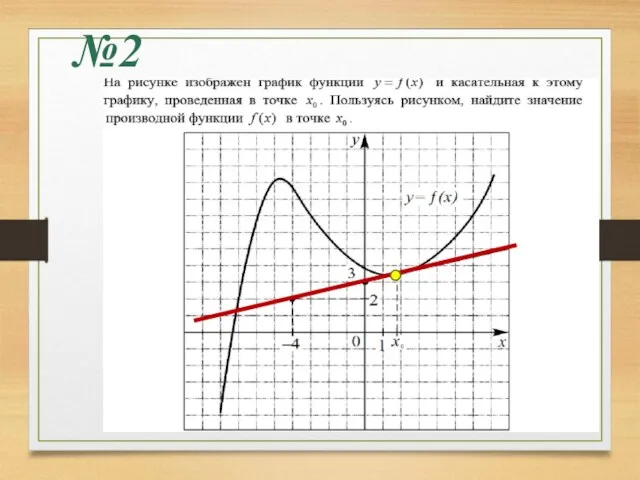
- 19. №2
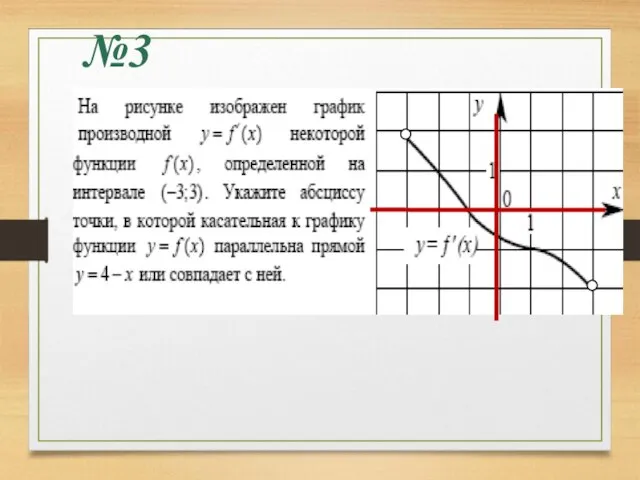
- 20. №3
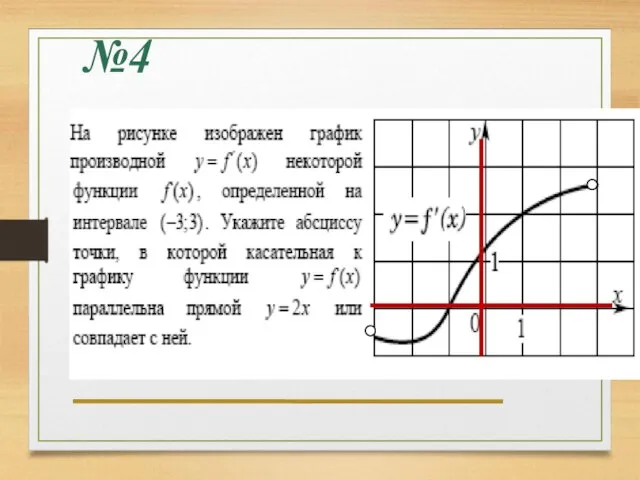
- 21. №4
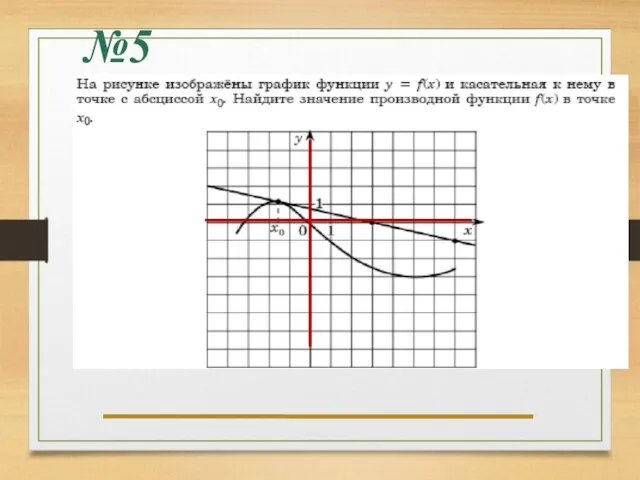
- 22. №5
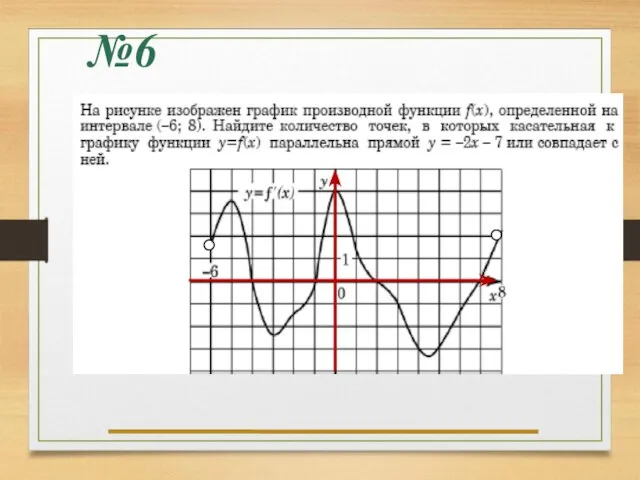
- 23. №6
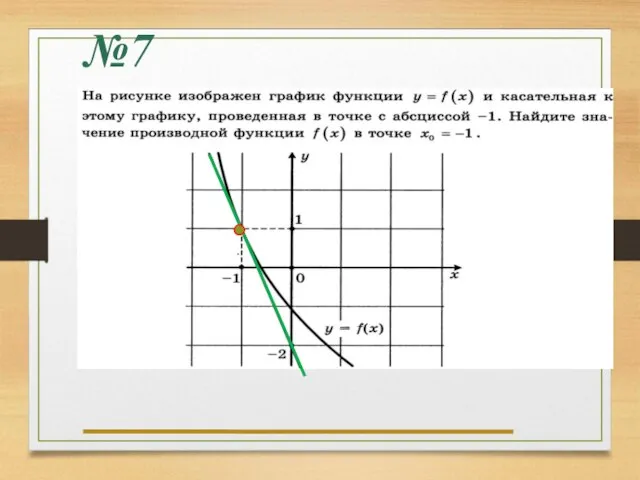
- 24. №7
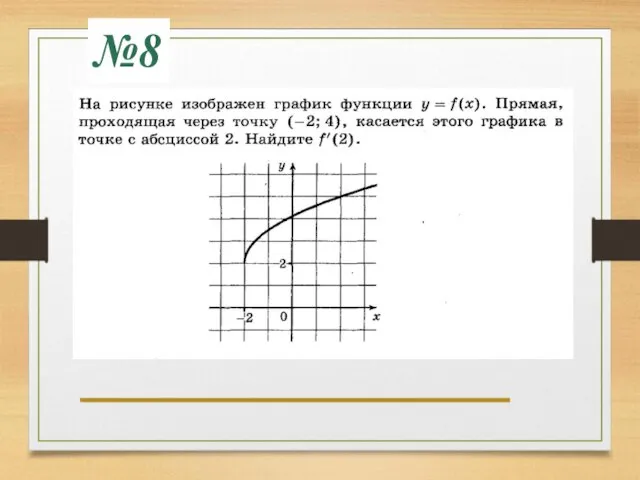
- 25. №8
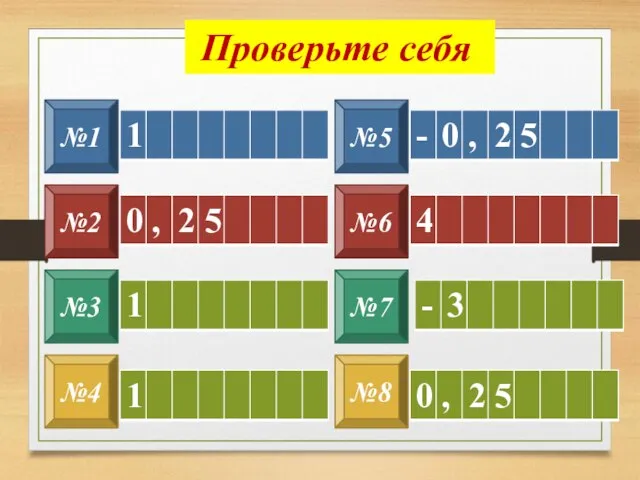
- 26. №1 №2 №3 №4 №8 №7 №6 №5 Проверьте себя
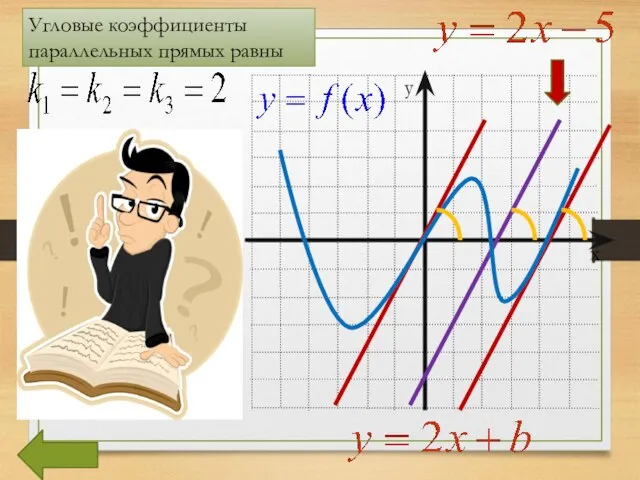
- 27. Угловые коэффициенты параллельных прямых равны
- 28. Для вычисления углового коэффициента касательной достаточно найти отрезок касательной с концами в вершинах клеток и, считая
- 29. Так как касательная параллельна прямой y=8x+11, то их угловые коэффициенты совпадают, т.е. угловой коэффициент касательной равен
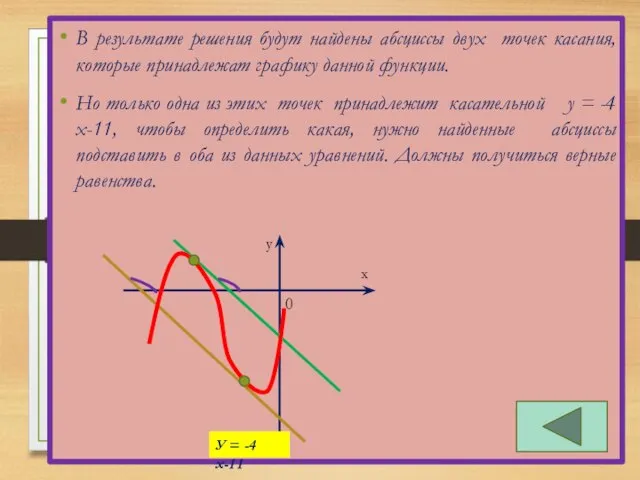
- 30. В результате решения будут найдены абсциссы двух точек касания, которые принадлежат графику данной функции. Но только
- 31. Памятка Чтобы найти угловой коэффициент касательной к графику функции в заданной точке или значение производной функции
- 32. Ну кто придумал эту математику ! У меня всё получилось!!! Надо решить ещё пару примеров. Рефлексия
- 34. Скачать презентацию








 Презентация по математике "Ломаные числа" -
Презентация по математике "Ломаные числа" -  Умножение числа 0 и на число 0 Умножение числа 1 и на число 1
Умножение числа 0 и на число 0 Умножение числа 1 и на число 1 Методы корреляционно-регрессионного анализа фондового рынка
Методы корреляционно-регрессионного анализа фондового рынка Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Математика и техника. Их связь и значение
Математика и техника. Их связь и значение Групповое задание
Групповое задание Коррекция нелинейных систем
Коррекция нелинейных систем Перемещение тела на плоскости (задача)
Перемещение тела на плоскости (задача) Теорема Пифагора
Теорема Пифагора Таблица умножения на 2
Таблица умножения на 2 Повторение и закрепление. Итоговое повторение за год. 4 класс
Повторение и закрепление. Итоговое повторение за год. 4 класс Прямоугольник. Ромб. Квадрат
Прямоугольник. Ромб. Квадрат Что такое разложение на множители и зачем оно нужно
Что такое разложение на множители и зачем оно нужно Гомотетия. Подобие фигур
Гомотетия. Подобие фигур Элементы математической логики
Элементы математической логики История возникновения науки геометрии
История возникновения науки геометрии Презентация на тему Окружность ее центр и радиус
Презентация на тему Окружность ее центр и радиус  Геометрические тела. 9 класс
Геометрические тела. 9 класс Формирование регулятивных УУД у младших школьников при изучении геометрического материала
Формирование регулятивных УУД у младших школьников при изучении геометрического материала Стандартизация в различных сферах. Сущность стандартизации
Стандартизация в различных сферах. Сущность стандартизации Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Kоординатная плоскость
Kоординатная плоскость Средние величины
Средние величины Математика. Роль математики в жизни людей и общества
Математика. Роль математики в жизни людей и общества Действия с натуральными числами. Сложение и вычитание
Действия с натуральными числами. Сложение и вычитание Решение уравнений
Решение уравнений Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)