Содержание
- 2. Лекция № 10 Непрерывность функций Учебные вопросы: В1. Непрерывность функций в точке и на множестве. В2.
- 3. Лекция № 10 Непрерывность функций В1. Непрерывность функций в точке и на множестве.
- 4. Лекция № 10 Непрерывность функций В1. Непрерывность функций в точке и на множестве. Определение 1. Функция
- 5. Лекция № 10 Непрерывность функций Определение 2. Если f(x) – непрерывна ∀х∈Х, то говорят, что она
- 6. Лекция № 10 Непрерывность функций Теорема 1. Для того, чтобы необходимо и достаточно, чтобы бесконечно малому
- 7. Лекция № 10 Непрерывность функций Пример 1. Исследовать функцию у=х на непрерывность. Пример 2. Исследовать функцию
- 8. Лекция № 10 Непрерывность функций
- 9. Лекция № 10 Непрерывность функций
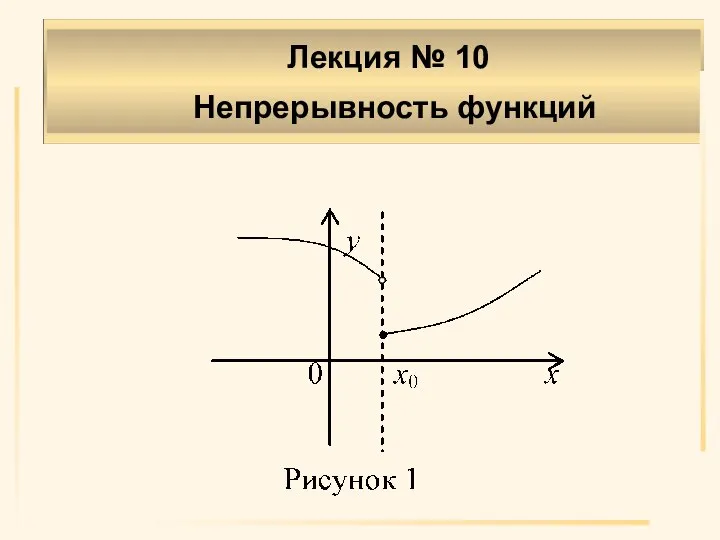
- 10. Лекция № 10 Непрерывность функций Определение 3. Функция f(x) - непрерывна в точке х0, если она
- 11. В2. Свойства непрерывных функций Теорема 2. Если U(x), V(x) непрерывны в точке х0, то функции U±V,
- 12. Теорема 3. Если функция f(u) непрерывна в точке u0, а функция u=φ(x) – непрерывна в точке
- 13. Теорема 4. Основные элементарные функции (степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрическим) непрерывны в своей области определения.
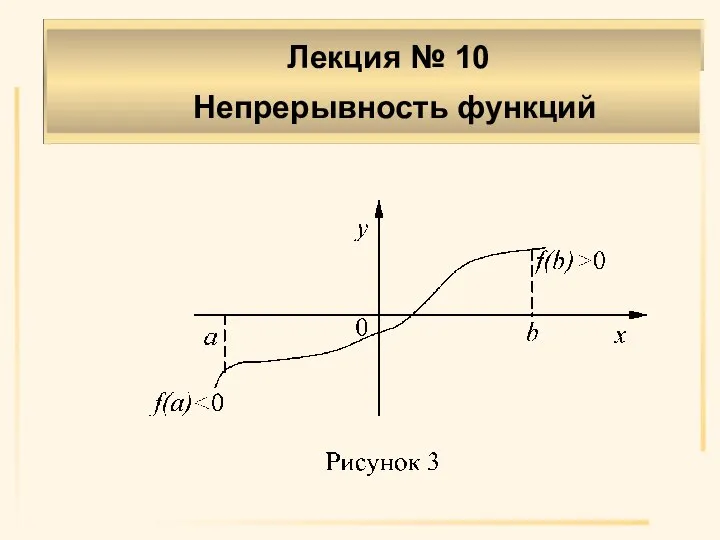
- 14. Свойства функций непрерывных на отрезке Теорема 5 (Больцано-Коши). Пусть функция f(x) определена и непрерывна в замкнутом
- 15. Лекция № 10 Непрерывность функций
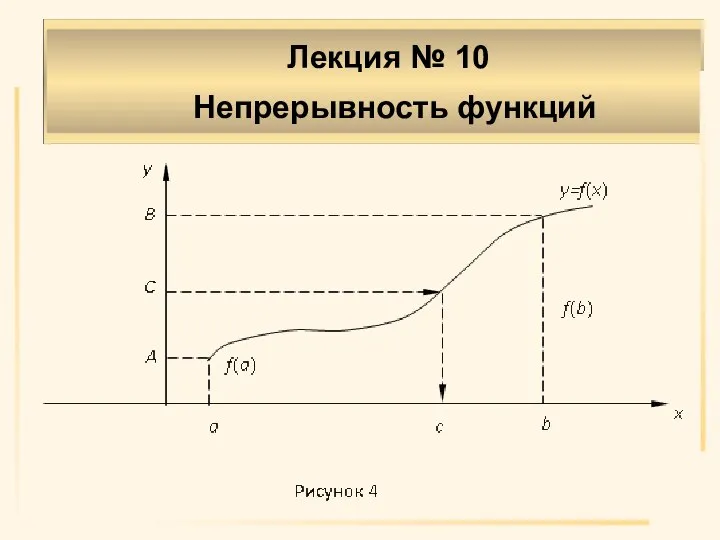
- 16. Теорема 6 (о промежуточных значениях). Если функция f(x) определена и непрерывна в замкнутом промежутке [a,b] и
- 17. Лекция № 10 Непрерывность функций
- 18. Теорема 7. (Первая теорема Вейерштрасса) Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке
- 19. Теорема 8 (Вторая теорема Вейерштрасса). Если функция f(x) определена и непрерывна в замкнутом промежутке [a,b], то
- 20. В3. Классификация точек разрыва функции Определение 4. Точкой разрыва функции f(x) называется точка x0, в которой
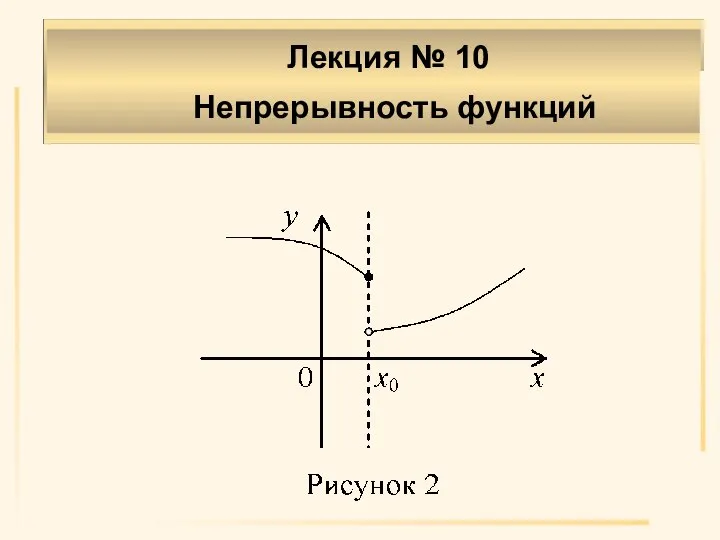
- 21. Определение 5. Если у функции f(x) в точке x0 существуют конечные левый и правый пределы f(x0–0),
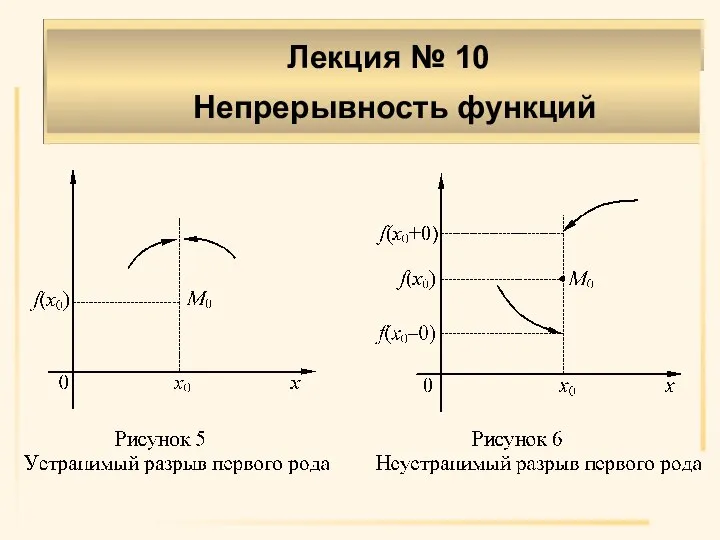
- 22. Определение 6. Если в x0 разрыв первого рода и f(x0–0)=f(x0+0)≠f(x0) либо f(x0–0)=f(x0+0), а f(x0) не существует,
- 23. Определение 7. Если в x0 разрыв первого рода и f(x0–0)≠f(x0+0), то разрыв называется неустранимым разрывом первого
- 24. Лекция № 10 Непрерывность функций
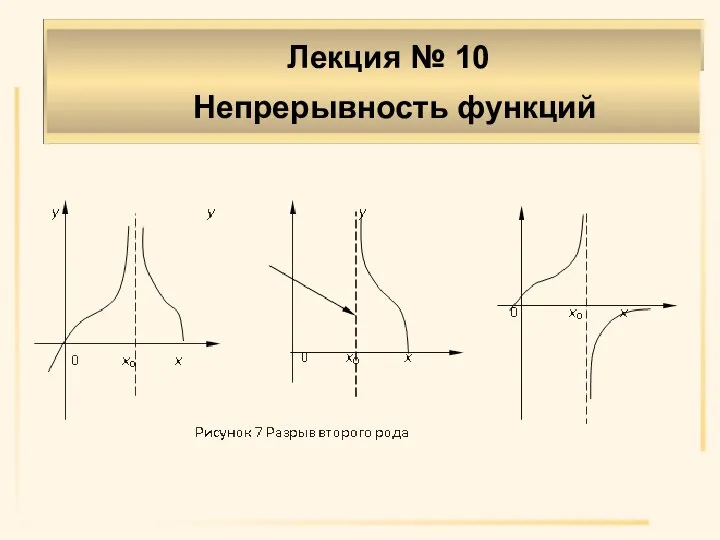
- 25. Определение 8. Если не существует хотя бы один из односторонних пределов функции f(x0–0), f(x0+0) или хотя
- 26. Лекция № 10 Непрерывность функций
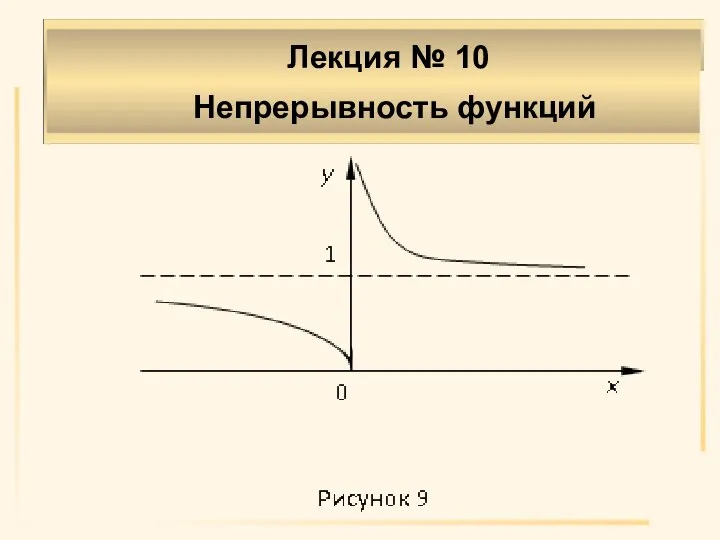
- 27. Пример. Исследовать функцию (a>1) на непрерывность. Лекция № 10 Непрерывность функций
- 28. Лекция № 10 Непрерывность функций
- 30. Скачать презентацию




















 ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ»
ПРОЕКТ «КАК ИЗМЕРЯЛИ В СТАРИНУ» Решение задач
Решение задач Периметр прямоугольника. Площадь прямоугольника. Путь. (5 класс)
Периметр прямоугольника. Площадь прямоугольника. Путь. (5 класс) В мире плоскостей
В мире плоскостей Решение задач. 6 класс
Решение задач. 6 класс Треугольник и его элементы
Треугольник и его элементы Игра Верю - не верю
Игра Верю - не верю Перспективная модель ЕГЭ по математике
Перспективная модель ЕГЭ по математике Математическое путешествие в мир гармонии. Устный журнал
Математическое путешествие в мир гармонии. Устный журнал Живая планета!
Живая планета! Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Числовые промежутки
Числовые промежутки Презентация на тему Функция у=х^2, её свойства и график
Презентация на тему Функция у=х^2, её свойства и график  Распределение случайных величин. Функция распределения и плотность распределения случайной величины
Распределение случайных величин. Функция распределения и плотность распределения случайной величины Осевая и центральная симметрия
Осевая и центральная симметрия Радианная Мера Угла
Радианная Мера Угла Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани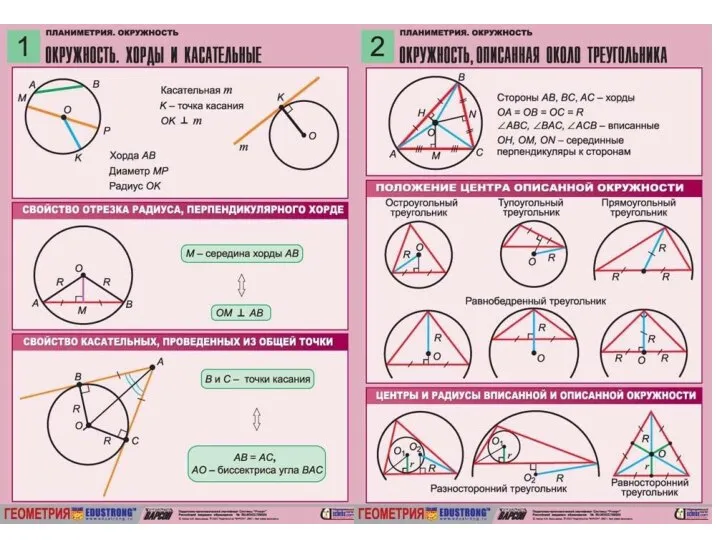 Геометрия. Конспекты
Геометрия. Конспекты Интегральное исчисление. Первообразная функция. Неопределённый интеграл
Интегральное исчисление. Первообразная функция. Неопределённый интеграл Ребуси Вавіліної Анастасії
Ребуси Вавіліної Анастасії Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Презентация на тему Решение задач на нахождение неизвестного по двум разностям
Презентация на тему Решение задач на нахождение неизвестного по двум разностям  Теория погрешностей
Теория погрешностей Треугольники. Решение задач
Треугольники. Решение задач Определение неизвестного числа
Определение неизвестного числа Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Станция логическая. По тропинкам занимательной математики
Станция логическая. По тропинкам занимательной математики Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики
Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики