Лекция 2

B = A([1 3 2], :) – меняет местами 2-ю и 3-ю строку матрицы A;
B = A(:, [1 3 2]) – меняет местами 2-й и 3-й столбец матрицы A;
P= [A C] – конкатенация (объединение) матриц в ширину
Q=[A ; C] – объединение матриц в высоту
A*B – умножение матриц; A.*B – поэлементное умножение матриц;
A^2 – умножение матриц A*A; A.^2– поэлементное возведение
квадрат;
A/B – деление слева направо, эквивалентно A*B^-1
A\B – деление справа налево, эквивалентно A^-1*B
[A B] – объединение матриц (совпадение по строкам)
[A; B] – объединение матриц (совпадение по столбцам)
zeros(n,m) – создаёт массив n*m, заполненный нулями
ones(n,m) – создаёт массив n*m, заполненный единицами
eye(n,n) – формирует единичную матрицу n*n

rand(n, m) – создаёт матрицу n*m со случайными элементами, распределёнными по равномерному закону в (0,1)
max(A) – находит максимальные элементы в матрице A
[C,I]=max(A) – возвращает максимальный элемент в столбце (C) и номер строки (I), в которой он находится
Аналогично min(A)
sum(A) – сумма элементов матрицы
Аналогично prod(A) – произведение
diag(A) – возвращает главную диагональ матрицы A
det(A) – возвращает определитель матрицы A
trace(A) – возвращает след матрицы A
inv(A) – возвращает обратную матрицу

Задана система линейных алгебраических уравнений (СЛАУ):
n уравнений
n неизвестных
вида:
Решение СЛАУ методом обратной матрицы

Другое описание: A · x = b,
где x — вектор неизвестных,
A — матрица коэффициентов при неизвестных или матрица системы,
b — вектор свободных членов системы.
Матричный метод (метод обратной матрицы):
если задано Ax=B,
то
x=A\B;
x=A-1*B;
x=inv(A)*B ;
Пример:
Результат:
5.
-3.331D-16
-5.
4.441D-16

Решение СЛАУ методом Жордана-Гаусса
Метод Жордана-Гаусса:
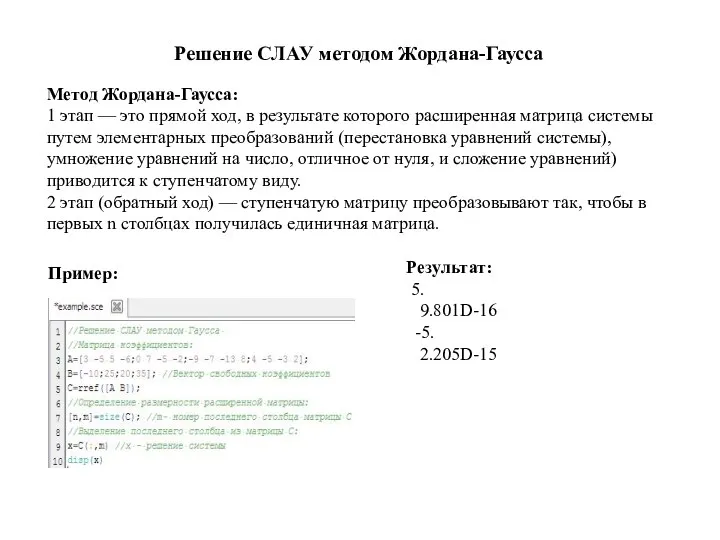
1 этап — это прямой ход, в результате которого расширенная матрица системы путем элементарных преобразований (перестановка уравнений системы), умножение уравнений на число, отличное от нуля, и сложение уравнений) приводится к ступенчатому виду.
2 этап (обратный ход) — ступенчатую матрицу преобразовывают так, чтобы в первых n столбцах получилась единичная матрица.
Пример:
Результат:
5.
9.801D-16
-5.
2.205D-15