Содержание
- 2. Правило произведения Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций,
- 3. Перестановками из n элементов называются соединения (комбинации), которые состоят из одних и тех же n элементов
- 4. Число перестановок: (1) Произведение первых n натуральных чисел обозначают n! (читается «эн факториал») n! = 1⋅2⋅3⋅...⋅(n
- 5. Размещениями из m элементов по n элементов (n ≤ m) называются такие соединения, каждое из которых
- 6. = m(m – 1)(m – 2) • … • (m – (n – 1)) = 4
- 7. Сочетаниями из m элементов по n в каждом (n≤m) называются соединения, каждое из которых содержит n
- 8. Образуем все соединения, содержащие n элементов, выбранных из данных m разных элементов, без учета порядка их
- 11. Скачать презентацию







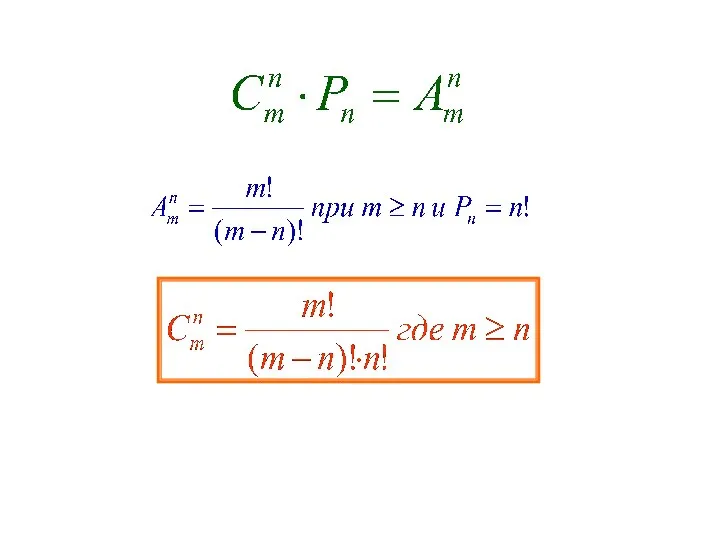
 Знаки +, -, =. Прибавить, вычесть, получится
Знаки +, -, =. Прибавить, вычесть, получится Подобие треугольников. Применение подобия к решению задач
Подобие треугольников. Применение подобия к решению задач Преобразование графиков функций. 9 класс
Преобразование графиков функций. 9 класс Многогранники
Многогранники Презентация на тему Элементы математической логики
Презентация на тему Элементы математической логики  Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Векторы в пространстве. Практическая работа
Векторы в пространстве. Практическая работа Луч и угол
Луч и угол Вычитание векторов
Вычитание векторов Metode numerice
Metode numerice Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)
Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)  Логические задачи. Математика и информатика. Тетрадь для 1–2 классов
Логические задачи. Математика и информатика. Тетрадь для 1–2 классов Векторы плоскости
Векторы плоскости Концентрация кислоты
Концентрация кислоты Презентация на тему Преобразования фигур в пространстве
Презентация на тему Преобразования фигур в пространстве  7badff53-fae3-4f94-8d75-de14f449e5f4
7badff53-fae3-4f94-8d75-de14f449e5f4 Мир чисел
Мир чисел Сложение смешанных дробей
Сложение смешанных дробей Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля
Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля предел_числ_посл
предел_числ_посл Первый признак равенства треугольников. Теорема
Первый признак равенства треугольников. Теорема Презентация на тему Математика 3 класс Виды треугольников
Презентация на тему Математика 3 класс Виды треугольников  Разметка прямоугольника по угольнику
Разметка прямоугольника по угольнику Системы принятия решений
Системы принятия решений Путешествие в страну дроби
Путешествие в страну дроби Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Презентация на тему Методы решения иррациональных уравнений
Презентация на тему Методы решения иррациональных уравнений  Математическая статистика. Лекция 1
Математическая статистика. Лекция 1